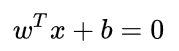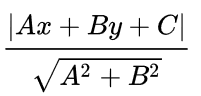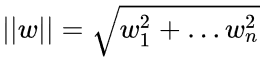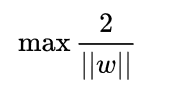数据挖掘算法和实践（四）：支持向量机（iris鸢尾花数据集）
支持向量机同样是一种分类算法，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，当训练样本线性可分时，通过硬间隔最大化学习一个线性可分支持向量机；当训练样本近似线性可分时，通过软间隔最大化学习一个线性支持向量机；当训练样本线性不可分时，通过核技巧和软间隔最大化学习一个非线性支持向量机，该算法思路比较简单，但推导过程比较复杂，需要高等数学知识；
算法优点：① 纯高等数学知识思维，可解释性强，不依靠统计方法，从而简化了通常的分类和回归问题；② 采用核技巧之后，可以处理非线性分类/回归任务；③ 最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了“维数灾难”
算法缺陷：① 训练时间长，时间复杂度
；② 当采用核技巧时，如果需要存储核矩阵，则空间复杂度为 ；③ 预测时间与支持向量的个数成正比，当支持向量的数量较大时，预测计算复杂度较高。
线性可分
如果一个线性函数（二维空间中的直线）能够将样本分开，称这些数据样本是线性可分的，在三维空间是一个平面，以此类推，如果不考虑空间维数，这样的线性函数统称为超平面，通常我们所说的线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。
SVM最优化问题
SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述：
点(x,y)到
的距离公式为：
扩展到 n 维空间后，点x=(x1,x2,x3,x4.....xn)到直线
的距离为：
其中:
经过推导我们的优化问题是：
再做一个转换，为了方便计算（去除
的根号），得到的最优化问题是：
拉格朗日乘法
可以使用本科高等数学学的拉格朗日程数法是等式约束优化问题思想，构造拉格朗日函数：
核函数
我们可能会碰到的一种情况是样本点不是线性可分的，这种情况的解决方法就是：将二维线性不可分样本映射到高维空间中，让样本点在高维空间线性可分，对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。
用法
sklearn提供了三种基于svm的分类方法：
sklearn.svm.NuSVC()
sklearn.svm.LinearSVC()
sklearn.svm.SVC()
其中用得最多的是 sklearn.svm.SVC()，全称是C-Support Vector Classification，是一种基于libsvm的支持向量机，由于其时间复杂度为O(n^2)，所以当样本数量超过两万时难以实现。
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True,
probability=False, tol=0.001, cache_size=200, class_weight=None,
verbose=False, max_iter=-1, decision_function_shape='ovr',
random_state=None)
- 相关参数
- C （float参数 默认值为1.0）
表示错误项的惩罚系数C越大，即对分错样本的惩罚程度越大，因此在训练样本中准确率越高，但是泛化能力降低；相反，减小C的话，容许训练样本中有一些误分类错误样本，泛化能力强。对于训练样本带有噪声的情况，一般采用后者，把训练样本集中错误分类的样本作为噪声。 - kernel （str参数 默认为‘rbf’）
该参数用于选择模型所使用的核函数，算法中常用的核函数有：
-- linear：线性核函数
-- poly：多项式核函数
--rbf：径像核函数/高斯核
--sigmod：sigmod核函数
--precomputed：核矩阵，该矩阵表示自己事先计算好的，输入后算法内部将使用你提供的矩阵进行计算 - degree （int型参数 默认为3）
该参数只对'kernel=poly'(多项式核函数)有用，是指多项式核函数的阶数n，如果给的核函数参数是其他核函数，则会自动忽略该参数。 - gamma （float参数 默认为auto）
该参数为核函数系数，只对‘rbf’,‘poly’,‘sigmod’有效。如果gamma设置为auto，代表其值为样本特征数的倒数，即1/n_features，也有其他值可设定。 - coef0:（float参数 默认为0.0）
该参数表示核函数中的独立项，只有对‘poly’和‘sigmod’核函数有用，是指其中的参数c。 - probability（ bool参数 默认为False）
该参数表示是否启用概率估计。 这必须在调用fit()之前启用，并且会使fit()方法速度变慢。 - shrinkintol: float参数 默认为1e^-3g（bool参数 默认为True）
该参数表示是否选用启发式收缩方式。 - tol（ float参数 默认为1e^-3）
svm停止训练的误差精度，也即阈值。 - cache_size（float参数 默认为200）
该参数表示指定训练所需要的内存，以MB为单位，默认为200MB。 - class_weight（字典类型或者‘balance’字符串。默认为None）
该参数表示给每个类别分别设置不同的惩罚参数C，如果没有给，则会给所有类别都给C=1，即前面参数指出的参数C。如果给定参数‘balance’，则使用y的值自动调整与输入数据中的类频率成反比的权重。 - verbose （ bool参数 默认为False）
该参数表示是否启用详细输出。此设置利用libsvm中的每个进程运行时设置，如果启用，可能无法在多线程上下文中正常工作。一般情况都设为False，不用管它。 - max_iter （int参数 默认为-1）
该参数表示最大迭代次数，如果设置为-1则表示不受限制。 - random_state（int，RandomState instance ，None 默认为None）
该参数表示在混洗数据时所使用的伪随机数发生器的种子，如果选int，则为随机数生成器种子；如果选RandomState instance，则为随机数生成器；如果选None,则随机数生成器使用的是np.random。
from sklearn import svm
from sklearn import datasets
from sklearn.model_selection import train_test_split as ts
#import our data
iris = datasets.load_iris()
X = iris.data
y = iris.target
#split the data to 7:3
X_train,X_test,y_train,y_test = ts(X,y,test_size=0.3)
# select different type of kernel function and compare the score
# kernel = 'rbf'
clf_rbf = svm.SVC(kernel='rbf')
clf_rbf.fit(X_train,y_train)
score_rbf = clf_rbf.score(X_test,y_test)
print("The score of rbf is : %f"%score_rbf)
# kernel = 'linear'
clf_linear = svm.SVC(kernel='linear')
clf_linear.fit(X_train,y_train)
score_linear = clf_linear.score(X_test,y_test)
print("The score of linear is : %f"%score_linear)
# kernel = 'poly'
clf_poly = svm.SVC(kernel='poly')
clf_poly.fit(X_train,y_train)
score_poly = clf_poly.score(X_test,y_test)
print("The score of poly is : %f"%score_poly)- 方法
- svc.decision_function(X)
样本X到分离超平面的距离 - svc.fit(X, y[, sample_weight])
根据给定的训练数据拟合SVM模型。 - svc.get_params([deep])
获取此估算器的参数并以字典行书储存,默认deep=True，以分类iris数据集为例，得到的参数如下; - svc.predict(X)
根据测试数据集进行预测 - svc.score(X, y[, sample_weight])
返回给定测试数据和标签的平均精确度 - svc.predict_log_proba(X_test)，svc.predict_proba(X_test)
当sklearn.svm.SVC(probability=True)时，才会有这两个值，分别得到样本的对数概率以及普通概率。