2015-CVPR-Direction Matters_ Depth Estimation with a Surface Normal Classifier

2015-CVPR-Direction Matters: Depth Estimation with a Surface Normal Classifier

abstract

• 用分类器对整个集合法向量进行分类，通过一系列优化最终决定surface orientation(表面方向）

introduciton

• 用双目矫正图片对学习视差的局限性：
  
  • 条纹少的地方，如墙
  • 过度曝光的地方
  • 输入数据本身就很模糊，如反射地面
• 目前处理以上问题的方案：
  
  • 将基于不相似计算的匹配成本加入到最后的能量函数中
  • 利用图片中的边缘信息和先验知识，如平面表面
• 机器学习的引入使得分类器能够基于单张图片估计表面方向
• 本文的亮点：
  
  • 表面法向量估计对均匀的区域（墙，反射地面）的深度估计比较可靠
  • 不限制每个像素点只有一个法向量，多个法向量的存在能够解决分类器在某个方向不能可靠的推断视差的问题

related work

• Markov random field（MRF）：全局最优解决方案
• anisotropic Total Variation(TV) ：将图像中的边缘信息和深度不连续性联合起来

formulation

• 基于2D图片获取深度信息的能量函数最小化的问题，由于问题（给一个像素打上什么标记最优）非凸，全局energy函数一般是非凸问题，不过可以把问题转化为3D体素，一般都可以得到全局最优
• 三个知识点:
  
  • 前向差分离散化( forward difference discretization)
    
  • positively 1-homogeneous function
    
    • wiki
    • homogeneous function of degree 1: f(ax)=af(x) f ( a x ) = a f ( x )
    • 结论: f(ax)=af(x),a>0 f ( a x ) = a f ( x ) , a > 0 具有的性质: f(x)=x▿f(x) f ( x ) = x ▽ f ( x )
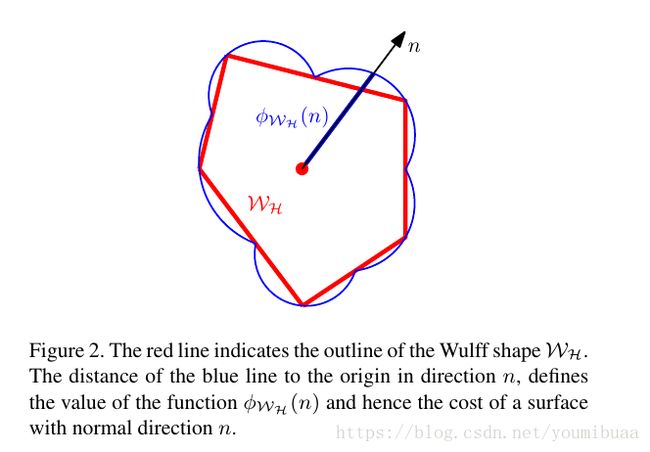
  • Wulff construction
    
    • wiki
    • 定义:体积一定的滴状或晶体达到平衡时的形状,能量(吉布斯自由能)最小化准则会选择晶体每个面的最佳形状
    • △Gi=∑jγjOj △ G i = ∑ j γ j O j , γj γ j 表示平面每单位面积的吉布斯自由能, Oj O j 表示每个平面的面积, △Gi △ G i 表示实际的晶体形状和用Wulff construction出来的晶体之间能量的差值
    • 晶体表面法向量的长度和平面能量的大小成正比,法向量是指从晶体的中心到平面的距离,对于一个球体而言就是它的半径.

能量函数公式:

对于图片 I=w∗h I = w ∗ h 中的任意像素点 (r,s) ( r , s ) ,其标记 ℓ(r,s)∈ ℓ ( r , s ) ∈ L ={0,…,L} = { 0 , … , L } .那么引入变量 u(r,s,t)∈[0,1] u ( r , s , t ) ∈ [ 0 , 1 ] ,对任意 (r,s,t)∈Ω=I∗L ( r , s , t ) ∈ Ω = I ∗ L 成立.

u(r,s,t)={01if ℓ(r,s)<telse u ( r , s , t ) = { 0 if  ℓ ( r , s ) < t 1 else

这相当于在 Ω Ω 立体空间找到一个分割面,在边界上添加规则化项和限制,使得标记分配问题变成一个凸优化问题

那么能量函数表达式如下:

E(u)=∑r,s,t{ρ(r,s,t)|(▿tu)(r,s,t)|+ϕ(r,s,t)(▿u)(r,s,t)}s.t.u(r,s,0)=0u(r,s,L)=1∀(r,s) E ( u ) = ∑ r , s , t { ρ ( r , s , t ) | ( ▽ t u ) ( r , s , t ) | + ϕ ( r , s , t ) ( ▽ u ) ( r , s , t ) } s . t . u ( r , s , 0 ) = 0 u ( r , s , L ) = 1 ∀ ( r , s )

其中:
1. ρ(r,s,t)为给像素(r,s)分配标记t的 ρ ( r , s , t ) 为 给 像 素 ( r , s ) 分 配 标 记 t 的 data costs, ▿t ▽ t 表示对标记维t进行求导, ▿ ▽ 表示对所有维度进行求导.两种求导方式都用 前向差分离散化替代.
2. 而 ϕ(r,s,t) ϕ ( r , s , t ) 可以是任意 convex positively 1-homogeneous function,效果是对cut surface 进行anisotropic peneliazation(各向异性惩罚),并且这个规则化项是依据法向量方向分类器来定义的.
3. 分类器会对每个像素 (r,s) ( r , s ) 和离散的平面法向量集合 n n 输出一个分数 k(r,s,n) k ( r , s , n ) ,为了充分利用这个分数,惩罚项是各向异性的,那么就会选出平面的最佳法向量

---

不过,以上条件一般很难满足,所以可以通过构建一个凸包形状来代替,Wulff shape就是一个凸的,封闭的,有界的集合,并且包含原点(法向量所在的点).
构建Wulff shape思想:半空间(half space)相交.对于一个离散的半空间集合 H H ,法向量朝外,包含原点,且原点到边界的距离为 dn d n .从这个集合中选取用来构建Wulff shape 的子集为 WH W H .

ϕw(▿u)=maxp∈WpT▿u⟶ϕWH(n)=maxp∈WHpTn=dn,dnr=k(r,s,n) ϕ w ( ▽ u ) = max p ∈ W p T ▽ u ⟶ ϕ W H ( n ) = max p ∈ W H p T n = d n , d r n = k ( r , s , n )

Transforming the Normal Directions

• 法向量转换: 把法向矢量看作是矢量(法向量)而不是垂直于它们的平面，让 v v 和 n n 是矢量，使得 v v 垂直于 n n 。那么 nTv=0 n T v = 0 。因此，对于任意非奇异变换 M M ， nTM−1Mv=0 n T M − 1 M v = 0 ，这意味着 nTM−1 n T M − 1 是变换的法向量的转置。因此，变换的法向矢量是 (M−1)Tn ( M − 1 ) T n 。换句话说，法向量由变换点的变换的逆转置来变换。
  
  the transfromation of normal direction:N=(M−1)T the transfromation of normal direction : N = ( M − 1 ) T
• 相机图像帧与世界坐标系之间的转换关系
• 雅克比矩阵
• 下面将对binocular stereo的法向量转换进行分析:
  
  • 对于图像上的点 (r,s) ( r , s ) ,视差值为 t t ,即(r,s,t);和世界坐标系中物体坐标(x,y,z),转换关系如下:
    
    ⎛⎝⎜⎜rst⎞⎠⎟⎟=⎛⎝⎜⎜⎜fxxz+cxfyyz+cybfxz⎞⎠⎟⎟⎟ ( r s t ) = ( f x x z + c x f y y z + c y b f x z )
  • 上面是世界坐标系转换为视差空间的关系矩阵,对该矩阵求雅克比矩阵
    
    J(x,y,z)=⎛⎝⎜⎜⎜⎜fxz000fyz0−xfxz2−yfyz2−bfxz2⎞⎠⎟⎟⎟⎟ J ( x , y , z ) = ( f x z 0 − x f x z 2 0 f y z − y f y z 2 0 0 − b f x z 2 )
  • 即求得视差空间中某点处切平面的方向,那么世界坐标系vector变换到视差空间vector的关系矩阵记为 M=J(x,y,z) M = J ( x , y , z ) ,那么normal法向量的变换矩阵为 N=(M−1)T N = ( M − 1 ) T
  • 法向量转换矩阵:
    
    N=⎛⎝⎜⎜⎜⎜zfx0−xzbfx0zfy−zybfx00−z2bfx⎞⎠⎟⎟⎟⎟M=(NT)−1⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯MT×N=E N = ( z f x 0 0 0 z f y 0 − x z b f x − z y b f x − z 2 b f x ) M = ( N T ) − 1 _ M T × N = E
    
    对于上面两个M矩阵之间的差异,我也没找到好的解释,欢迎大家留言讨论!
    本来是没有求雅克比矩阵,直接把空间点坐标变换当成 M M 矩阵,然后死活不知道 M M 变换到 N N 的,后来经过实验室数学系大佬orz的指点推导,发现没有求雅克比矩阵.其实也对,不同space间点坐标变换和向量变换的确是不一样的,normal法向量和切平面向量才是有对应关系的,所以求雅克比矩阵求得切平面向量才应该是正解.
    还是应了那句话:数学即真理!!!orz

final optimization problem

• 对法向量 n n 的分类划分是基于训练数据的聚类.因为不能对每个方向进行采样,所以在半空间交界处会出现long thin corners问题,解决方法是:将Wulff shape和单位球 B3 B 3 (包含内部)相交,从而限制对long thin coreners的过度惩罚. 当然也需要对所有的分数进行归一化.
• 将边缘信息加入到规则化项可以让分类器处理不了的梯度不连续处的法向量方向被处理.而梯度不连续的地方的法向量方向一般和图片梯度方向或者负方向对齐.通过公式 k=k1+k2e−∥▿I∥k3 k = k 1 + k 2 e − ∥ ▽ I ∥ k 3 将这种情况加入到Wulff shape中

那么,最终的优化目标是:
拉格朗日乘子 η η 强调 p和q p 和 q 的一致性;energy可以通过 u u 和 η η 极小化,通过 p p 和 q q 最大化.算法在primal项单调减,在dual项单调升.

E(u,η,p,q)=∑r{ρr|(▿tu)r|+pTr(▿u)r+ηTr(pr−qr)}subject tou(r,s,0)=0,u(r,s,L)=1,∀(r,s)pr∈WHr,qr∈B3,∀r E ( u , η , p , q ) = ∑ r { ρ r | ( ▽ t u ) r | + p r T ( ▽ u ) r + η r T ( p r − q r ) } subject to u ( r , s , 0 ) = 0 , u ( r , s , L ) = 1 , ∀ ( r , s ) p r ∈ W H r , q r ∈ B 3 , ∀ r

Implementation

• Census transformation
• 2014-ECCV-Discriminatively trained dense surface normal estimation
  
  • 结合上下文信息和分割信息,提取图像特征
  • 用5000个弱分类器集成学习,合成一个强分类器.对surface normal 进行预测
  • 对标签空间的编码:
    
    1. 用k-means对法向量的ground-truth聚类,并且在每次投影都把簇中心投影到单位(半)球.簇中心用参考向量 Nk N k 表示.
    2. 然后选择三个参考向量构建三角形T( {t1i,t2i,t3i} { t i 1 , t i 2 , t i 3 } ),并寻找每个ground-truth法向量 nj n j 对应的最近邻三角形 t(j) t ( j )
    3. 接着利用公式
       
       t(j)=argminti∈Tminαjti|nj−∑p=13αjtpiNtpi|∑p=13αjtpi=1,andαjtpi⩾0,∀p∈{1,2,3}⇒nj≈∑kαjkNk,αjk{>00if k=tpiotherwise t ( j ) = a r g m i n t i ∈ T m i n α t i j | n j − ∑ p = 1 3 α t i p j N t i p | ∑ p = 1 3 α t i p j = 1 , a n d α t i p j ⩾ 0 , ∀ p ∈ { 1 , 2 , 3 } ⇒ n j ≈ ∑ k α k j N k , α k j { > 0 if  k = t i p 0 otherwise
       
       用强分类器求解最近邻三角形 t(j) t ( j ) ,在 α α 尽量小的情况下求解最能表示 nj n j 的三角形 t(j) t ( j )
    4. 最后用三角形 t(j) t ( j ) 表示ground-truth 法向量 nj n j
• 法向量聚类为40个簇,法向量之间的相似性通过boosting regression(如adaboost,random forest)结合(contextual)上下文信息和超像素信息计算
• Contextual信息由4个密集的特征提取方法:texton, self-similarity, local quantized ternary pattern, SIFT.每个方法提取的特征合成512维的Bag of Words
• 无监督超像素分割由4个分割方法:MeanShift, SLIC, GraphCut-segmentation, normalized cuts
• 分类器对每个像素输出是簇中心法向量方向的40个分数.归一化[0,1].
• 然后通过上面求出的法向量转换矩阵 N N 对每个像素的法向量转换到3维 Ω Ω 空间
• 半平面相交处的法向量数值变化小,所以不用保留交界处所有位置的法向量信息.而且一般只有一个或者几个法向量的分数较高
• 对边缘信息也加入到规则化项(regularization)