BFS、DFS以及Dijkstra算法 python实现

注：全文参考正月点灯笼b站up主！！

BFS：广度优先搜索，队列，先进先出；

DFS：深度优先搜索，栈， 先进后出；

Dijkstra：最短路径问题；

1、BFS和DFS

graph = {
    "A" : ["B","C"],
    "B" : ["A","C","D"],
    "C" : ["A","B","D","E"],
    "D" : ["B","C","E","F"],
    "E" : ["C","D"],
    "F" : ["D"]
}

def BFS(graph, s):
    deque = [s]
    seen = set()
    seen.add(s)
    while deque:
        vertex = deque.pop(0)
        nodes = graph[vertex]
        for x in nodes:
            if x not in seen:
                deque.append(x)
                seen.add(x)
        print(vertex)

def DFS(graph, s):
    stack = [s]
    seen = set()
    seen.add(s)
    while stack:
        vertex = stack.pop()
        nodes = graph[vertex]
        for x in nodes:
            if x not in seen:
                stack.append(x)
                seen.add(x)
        print(vertex)

2、Dijkstra

import heapq
import math

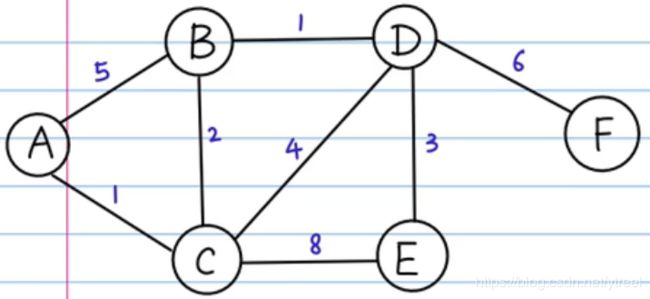
graph = {
    "A" : {"B":5, "C":1},
    "B" : {"A":5, "C":2, "D":1},
    "C" : {"A":1, "B":2, "D":4, "E":8},
    "D" : {"B":1, "C":4, "E":3 ,"F":6},
    "E" : {"C":8, "D":3},
    "F" : {"D":6}
}

def init_distance(graph, s):
    distance = {s:0}
    for x in graph.keys():
        if x != s:
            distance[x] = math.inf
    return distance

def Dijkstra(graph, s):
    pqueue = []
    heapq.heappush(pqueue, (0,s))
    seen = set()
    parent = {s:None}
    distance = init_distance(graph, s)
    while pqueue:
        pair = heapq.heappop(pqueue)
        dist   = pair[0]
        vertex = pair[1]
        seen.add(vertex)
        nodes = graph[vertex].keys()
        for x in nodes:
            if x not in seen:
                if dist + graph[vertex][x] < distance[x]:
                    heapq.heappush(pqueue, (dist + graph[vertex][x], x))
                    parent[x] = vertex
                    distance[x] = dist + graph[vertex][x]
    return parent, distance

parent, distance = Dijkstra(graph, "A")
print(parent)
print(distance)