斯坦福机器学习实现与分析之五（高斯判别分析）

斯坦福机器学习实现与分析之五（高斯判别分析）

http://www.cnblogs.com/jcchen1987/p/4424436.html

高斯判别分析（GDA）简介

---

　　首先，高斯判别分析的作用也是用于分类。对于两类样本，其服从伯努利分布，而对每个类中的样本，假定都服从高斯分布，则有:

y∼Bernouli(ϕ)

x|y=0∼N(μ0,Σ)

x|y=1∼N(μ1,Σ)

　　这样，根据训练样本，估计出先验概率以及高斯分布的均值和协方差矩阵（注意这里两类内部高斯分布的协方差矩阵相同），即可通过如下贝叶斯公式求出一个新样本分别属于两类的概率，进而可实现对该样本的分类。

　 p(y|x)=p(x|y)p(y)p(x)

y=argmaxyp(y|x)=argmaxyp(x|y)p(y)p(x)=argmaxyp(x|y)p(y)  

 

GDA详细推导

---

　　那么高斯判别分析的核心工作就是估计上述未知量 ϕ,μ0,μ1,Σ 。如何来估计这些参数？又该最大似然估计上场了。其对数似然函数为：

l(ϕ,μ0,μ1,Σ)=log∏i=1mp(x(i),y(i))=log∏i=1mp(x(i)|y(i))p(y(i))=∑i=1mlogp(x(i)|y(i))+∑i=1mlogp(y(i))=∑i=1mlog(p(x(i)|y(i)=0)1−y(i)+p(x(i)|y(i)=1)y(i))+∑i=1mlogp(y(i))=∑i=1m(1−y(i))logp(x(i)|y(i)=0)+∑i=1my(i)logp(x(i)|y(i)=1)+∑i=1mlogp(y(i))

　　注意此函数第一部分只和 μ0,Σ 有关，第二部分只和 μ1,Σ 有关，最后一部分只和 ϕ 有关。最大化该函数，首先求 ϕ ,先对其求偏导数：

∂l(ϕ,μ0,μ1,Σ)∂ϕ=∑mi=1logp(y(i))∂ϕ=∂∑mi=1logϕy(i)(1−ϕ)1−y(i))∂ϕ=∂∑mi=1y(i)logϕ+(1−y(i))log(1−ϕ)∂ϕ=∑i=1m(y(i)1ϕ−(1−y(i))11−ϕ)=∑i=1m(I(y(i)=1)1ϕ−I(y(i)=0)11−ϕ)

　　此处 I 为指示函数。令其为0，可求解出：

ϕ=I(y(i)=1)I(y(i)=0)+I(y(i)=1)=I(y(i)=1)m  

　　同样地，对 μ0 求偏导数：

∂l(ϕ,μ0,μ1,Σ)∂μ0=∂∑mi=1(1−y(i))logp(x(i)|y(i)=0)∂μ0=∂∑mi=1(1−y(i))(log1(2π)n|Σ|√−12(x(i)−μ0)TΣ−1(x(i)−μ0))∂μ0=∑i=1m(1−y(i))(−Σ−1(x(i)−μ0))=∑i=1m−I(y(i)=0)Σ−1(x(i)−μ0)  

　　令其为0，可求解得：

μ0=∑mi=1I(y(i)=0)x(i)I(y(i)=0)  

　　根据对称性可直接得出：

μ1=∑mi=1I(y(i)=1)x(i)I(y(i)=1)  

　　下面对 Σ 求偏导数，由于似然函数只有前面两部分与 Σ 有关，则将前两部分改写如下：

∑i=1m(1−y(i))logp(x(i)|y(i)=0)+∑i=1my(i)logp(x(i)|y(i)=1)=∑i=1m(1−y(i))(log1(2π)n|Σ|−−−−−−−√−12(x(i)−μ0)TΣ−1(x(i)−μ0))+∑i=1my(i)(log1(2π)n|Σ|−−−−−−−√−12(x(i)−μ1)TΣ−1(x(i)−μ1))=∑i=1mlog1(2π)n|Σ|−−−−−−−√−12∑i=1m(x(i)−μy(i))TΣ−1(x(i)−μy(i))=∑i=1m(−n2log(2π)−12log(|Σ|))−12∑i=1m(x(i)−μy(i))TΣ−1(x(i)−μy(i))

　　进而有：

∂l(ϕ,μ0,μ1,Σ))∂Σ=−12∑i=1m(1|Σ||Σ|Σ−1)−12∑i=1m(x(i)−μy(i))T(x(i)−μy(i))∂Σ−1∂Σ=−m2Σ−1−12∑i=1m(x(i)−μy(i))T(x(i)−μy(i))(−Σ−2))

　　这里推导用到了：

∂|Σ|∂Σ=|Σ|Σ−1

∂Σ−1∂Σ=−Σ−2  

　　令其为0，从而求得：

Σ=1m∑i=1m(x(i)−μy(i))T(x(i)−μy(i))  

　　上面的推导似乎很复杂，但其结果却是非常简洁。通过上述公式，所有的参数都已经估计出来，需要判断一个新样本x时，可分别使用贝叶斯求出p(y=0|x)和p(y=1|x)，取概率更大的那个类。

　　实际计算时，我们只需要比大小，那么贝叶斯公式中分母项可以不计算，由于2个高斯函数协方差矩阵相同，则高斯分布前面那相同部分也可以忽略。实际上，GDA算法也是一个线性分类器，根据上面推导可以知道，GDA的分界线(面)的方程为：

         (1−ϕ)exp((x−μ0)TΣ−1(x−μ0)=ϕexp((x−μ1)TΣ−1(x−μ1)

　　取对数展开后化解，可得：

  2xTΣ−1(μ1−μ0)=μT1Σ−1μ1−μT0Σ−1μ0+logϕ−log(1−ϕ)

　　若 A=2Σ−1(μ1−μ0)=(a1,a2,...,an)b=μT1Σ−1μ1−μT0Σ−1μ0+logϕ−log(1−ϕ) ，则

  a1x1+a2x2+...+anxn=b

　　这就是GDA算法的线性分界面。

 

GDA实现

---

　　这里也采用前面讲逻辑回归生成的数据来进行实验，直接load进来进行处理，详见逻辑回归。GDA训练代码如下： 

  View Code

 　　测试代码： 

  View Code

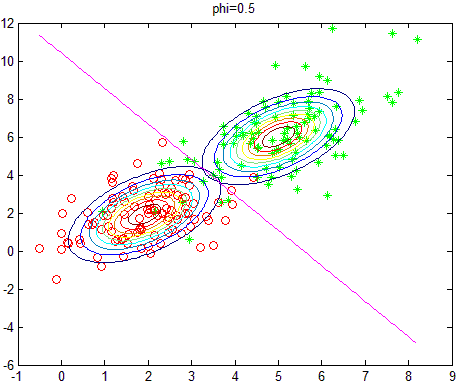
　　训练结果如下，训练样本中，正负样本均为100个，故 ϕ=0.5 ：

 

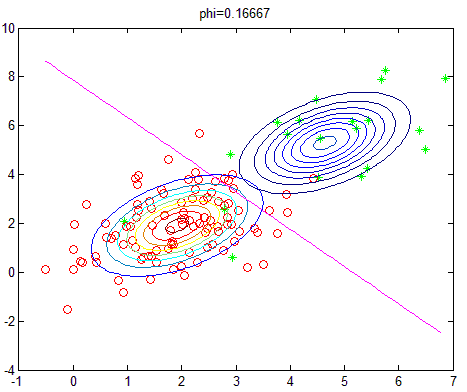
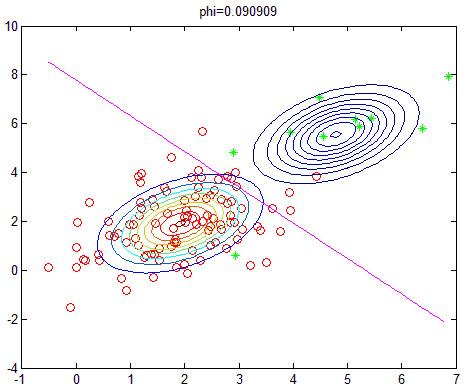
　　改变正负样本数量，即相当于改变先验概率，则实验结果如下(相应的 ϕ 的值显示在图像标题)：

       

 

算法分析

---

　　1.与逻辑回归的关系

　　　　根据上面的结果以及贝叶斯公式，可有

  p(y=1|x)=p(x|y=1)p(y=1)p(x)=N(μ1,Σ)ϕN(μ0,Σ)(1−ϕ)+N(μ1,Σ)ϕ=1/(1+N(μ0,Σ))N(μ1,Σ)1−ϕϕ)

　　　　而

N(μ0,Σ)N(μ1,Σ)=exp{(x−μ0)TΣ−1(x−μ0)−(x−μ1)TΣ−1(x−μ1)}=exp{2(μ1−μ0)TΣ−1x+(μT0Σμ0−μT1Σμ1)}

　　　　那么,令

2Σ−1(μ1−μ0)=(θ1,θ2,...,θn)Tθ0=μT0Σμ0−μT1Σμ1+log1−ϕϕ

　　　　则

p(y=1|x)=11+exp(θ0+θ1x1+θ2x2+...+θnxn)

　　　　这不就是逻辑回归的形式么？

　　　　在推导逻辑回归的时候，我们并没有假设类内样本是服从高斯分布的，因而GDA只是逻辑回归的一个特例，其建立在更强的假设条。故两者效果比较：

　　　　a.逻辑回归是基于弱假设推导的，则其效果更稳定，适用范围更广

　　　　b.数据服从高斯分布时，GDA效果更好

　　　　c.当训练样本数很大时，根据中心极限定理，数据将无限逼近于高斯分布，则此时GDA的表现效果会非常好

 

　　2.为何要假设两类内部高斯分布的协方差矩阵相同？

　　　　从直观上讲，假设两个类的高斯分布协方差矩阵不同，会更加合理（在混合高斯模型中就是如此假设的），而且可推导出类似上面简洁的结果。

　　　　假定两个类有相同协方差矩阵，分析具有以下几点影响：

　　　　A．当样本不充分时，使用不同协方差矩阵会导致算法稳定性不够；过少的样本甚至导致协方差矩阵不可逆，那么GDA算法就没法进行

　　　　B．使用不同协方差矩阵，最终GDA的分界面不是线性的，同样也推导不出GDA的逻辑回归形式

 

　　3.使用GDA时对训练样本有何要求？

　　　　首先，正负样本数的比例需要符合其先验概率。若是预先明确知道两类的先验概率，那么可使用此概率来代替GDA计算的先验概率；若是完全不知道，则可以公平地认为先验概率为　　50%。

　　　　其次，样本数必须不小于样本特征维数，否则会导致协方差矩阵不可逆，按照前面分析应该是多多益善。