LeetCode126—Word Ladder II

LeetCode126—Word Ladder II

据说是全LeetCode通过率最低的题，确实非常难，但从算法层面讲还不至于到想不到写不了的地步，只是说很多细节需要注意，我在提交过程中遇到的两个主要问题是：超时（Time Limit Exceed）和超出内存限制（Memory Limit Exceed）。

1.原题

Given two words (beginWord and endWord), and a dictionary’s word list, find all shortest transformation sequence(s) from beginWord to endWord, such that:

Only one letter can be changed at a time
Each intermediate word must exist in the word list
For example,

Given:
beginWord = “hit”
endWord = “cog”
wordList = [“hot”,”dot”,”dog”,”lot”,”log”]
Return
[
[“hit”,”hot”,”dot”,”dog”,”cog”],
[“hit”,”hot”,”lot”,”log”,”cog”]
]

---

2.分析

与LeetCode127—Word Ladder的意思一样，隐式的图论的题目，这题相对更难，原因是需要求出所有的路径，而前者只需要求出路径长度即可（事实上这可以从数据结构设计上忽略不少细节，在这题中就体现的淋漓尽致）。这样我们就很快有了一个比较清晰的思路，首先：

1. 首先，为了得出所有路径（可能有多条，并且可能多条通过同一个节点），其中一个节点可能被访问多次，我们想到了dfs，因为在递归的返回的过程中包含了回溯。
2. 如果对beginWord、endWord以及wordList中的所有单词建立一个图的话，当数据量上去的时候，这个图将非常之大（主要体现在边的规模有可能非常大）
3. 考虑到在Word Ladder中求路径的方法，我们可以建立一个部分信息的图——即仅仅保留BFS遍历过程中某些节点的前驱节点。这样我们就可以得到一个“有向图”（这里并不是真正的有向图，只是形式上很像），这个“有向图”可以以邻接表的方式来体现，就好像迪杰斯特拉一样知道每个节点的前驱节点最终递归得到整条路径。

总结一下，这个题的思路就是：
BFS -> 求出每个节点的前驱节点
DFS -> 从后往前搜索出路径

---

3.细节

这里有两个细节，一个是时间优化，一个是空间优化。

时间优化

首先所有的参数都用引用肯定是必要的，单个变量就罢了，对于这种有容器的还是用引用比较高效。

BFS在遍历的时候按层进行遍历的，由于我们这里要找出所有有用的前驱节点，所以在BFS的时候要做一些手脚：
那就是每一层结束之后，再对visit属性进行调整，但因此，这里就会出现问题，看下图：

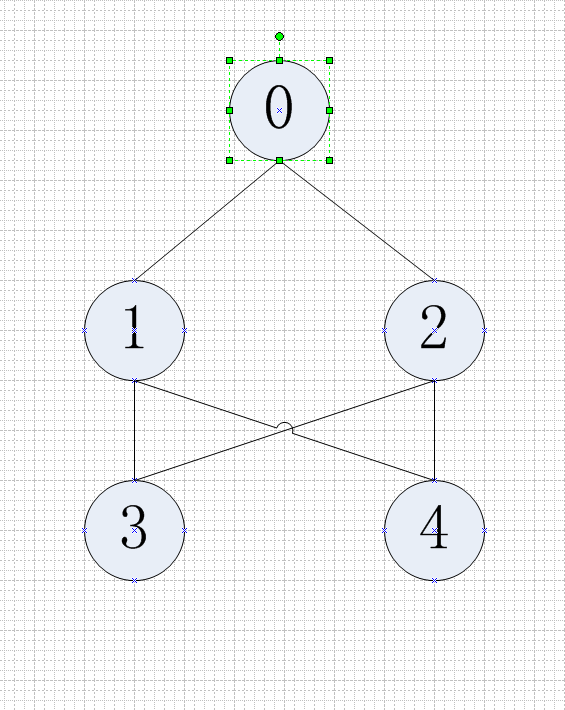
BFS访问完节点0后，此时节点1和节点2入队，然后节点1出队，节点3节点4入队，这里，由于要得出所有可能路径，对于节点3和节点4来说，其前驱节点要把节点1和节点2都要记录。传统的BFS，当节点1出队后，伴随的会让节点3和节点4入队且标记为visit，这样节点2出队的时候就不会再把节点3和节点4访问一次了。。。当然，这样显然不行的，所以我们要再节点1和节点2这一层访问完后，再对节点3节点4标记，让其将节点2作为其前驱节点记录。不过这个时候问题又来了：那你不及时标记节点3和节点4，那在访问节点2的时候不是又会把节点3和节点4入队？这个问题，就要有一个小技巧了，留在代码中解释。

空间优化

这一步不做的话，OJ会直接报出Memory Limit Exceed 的错误。

也是想了很久，设想一种状况：刚才提到，我们需要一个“邻接表形式的有向图”，不管图的节点内容是什么，索引肯定是要整型表示吧，于是我们构建一个map，来作为string->int的映射，假设我们前驱节点也是以索引来表示的，在最终DFS时，还需要一个int->string的映射。

这里花了很长时间，一直Memory Limit Exceed

于是我想，能不能以一种方式不需要映射来映射去的呢？比如我想知道“hot”这个单词的前驱节点，能不能让索引就是“hot”，而其前驱节点就是“hit”呢？
我的办法就是用这样一种结构来保存前驱节点map>

---

代码

class Solution {
private:
    void isConnected(vector<string>&connect, unordered_set<string>& wordList, const string ¤t, const string & end, unordered_set<string>&visit)
    {
        connect.clear();
        string cur = current;
        for (int i = 0; i < cur.size(); i++)
        {
            char t = cur[i];
            for (char c = 'a'; c < 'z'; c++)
            {
                if (c == t)
                {
                    continue;
                }
                cur[i] = c;
                if ((cur == end || wordList.find(cur) != wordList.end()) && (visit.find(cur) == visit.end()))
                {
                    connect.push_back(cur);
                }

            }
            cur[i] = t;
        }
    }// isConnect求当前节点相连多所有节点

    //BFS
    void bfs(map<string,vector<string>>&preNode, unordered_set<string>&wordList, const string &beginWord, const string& endWord)
    {
        queue<string>q;
        unordered_set<string>visit;//是否访问
        visit.insert(beginWord);
        vector<string>connect;
        q.push(beginWord);
        while (!q.empty())
        {
            int len = q.size();
            vector<string> tmpVisit;
            while (len--)
            {
                string current = q.front();
                q.pop();
                isConnected(connect, wordList, current, endWord, visit);
                for (int i = 0; i < connect.size(); i++)
                {
                    if (visit.find(connect[i]) == visit.end())//未被访问
                    {
                        if (preNode[connect[i]].empty())//这个判断语句为了防止图中所说情况
                        {
                            tmpVisit.push_back(connect[i]);
                            q.push(connect[i]);
                        }

                        preNode[connect[i]].push_back(current);
                    }
                }
            }//每一层
            for (int j = 0; j < tmpVisit.size(); j++)//每一层结束记录访问节点
            {
                visit.insert(tmpVisit[j]);
            }
            if (visit.find(endWord) != visit.end())
                return;
        }
    }

    //DFS
    void dfs(const string &beginWord, const string &t, vector<string>tmp, map<string,vector<string>>&preNode, vector<vector<string>>&result)
    {
        if (t == beginWord)
        {
            tmp.push_back(beginWord);
            vector<string>tmpres(tmp.rbegin(), tmp.rend());
            result.push_back(tmpres);
            return;
        }
        tmp.push_back(t);
        for (int i = 0; i < preNode[t].size(); i++)
            dfs(beginWord, preNode[t][i], tmp, preNode, result);
    }
public:
    vector<vector<string>> findLadders(string beginWord, string endWord, unordered_set<string> &wordList) {
        wordList.insert(endWord);
        map<string, vector<string>>preNode;//记录前驱节点



        bfs(preNode, wordList, beginWord, endWord);
        //bfs -> 每个节点的前驱节点
        vector<vector<string>>result;
        vector<string>tmp;
        dfs(beginWord, endWord, tmp, preNode, result);
        //dfs -> 从后往前搜索出路径
        return result;
    }
};