线性代数(3)
目录
- A x = b Ax=b Ax=b无解时的求解
- 空间投影
- 最小二乘上的应用
- 正交矩阵
- Gram-Schmidt正交化
- A = Q R 分 解 A=QR分解 A=QR分解
A x = b Ax=b Ax=b无解时的求解
从线性代数(1)列空间的讨论可知,如果 b b b不在 A A A的列空间 C ( A ) C(A) C(A)内,那么 A x = b Ax=b Ax=b无解
在实际应用中这种无解的情况很多:
1)因为观察/测量的数据总会有误差,无法保证每个 b i b_i bi都是精确的;
2)未知数少,而限制条件多
先说结论:将 A x = b Ax=b Ax=b转为求
A T A x ^ = A T b (1) A^TA\hat{x}=A^Tb \tag{1} ATAx^=ATb(1)
- 式(1)的解是 A x = b Ax=b Ax=b的最优解
- 如果 C ( A ) C(A) C(A)线性无关,那么 A T A A^TA ATA必然可逆
空间投影
先探讨一维向量空间的情况
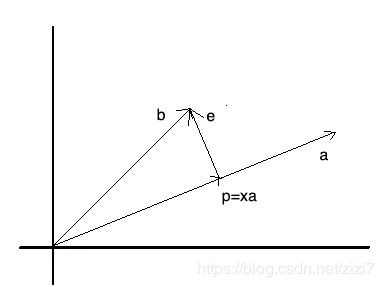
如图1, p ⃗ \vec{p} p是 b ⃗ \vec{b} b在 a ⃗ \vec{a} a上的投影,有
p ⃗ = x a ⃗ e ⃗ = b ⃗ − p ⃗ (2) \vec{p}=x\vec{a}\\\vec{e}=\vec{b}-\vec{p} \tag{2} p=xae=b−p(2)
显然, e ⃗ \vec{e} e垂直于 a ⃗ \vec{a} a,根据正交向量点积为0的定理,有
a T ( b − x a ) = 0 ⇒ x = a T b a T a ⇒ p = x a = a a T b a T a ⇒ P = a a T a T a (3) a^T(b-xa)=0\\\Rightarrow x=\frac{a^Tb}{a^Ta}\\\ \ \ \ \ \ \ \ \ \ \ \Rightarrow p=xa=a\frac{a^Tb}{a^Ta}\\\Rightarrow P=\frac{aa^T}{a^Ta} \tag{3} aT(b−xa)=0⇒x=aTaaTb ⇒p=xa=aaTaaTb⇒P=aTaaaT(3)
式(3)中 P P P为投影矩阵,将 b ⃗ \vec{b} b投影到 a ⃗ \vec{a} a上
投影矩阵3条性质:
1.秩为1(如式3,投影矩阵为列向量与行向量乘积,满足秩1矩阵的性质)
2.转置不变: P T = P P^T=P PT=P,说明投影矩阵是对称矩阵
3.平方不变: P 2 = P P^2=P P2=P(投影2次和投影1次结果一样)
现在在二维空间中讨论 A x = b Ax=b Ax=b解的问题
假设 A A A的列空间基为 a 1 a_1 a1、 a 2 a_2 a2,那么当 b b b不在 a 1 a_1 a1和 a 2 a_2 a2确定的平面内时, A x = b Ax=b Ax=b无解
现在假设 c c c是 b b b在 a 1 a_1 a1和 a 2 a_2 a2确定的平面上的投影,即
c = x ^ 1 a 1 + x ^ 2 a 2 (4) c=\hat{x}_1a_1+\hat{x}_2a_2 \tag{4} c=x^1a1+x^2a2(4)
那么 A x ^ = c A\hat{x}=c Ax^=c肯定有解,而且是 A x = b Ax=b Ax=b误差最小的解
令 e e e为从 b b b到 c c c的投影“垂线”,那么有
e = b − A x ^ (5) e=b-A\hat{x} \tag{5} e=b−Ax^(5)
并且
a 1 T ( b − A x ^ ) = 0 a 2 T ( b − A x ^ ) = 0 (6) a_1^T(b-A\hat{x})=0\\a_2^T(b-A\hat{x})=0 \tag{6} a1T(b−Ax^)=0a2T(b−Ax^)=0(6)
将式(6)表示为矩阵形式
A T ( b − A x ^ ) = 0 (7) A^T(b-A\hat{x})=0 \tag{7} AT(b−Ax^)=0(7)
从而
x ^ = ( A T A ) − 1 A T b (8) \hat{x}=(A^TA)^{-1}A^Tb \tag{8} x^=(ATA)−1ATb(8)
式(8)就是 A x = b Ax=b Ax=b的最优解
最小二乘上的应用
假设有3组二维数据 [ 1 1 ] T [1\ 1]^T [1 1]T、 [ 2 2 ] T [2\ 2]^T [2 2]T、 [ 3 2 ] T [3\ 2]^T [3 2]T,需要拟合一条误差最小的直线
令直线为 y = x 1 + x 2 t y=x_1+x_2t y=x1+x2t,上述问题可以表示为式(9)的矩阵形式
[ 1 1 1 2 1 3 ] [ x 1 x 2 ] = [ 1 2 2 ] (9) \left[\begin{matrix}1&1\\1&2\\1&3\end{matrix}\right]\left[\begin{matrix}x_1\\x_2\end{matrix}\right]=\left[\begin{matrix}1\\2\\2\end{matrix}\right] \tag{9} ⎣⎡111123⎦⎤[x1x2]=⎣⎡122⎦⎤(9)
显然上式无解,应用式(8),可求得最优解: x ^ = [ 2 3 1 2 ] T \hat{x}=[\frac{2}{3}\ \frac{1}{2}]^T x^=[32 21]T
即拟合的直线方程为 y = 2 3 + 1 2 t y=\frac{2}{3}+\frac{1}{2}t y=32+21t
现在用传统的目标函数的方式求解:
m i n [ ( x 1 + x 2 − 1 ) 2 + ( x 1 + 2 x 2 − 2 ) 2 + ( x 1 + 3 x 2 − 2 ) 2 ] (10) min[(x_1+x_2-1)^2+(x_1+2x_2-2)^2+(x_1+3x_2-2)^2] \tag{10} min[(x1+x2−1)2+(x1+2x2−2)2+(x1+3x2−2)2](10)
式(10)分别对 x 1 x_1 x1和 x 2 x_2 x2求偏导,有
3 x 1 + 6 x 2 = 5 6 x 1 + 14 x 2 = 11 (11) 3x_1+6x_2=5\\6x_1+14x_2=11 \tag{11} 3x1+6x2=56x1+14x2=11(11)
求解上述方程组,得 x 1 = 2 3 x_1=\frac{2}{3} x1=32, x 2 = 1 2 x_2=\frac{1}{2} x2=21,与式(8)得到的结果一致
正交矩阵
标准正交向量: q i T q j = { 0 i ≠ j 1 i = j q_i^Tq_j=\begin{cases}0&i\neq j\\1&i=j\end{cases} qiTqj={01i=ji=j
正交矩阵: Q = [ q 1 q 2 . . . q n ] Q=\left[\begin{matrix}q_1&q_2&...&q_n\end{matrix}\right] Q=[q1q2...qn],其中 q i q_i qi互相为标准正交向量,并且 Q Q Q为方阵
需要注意正交矩阵必须为方阵,这个是历史原因,其实并没道理
根据正交矩阵的定义,一定有
Q T Q = I Q T = Q − 1 (12) Q^TQ=I\\Q^T=Q^{-1} \tag{12} QTQ=IQT=Q−1(12)
Gram-Schmidt正交化
给定一个线性无关向量组 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,可以通过施密特正交法将其转换为相互正交的向量组 b 1 , b 2 , . . . , b n b_1,b_2,...,b_n b1,b2,...,bn
b 1 = a 1 b 2 = a 2 − < a 2 , b 1 > < b 1 , b 1 > b 1 b 3 = a 3 − < a 3 , b 1 > < b 1 , b 1 > b 1 − < a 3 , b 2 > < b 2 , b 2 > b 2 . . . b n = a n − < a n , b 1 > < b 1 , b 1 > b 1 − < a n , b 2 > < b 2 , b 2 > b 2 − . . . − < a n , b n − 1 > < b n − 1 , b n − 1 > b n − 1 (13) \begin{aligned}b_1 &=a_1\\b_2&=a_2-\frac{
式(13)的 b i ∣ ∣ b i ∣ ∣ \frac{b_i}{||b_i||} ∣∣bi∣∣bi便得到标准正交向量
式(13)的 < a n , b n − 1 > < b n − 1 , b n − 1 > = b n − 1 T a n b n − 1 T b n − 1 (14) \frac{
回忆空间投影里的式(2)和(3),可以发现(13)的形式与其一致
事实上式(13)可以解释为: b 2 b_2 b2是 a 2 a_2 a2投影到 a 1 a_1 a1的那个 e e e(图1)
A = Q R 分 解 A=QR分解 A=QR分解
对任意 A ∈ R m × n ( m ≥ n ) A\in \mathbb{R}^{m\times n}(m\geq n) A∈Rm×n(m≥n),总有 A = Q R (15) A=QR \tag{15} A=QR(15)
其中 Q ∈ R m × n Q\in \mathbb{R}^{m\times n} Q∈Rm×n,其列空间是 A A A列空间的标准正交向量
其中 R ∈ R n × n R\in \mathbb{R}^{n\times n} R∈Rn×n是上三角矩阵 [ r 1 r 2 0 r 3 ] \left[\begin{matrix}r_1&r_2\\0&r_3\end{matrix}\right] [r10r2r3]