c++强连通算法

一、强连通图

强连通图就是在一个有向图中有许多的点，有一些有向边连接这些点，这些点之中任意两个都能相互到达，这就是强连通图

二、强连通分量

一个有向图中，选出某些点组成一个团体，这个团体中的任意两点都可互相到达。那么：选出来的这些点+这些点之间原有的边=叫做 连通分量

三、什么时候使用强连通

在有向图的时候才可以用，无向图用并查集就可以解决了

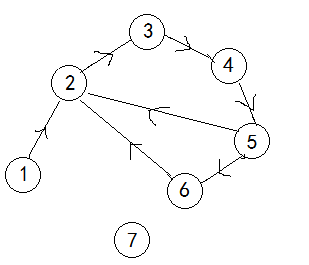
那么我们看一下例题(caioj.cn1147)

题目描述
【题目描述】

   给出一个有向图有n个点和m条有向边，输出连通分量的数量。

【输入格式】
   第一行n和m（1<=n<=20000,1<=m<=20 0000），表示有向图总共n个点，点的编号由1~n。m表示m条有向边。
下来m行，每行两个整数x和y，表示一条有向边从点x出发到点y。
【输出格式】
   一行一个整数，表示连通分量的个数。
【样例1输入】
7 7
1 2
2 3
3 4
4 5
5 6
6 2
5 2
【样例1输出】

3

下面是样例的图

下面就用一个大肚子人国的故事来描述这一个算法（样例）

据说，郑和七下西洋的时候发现了一个大肚子人国，国家里面每一个人都有一个大肚子

每个人的头上有一个编号：      dfn，表示这一个人的职位的大小（1比2的职位要大）

每个人的肚子上也有一个编号：low，表示这一个人所在小团体里面老大的职位（有福同享嘛，这样才能在其它的小团体面前耀武扬威）

每个人后背还有一个编号:        belong，表示这个人所在的小团体的编号（不分大小）

一开始，这个国家里面每一个人都不知道另外一个人存在

郑和找到了第一个人说：“我封你为国王，你的编号为1，下面，你就沿着这些（条)路找你的大臣吧"

一号编号的人找到了下一个人，封他为大臣，编号为2

二号编号的人。。。。。。

一直找到了编号为5的人

5也沿着一条路找到了2,5对2说：“你的官职可真大啊，你做我的老大吧，于是5把肚子上的编号改为2，他认为自己的权利大了，他很开心”

5后来又命令6去找，6去找2改完肚子的编号，报告回5，我比较自己和6的肚子编号发现一样，就什么都不管

5找完后汇报给4，4说“你老大的官职比我的大（肚子编号比我的小），我们都认这个老大吧”

。。。。。。

这样一直找到了2,2汇报给1,2发现1老大的官职还是比自己的官职大，2很不服气，就自己去当这个小团体的老大了，于是两个团体就诞生了

后来，郑和找到了7，给了他编号，因为7于是隔绝，“乃不知有汉，无论魏晋”，于是他自己做了老大，第三个团体就诞生了

三个团体:(1)，（2,3,4,5,6），（7)

扯不下去了，讲代码吧：

#include
using namespace std;
struct node
{
    int x,y,next;
}a[5100000];int len,last[21000];
inline void ins(int x,int y)//建立有向边 
{
    len++;a[len].x=x;a[len].y=y;
    a[len].next=last[x];last[x]=len;
}
int cnt,belong[21000];//cnt表示连通分量的个数,belong表示这一个人的小团体编号 
int id,low[21000],dfn[21000];//id记录当前搜索点的dfs的顺序号，low表示肚子，dfn表示额头 
int tp,sta[21000];bool v[21000];//sta为栈,tp为栈顶标签，v[i]表示点是否在栈里面
void dfs(int x)
{
    dfn[x]=low[x]=++id;//一开始额头和肚子都是一样的编号
    sta[++tp]=x;v[x]=true;//一开始自己团体的老大
    for(int k=last[x];k;k=a[k].next)//访问亲朋好友 
    {
        int y=a[k].y;
        if(dfn[y]==0)//如果y没有被访问过 
        {
            dfs(y);
            low[x]=min(low[x],low[y]);//看看谁老大的编号更大 
        }
        else//如果y已经被访问过，而且还没有出栈
        //说明在这之前有y->x的路线，现在x到y有边，所以x和y之间构成回路
        {
            if(v[y]==true) low[x]=min(low[x],dfn[y]);//如果是在栈里面（不属于别的小团体），就看看是否能让他当你的老大 
        }
    }
    if(low[x]==dfn[x])//如果是小团体老大的话 
    {
        int i;cnt++;//增加一个小团体 
        do
        {
            i=sta[tp--]; //出栈 
            v[i]=false;//标记i已经出栈 
            belong[i]=cnt;//标记i所属的连通分量的离散标号 
        }while(i!=x);
    }
}
int main()
{
    int i,n,m;scanf("%d%d",&n,&m);//输入以及初始化 
    for(i=1;i<=m;i++)
    {
        int x,y;scanf("%d%d",&x,&y);
        ins(x,y);
    }
    memset(v,false,sizeof(v));
    for(i=1;i<=n;i++)//全部找一次（一次找不完） 
    {
        if(dfn[i]==0)//如果没有找过 
            dfs(i);
    }
    printf("%d\n",cnt);
    return 0;
}

这个代码看起来很和谐

好了，这就是强连通代码

下面来一个例题（USACO5.3校园网，第二问是caioj.cn1148)

题目描述
【题意】
给出N(2<=N<=100)个点以及一些有向边，你可以往一些点分发软件，然后这些软件将自动从这些点分发到可以到达的其他点。现有两个问题：1.若想让所有点都得到软件，你一开始最少需要分发软件的点数；2.若想从任意一个点分发软件，就可以使所有点得到软件，最少需要添加多少条有向边。

【输入格式】
输入文件的第一行包括一个整数 N：点的数目（2 <= N <= 100）。点的编号为1到N。
接下来 N 行中每行有若干个整数，最后以0为结尾。第i+1行第j个数表示点i通向点j(i,j之间有一条有向边)。

【输出格式】
第一行为问题1的解，第二行为问题2的解，都是一个正整数。

【输入样例】
5
2 4 3 0
4 5 0
0
0
1 0
【输出样例】
1

2

这一道题就用刚才的方法来缩一次点，找小团体的编号（belong）

第一问：缩点后，找入度为0的点（不为0可以通过别的点传过来）

第二问：缩点后，入度为0的点和出度为0的点的最大值，可以看成一个环（至少每一个点都要有一条边进入，一条边出去）

代码：

#include
using namespace std;
struct node
{
    int x,y,next;
}a[11000];int len,last[110];
int tp,sta[110];bool v[110];
int id,cnt,belong[110],dfn[110],low[110];
int into[110],out[110];
inline void ins(int x,int y)
{
    len++;
    a[len].x=x;a[len].y=y;
    a[len].next=last[x];last[x]=len;
}
void dfs(int x)
{
    tp++;sta[tp]=x;
    dfn[x]=low[x]=++id;v[x]=true;
    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(dfn[y]==0)
        {
            dfs(y);
            low[x]=min(low[x],low[y]);
        }
        else
        {
            if(v[y]==true) low[x]=min(low[x],low[y]);
        }
    }
    if(low[x]==dfn[x])
    {
        int i;cnt++;
        do
        {
            i=sta[tp--];
            v[i]=false;
            belong[i]=cnt;
        }while(i!=x);
    }
}
int main()
{
    int n,m;scanf("%d",&n);
    len=0;memset(last,0,sizeof(last));
    for(int x=1;x<=n;x++)
    {
        int y;
        while(scanf("%d",&y)!=EOF)
        {
            if(y==0) break;
            ins(x,y);
        }
    }
    memset(v,false,sizeof(v));
    for(int i=1;i<=n;i++)
    {
        if(dfn[i]==0)
            dfs(i);
    }//以上和模版的代码99%一样 
    if(cnt==1)//如果只有一个小团体（特判） 
    {
        printf("1\n0\n");
        return 0;
    }
    for(int i=1;i<=len;i++)//找入度为0的点和出度为0的点 
    {
        int tx=belong[a[i].x],ty=belong[a[i].y];
        if(tx!=ty)
        {
            into[ty]++;out[tx]++;
        }
    }
    int ans1,ans2;ans1=ans2=0;
    for(int i=1;i<=cnt;i++)
    {
        if(into[i]==0) ans1++;
        if(out[i]==0) ans2++;
    }
    printf("%d\n%d\n",ans1,max(ans1,ans2));
    return 0;
}