关于叉积
学过计算几何以后,我发现几乎每一道题都用到了叉积这个东西
叉积是什么呢
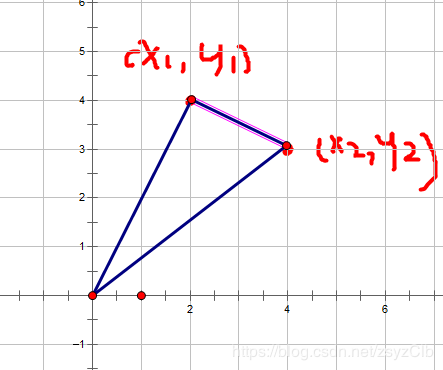
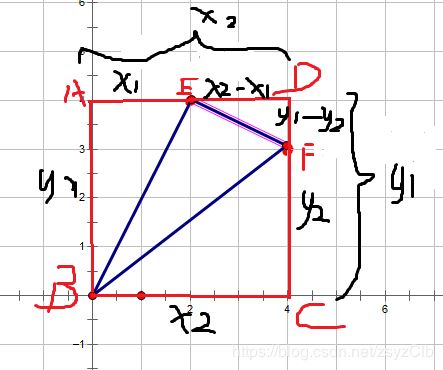
在这个图中(以原点为中心)叉积就是x1*y2-x2*y1
( 记得话就记1221,x前y后)
但是这并不是完全正确
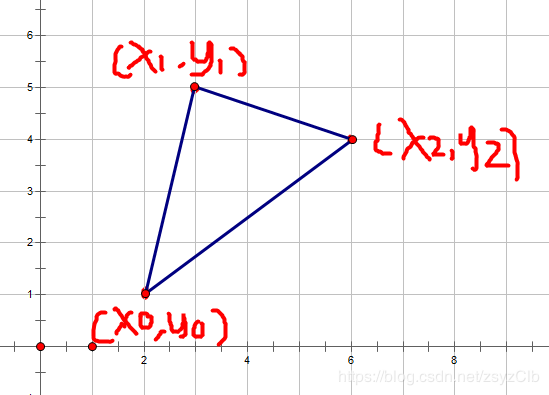
比如说这个图
在这个图中,点1和点2是以点0为中心,不是原点
因此我们可以把点0当成原点
则
x1 = p1.x-p0.x;
y1 = p1.y-p0.y;
x2 = p2.x-p0.x;
y2 = p2.y-p0.y;
(p1表示点1,p2表示点2,p0表示点0 )
在此之后,我们又可以用原来x1*y2-x2*y1的公式来求叉积了
所以叉积的代码是
int multi ( node p1 , node p2 , node p0 ) {
int x1 , y1 , x2 , y2 ;
x1 = p1.x-p0.x , y1 = p1.y-p0.y ;
x2 = p2.x-p0.x , y2 = p2.y-p0.y ;
return x1*y2 - x2*y1 ;
}注意一下double和int的类型
第二个问题就是叉积怎么用
当我一开始学习计算几何根本就不懂叉积的意思是什么
我听老师说如果
叉积>0 , 则以点0为中心点1逆时针转向点2
叉积=0,则三点共线
叉积<0 , 则以点0为中心点1顺时针转向点2
终于理解了意思,但为什么是这样呢,我用各种方法都没有知道原因
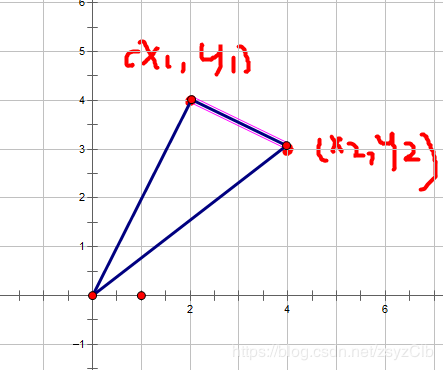
直到我做了一道题,就是求三角形的面积(边不一定与坐标轴平行)
然后老师用了叉积除以2就可以得到面积
起初我不信,然后就试了很多种情况,都证明这个结论是对的
我研究了好一会儿,才理解了原理
把刚才的那个图片拿出来
我们给ta做一个辅助线
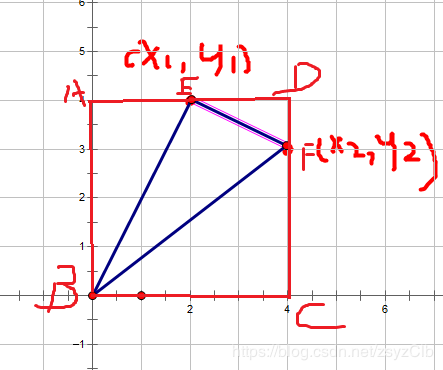
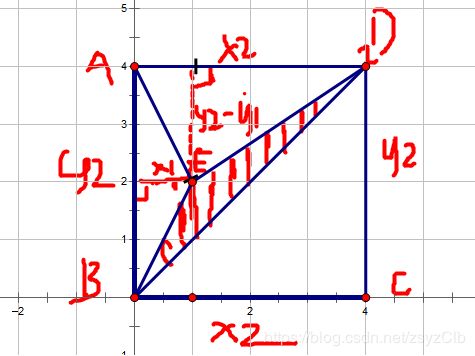
变成这样
据图得知
AE = x1 , AB = CD = y1 , BC = AD = x2 , CF= y2
DE = BC-AE = x2-x1 , DF = DC-FC = y1-y2
呵呵,图片似乎有点丑
S正方形ABCD = AB * BC = x2*y1
S▲ABE = AE * AB / 2 = x1*y1/2
S▲EDF = ED*DF/2 = (x2-x1)*(y1-y2)/2 = (x2*y1-x2*y2-x1*y1+x1*y2 ) / 2
S▲BCF = BC * CF / 2 = x2*y2/2
所以
S▲BEF = S正方形ABCD - S▲ABE - S▲EDF - S▲BCF
= x2*y1- ( x1*y1 + x2*y1-x2*y2-x1*y1+x1*y2 + x2*y2 ) / 2
= x2*y1 - ( x2*y1 + x1*y2 ) / 2
= - ( x1*y2 - x2*y1 ) / 2
记得前面有个负号
补充一下
对于钝角三角形,就连接连接钝角顶点和矩形的一个顶点,还是可以证明的
这个面积不仅解释了叉积求面积的问题,也解释了前面的问题
叉积>0 , 则以点0为中心点1逆时针转向点2
叉积<0 , 则以点0为中心点1顺时针转向点2
通过求面积,这两个理论也被很好的解释了
但还有一个,就是三点共线的问题
为什么三点共线的时候叉积就是0呢?
这个要分两种情况讨论
情况一 :点0不在中间
我们可以考虑将点0假设成原点
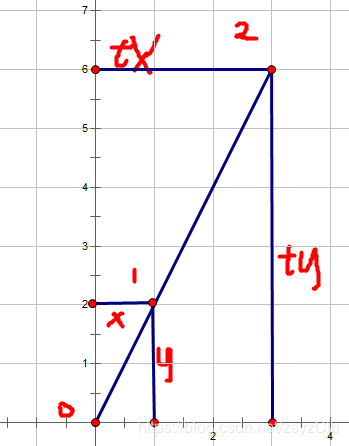
然后过点1和点2向x轴,y轴分别作垂线
我们根据三角形全等和相似的结论可以求出
x2 = tx1 , y2 = ty1
叉积 = x1*y2-x2*y1 = x*ty - tx*y = txy-txy = 0
反过来亦是如此
情况2 :点0在中间
我们可以考虑先将点0变成原点
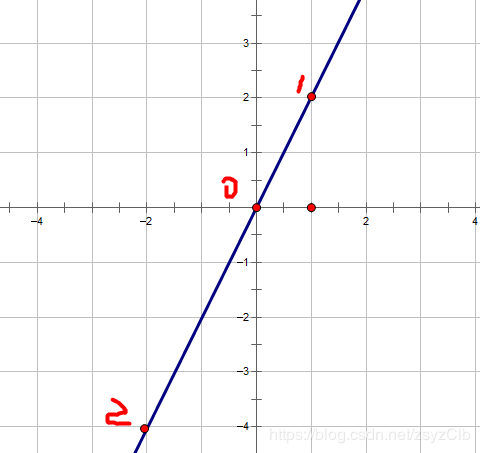
那么我们可以考虑给点2做一个原点对称点点3
点3就是 ( -x2 , -y2 ) , 也可以说点2是放过来的点3
根据情况2得出的结论,点3也是tx1和ty1
也就是说 -x2 = tx1 , -y2 = ty1
叉积 = x1 * y2 - x2 * y1
= - x1*(-y2) + ( -x2) * y1
= - x1 * ty1 + tx1 * y1
= - t * x1 * y1 + t * x1 * y1
= 0
写了好久终于写完了!