Gradient Decent

梯度下降及其公式推导

最近在看Coursera上吴恩达的ml课程，在应用机器学习算法时，我们通常采用梯度下降法来对采用的算法进行训练。别人问到我梯度下降的问题时感觉自己还是有些不清晰，为此在这里做一个回顾复习巩固提升

梯度下降（Gradient Decent)的含义

在机器学习过程中，为最小损失函数（Cost Function)，我们通常使用梯度下降算法来一步一步迭代求解，以得到最小化的损失函数和参数模型。同时，在机器学习中，基于基本的梯度下降算法，还衍生出了随机梯度下降法和批量梯度下降法。

梯度下降中的相关概念

1. 假设函数（Hypothesis function）：在监督学习中，为拟合样本，通常使用一个假定的函数模型，记为 fθ(x) f θ ( x ) 。通常有：
   fθ(x)=θ0+θ1x1+θ2x2+…+θnxn f θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + … + θ n x n
2. 损失函数（Cost function）：在监督学习过程中，为函数评判拟合程度的大小，通常使用拟合函数来度量拟合程度的好坏。若损失函数越小则表示所选择的模型越优，得到的假设函数越靠近于真实情况。均方误差是是最常用的性能度量，因此我们可以构造损失函数：
   J(θ)=12m∑i=1m(fθ(xi)−yi)2 J ( θ ) = 1 2 m ∑ i = 1 m ( f θ ( x i ) − y i ) 2
3. 学习率/步长（Learning rate）：步长决定了在梯度下降过程中每次迭代时，沿梯度下降最快的方向前进的长度，通常记为 α α 。
4. 梯度（Gradient）：简单来讲，梯度就是某一函数在该点处方向倒数沿着该方向取得的最大值，即可理解为切线的方向。比如说，对于一个二维平面，则有
   ∇f=∂f∂xi⃗ +∂f∂yj⃗  ∇ f = ∂ f ∂ x i → + ∂ f ∂ y j →
   类似的有，对于一个三维空间，有
   ∇f=∂f∂xi⃗ +∂f∂yj⃗ +∂f∂zk⃗  ∇ f = ∂ f ∂ x i → + ∂ f ∂ y j → + ∂ f ∂ z k →

梯度下降模型直观理解

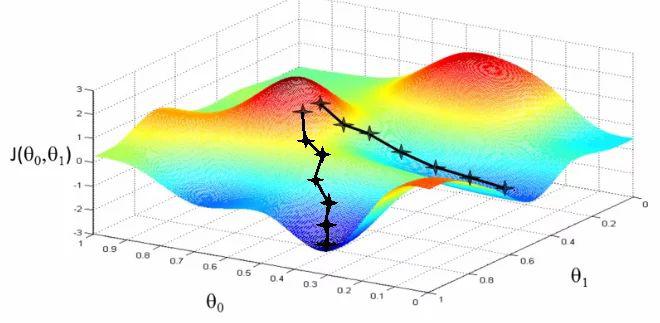
梯度下降的过程可以类比于一个下山的过程。假如此时你在山坡上的某一个位置，此时因为某些原因你不能看清周围的路，也就不知道下山的准确道路，此时如果你想下山，则应该寻找到一个沿梯度下降方向 ∇J(θ) ∇ J ( θ ) 的方向即朝往下最陡的方向走一步 α α ，经过多次迭代后，人总会走到一个最低点，虽然不一定是全局最优点但也应该是一个局部最优点，即一个局部最低的低谷。如图所示，易得，如果你的步长 α α 很短，则你会走很久才会走到这个局部最低点，而如果步长 α α 很大，则很难到达最低点，容易偏离原来的轨道甚至使得损失函数越来越大。

梯度下降算法的公式与解释

以下是梯度下降的公式：

θ　=　θ0−α∇f(θ0) θ 　 = 　 θ 0 − α ∇ f ( θ 0 )

其中 θ0 θ 0 是自变量，即你此时所在的坐标， α α 是学习率也就是每一步所走的长度， θ θ 是运动过后所在的位置坐标。
以下是对这个公式及 α α 的数学推导：
`首先对原函数进行一节泰勒展开式：

J(θ0)≈J(θ)+(θ0−θ)∇J(θ) J ( θ 0 ) ≈ J ( θ ) + ( θ 0 − θ ) ∇ J ( θ )

变形为

J(θ0)−J(θ)≈(θ0−θ)∇J(θ) J ( θ 0 ) − J ( θ ) ≈ ( θ 0 − θ ) ∇ J ( θ )

此时设 θ0−θ=ηv⃗  θ 0 − θ = η v → , v⃗  v → 是一个沿 (θ0−θ,0) ( θ 0 − θ , 0 ) 方向的一个单位向量，而 η η 是一个常量。
所以上式变化为

J(θ0)−J(θ)≈ηv⃗ ∇J(θ) J ( θ 0 ) − J ( θ ) ≈ η v → ∇ J ( θ )

若要使得算法梯度下降，则必有

J(θ0)−J(θ)<0 J ( θ 0 ) − J ( θ ) < 0

即

J(ηv⃗ ∇J(θ)<0 J ( η v → ∇ J ( θ ) < 0

因为 η η 是一个常量可以忽略，则

J(v⃗ ∇J(θ<0) J ( v → ∇ J ( θ < 0 )

根据定义，要下降的最快，则根据向量知识可以看出 v⃗  v → 必定与梯度方向 ∇J(θ) ∇ J ( θ ) 反向，则有

v⃗ =−∇J(θ)∣∣∇J(θ)∣∣ v → = − ∇ J ( θ ) ∣ ∣ ∇ J ( θ ) ∣ ∣

所以带入上式有

θ0≈θ−η∣∣∇J(θ)∣∣∇J(θ) θ 0 ≈ θ − η ∣ ∣ ∇ J ( θ ) ∣ ∣ ∇ J ( θ )

∣∣∇J(θ)∣∣ ∣ ∣ ∇ J ( θ ) ∣ ∣ 是一个标量，所以可以另

θ　=　θ0−α∇f(θ0) θ 　 = 　 θ 0 − α ∇ f ( θ 0 )

repeat until convergence{

θj　=　θj−α∇f(θj)(forveryj) θ j 　 = 　 θ j − α ∇ f ( θ j ) ( f o r v e r y j )

}

重复以上过程则可以得到我们所需要的 θ θ 值。

接下来对 ∇f(θ) ∇ f ( θ ) 进行求解

∂J(θ)∂θj=1m(hθ(x)−y)∗∂∂θj(hθ(x)−y) ∂ J ( θ ) ∂ θ j = 1 m ( h θ ( x ) − y ) ∗ ∂ ∂ θ j ( h θ ( x ) − y )

∂J(θ)∂θj=1m(hθ(x)−y)∗∂∂θj(∑i=0mθixi−yi) ∂ J ( θ ) ∂ θ j = 1 m ( h θ ( x ) − y ) ∗ ∂ ∂ θ j ( ∑ i = 0 m θ i x i − y i )

∂J(θ)∂θj=1m(hθ(x)−y)xi ∂ J ( θ ) ∂ θ j = 1 m ( h θ ( x ) − y ) x i

所以上式可更新为

θj:=θj+αm∑i=1m(yi−hθ(xi))xij θ j := θ j + α m ∑ i = 1 m ( y i − h θ ( x i ) ) x j i

以上式子通过多次计算即可算出对应的最佳 θ θ 值

注意， α α 的取值不能过大也不能过小，过小则梯度下降的速率很慢，过大则拟合效果很差甚至使损失函数越变越大。若想要得到 α α 的最佳取值，则可以多次选取不同的 α α 值，计算出对应的损失函数，若损失函数在变小，则优化方式有效(通常以三的倍数或者十的倍数取值eg.0.01,0.03.0.1,0.3,1)。同时该算法算出的不一定的全局最小值，而是局部最小值，由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。

当梯度下降到一定数值后，每次迭代的变化很小，这时可以设定一个阈值，只要变化小于该阈值，就停止迭代，而得到的结果也近似于最优解。

在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据进行归一化（normalization）处理。通常是求出其期望 x¯¯¯ x ¯ 和标准差std(x),然后利用公式

x−x¯¯¯std(x) x − x ¯ s t d ( x )

算出新的特征进行计算

矩阵表示及计算

这里通过矩阵运算可以简化原始的方案，设计如下：

X=∣∣∣∣∣∣∣−(x(1))T−−(x(2))T−⋮−(x(m))T−∣∣∣∣∣∣∣Y=∣∣∣∣∣∣∣y(1)y(2)⋮y(m)∣∣∣∣∣∣∣ X = | − ( x ( 1 ) ) T − − ( x ( 2 ) ) T − ⋮ − ( x ( m ) ) T − | Y = | y ( 1 ) y ( 2 ) ⋮ y ( m ) |

易得其中Ｘ为m*(n+1)的矩阵，Y为m*１的矩阵
因为有 fθ(x)=θ0+θ1x1+θ2x2+…+θnxn f θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + … + θ n x n 所以由矩阵表示则有

fθ(x)=Xθ f θ ( x ) = X θ

误差函数则可以表示为

J(θ)=12m∑i=1m(fθ(xi)−yi)2＝12m(Xθ−Y)T(Xθ−Y) J ( θ ) = 1 2 m ∑ i = 1 m ( f θ ( x i ) − y i ) 2 ＝ 1 2 m ( X θ − Y ) T ( X θ − Y )

此时对 J(θ) J ( θ ) 求导可得

所以

∇J(θ)=1mXT(Xθ−Y) ∇ J ( θ ) = 1 m X T ( X θ − Y )

要想最小化损失函数，当 XtX X t X 为满秩矩阵或正定矩阵时，令

∇J(θ)＝０ ∇ J ( θ ) ＝ ０

则得到

θ=(XTX)−1XTY θ = ( X T X ) − 1 X T Y

这样就省略了前面计算的循环，简便了计算
然而，现实任务中 XTX X T X 往往不是满秩矩阵，此时求出多个 θ θ ，都能使均方误差最小化。选择哪一个解作为输出，将由学习算法的归纳偏好决定，常见的做法是引入正则化。

BGD，SGD，MBGD

批量梯度下降法（Batch Gradient Descent）

对于批量梯度下降法，其本质就是上面所讲的梯度下降算法，采用所有数据来梯度下降，所以速率会有所降低，其对应的更新公式是

θj:=θj+αm∑i=1m(yi−hθ(xi))xij θ j := θ j + α m ∑ i = 1 m ( y i − h θ ( x i ) ) x j i

随机梯度下降法（Stochastic Gradient Descent）

首先给出随机梯度下降法对应的更新公式

θj=θj+α(yi−hθ(xi))xij θ j = θ j + α ( y i − h θ ( x i ) ) x j i

很容易可以看出每次更新 θj θ j 时只需要一个样本来求梯度，这样可以大大提升运算的速率，但经常被噪声干扰得不到局部最优值.如果数据量非常大，比如m＝300,000,000则，使用批量梯度下降则收敛得会非常慢，计算开销很大。此时若使用随机梯度下降，则能够大大提升运算速率。
随机梯度下降相当于先打乱整个训练集的顺序，然后对于每一个训练样本计算他的代价函数，进行一小步梯度下降，修改 θ θ 值，使他对该样本拟合得好一点，然后再做下一个，直到完成对整个训练集的拟合。每次更新使得 θ θ 朝着全剧最小量前进一点，最终得到合适的 θ θ 值。
值得注意的是，随机梯度下降的过程中，其应该是在靠近全局最小量的某个范围内徘徊，而不是直接逼近全局最小量并停留在那里。

小批量梯度下降法（Mini-batch Gradient Descent）

给出小批量梯度下降法的更新公式

θj:=θj+αx∑i=tt+x−1(yi−hθ(xi))xij θ j := θ j + α x ∑ i = t t + x − 1 ( y i − h θ ( x i ) ) x j i

可以看出，小批量梯度下降法是BGD和SGD的折中考虑能更有效避免上面所说的问题，某些情况下能够更快的收敛到最小值。随机梯度下降每次只处理一个样本，而只处理一个样本没有太多的并行运算，所以有时一个好的向量化处理方法会比随机梯度下讲更加有效。
同时，为减少噪声，可以适当增大样本数量x/

以下是Octave的代码实现（数据来自吴恩达Coursera ex1）

clear;close all;clc
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y);
plot(X,y,'rx','MarkerSize',5);
ylabel('Profile in $10,000s');
xlabel('Popilation of city in 10,000');
%-------------------------------------------------
X = [ones(m, 1), data(:,1)];
alpha = 0.01;
interations = 1500;
theta = zeros(2,1);
%-------------------------------------------------
J = 0;
predictions=X*theta;
SqrErrors=(predictions-y) .^2;
J=1/(2*m)*sum(SqrErrors);
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 32.07\n');
%--------------------------------------------------
fprintf('\nGradient Descent ...\n')

J_history = zeros(interations, 1);
for iter = 1:interations,
    theta = theta - alpha/m*(X'* (X*theta - y));
    predictions=X*theta;
    SqrErrors=(predictions-y) .^2;
    J_history(iter)=1/(2*m)*sum(SqrErrors);
end

fprintf('Theta found by gradient descent:\n');
fprintf('%f\n', theta);
fprintf('Expected theta values (approx)\n');
fprintf(' -3.6303\n  1.1664\n\n');

%-------------------------------------------------
hold on;
%X(:,2)
plot(X(:,2),X*theta,'-');
hold off;

Plotting Data ...
With theta = [0 ; 0]
Cost computed = 32.072734
Expected cost value (approx) 32.07

Gradient Descent ...
Theta found by gradient descent:
-3.630291
1.166362
Expected theta values (approx)
 -3.6303
  1.1664