西南科技大学第十六届ACM程序设计竞赛暨绵阳市邀请赛 (补题计划)(思维，数学等等)

B.签到题(组合数学)
题目传送
题意:

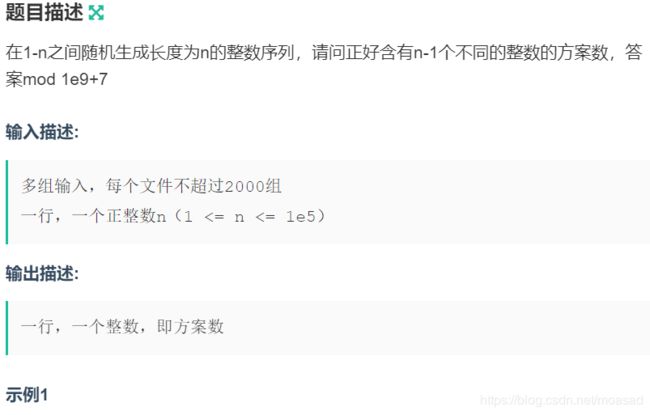
思路:
从n个数里面先选出n-1个数那么有n种选法。然后现在我们要构成n个数，所以必须有俩个数是一样的，现在再从n-1个数里面选出1个数，有n-1种选法那么现在有n*(n-1)种选法。然后现在的每一种选法中有n个数，那么就有n!/2种排法，因为有俩个数相同所以要除二。

这里要特别注意的是，如果多次操作大数取余，那么是很可能t掉的因为大数取余是很耗时间的，所以我们还要先预处理n的阶乘

AC代码

#include 
inline long long read(){char c = getchar();long long x = 0,s = 1;
while(c < '0' || c > '9') {if(c == '-') s = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x*10 + c -'0';c = getchar();}
return x*s;}
using namespace std;
#define NewNode (TreeNode *)malloc(sizeof(TreeNode))
#define Mem(a,b) memset(a,b,sizeof(a))
#define lowbit(x) (x)&(-x)
const int N = 1e5 + 10;
const long long INFINF = 0x7f7f7f7f7f7f7f;
const int INF = 0x3f3f3f3f;
const double EPS = 1e-7;
const long long mod = 1e9+7;
const double II = acos(-1);
const double PP = (II*1.0)/(180.00);
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> piil;
signed main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    ll n,arr[N] = {0};
    arr[0] = 1;
    for(int i = 1;i <= N;i++) arr[i] = arr[i-1] * i % mod;
    while(cin >> n)
    {
        ll sum = (n*(n-1)/2) % mod * arr[n] % mod;
        cout << sum << endl;
    }
}

C.救救AR(思维，构造)
题目传送

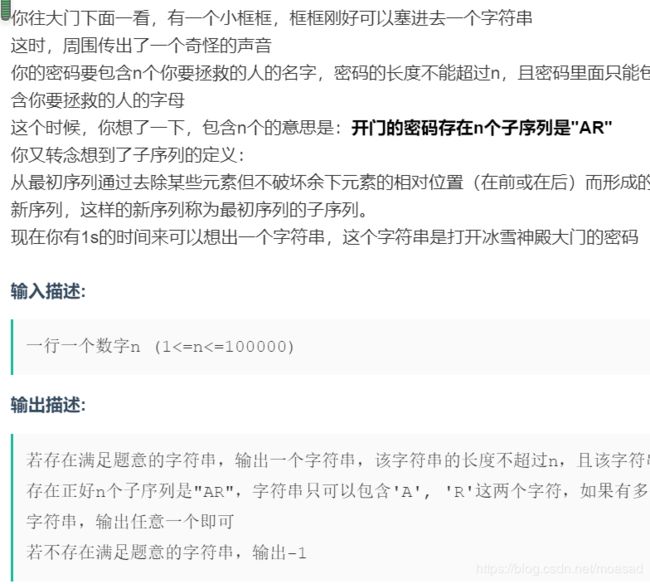
思路:
1.当n小于4的时候直接输出-1。

2.当n为偶数时，那么我们直接把n拆成2*(n/2)即可，即输出俩个’A’，然后(n/2)个’R’。

3.当n为奇数时，我们先输出一个"AR"，然后此时还差n-1个子序列，这时的n-1为偶数，那么又回到的了情况2，但是这时候要少输出一个’A’ 。

AC代码

#include 
inline long long read(){char c = getchar();long long x = 0,s = 1;
while(c < '0' || c > '9') {if(c == '-') s = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x*10 + c -'0';c = getchar();}
return x*s;}
using namespace std;
#define NewNode (TreeNode *)malloc(sizeof(TreeNode))
#define Mem(a,b) memset(a,b,sizeof(a))
#define lowbit(x) (x)&(-x)
const int N = 1e5 + 10;
const long long INFINF = 0x7f7f7f7f7f7f7f;
const int INF = 0x3f3f3f3f;
const double EPS = 1e-7;
const long long mod = 1e9+7;
const double II = acos(-1);
const double PP = (II*1.0)/(180.00);
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> piil;
signed main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int n;
    cin >> n;
    if(n < 4) cout << -1 << endl;
    else if(n % 2 == 0)
    {
        cout << "AA";
        for(int i = 0;i < n/2;i++)
            cout << 'R';
        cout << endl;
    }
    else
    {
        cout << "ARA";
        for(int i = 0;i < n/2;i++)
            cout << 'R';
        cout << endl;
    }
}

E.呼兰河传(思维)
题目传送
题意:

思路:
很明显所有数的最小公倍数肯定是最大的，但是每一个数依次求最小公倍数肯定要t，而且每一个数求最小公倍数再取模，肯定会导致答案错误。
所以我们要换一种其他的方法:我们把每一个数质因数分解，然后统计每一个质因数最多的次数，最后再用一个快速幂(可以防止爆数据)，把所有质因数的幂次方求出来就可以了

我们可以看到(1 <= n <= 1e6,1 <= a[i] <= 1e5)所以肯定有不少重复的，可以选择去重后再算，这样会快很多。如果不去重，简直是在边缘徘徊，如果我的函数调用不加inline，那么就直接t了。。。。或者直接不用函数调用，直接在主函数写也可以。

AC代码

#include 
inline long long read(){char c = getchar();long long x = 0,s = 1;
while(c < '0' || c > '9') {if(c == '-') s = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x*10 + c -'0';c = getchar();}
return x*s;}
using namespace std;
#define NewNode (TreeNode *)malloc(sizeof(TreeNode))
#define Mem(a,b) memset(a,b,sizeof(a))
#define lowbit(x) (x)&(-x)
const int N = 1e5 + 10;
const long long INFINF = 0x7f7f7f7f7f7f7f;
const int INF = 0x3f3f3f3f;
const double EPS = 1e-7;
const long long mod = 1e9+9;
const double II = acos(-1);
const double PP = (II*1.0)/(180.00);
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> piil;
ll vis[N],sum = 1;
ll quick_pow(ll a,ll b)//这里加了个inline就t了。。不知道为啥，所以还是去重叭。。。
{
    ll ans = 1;
    while(b)
    {
        if(b&1) ans = ans * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return ans;
}
inline void solve(ll a)
{
    for(ll i = 2;i * i <= a;i++)
    {
        if(a % i == 0)
        {
            ll num = 0;
            while(a % i == 0)
                num++,a /= i;
            vis[i] = max(vis[i],num);
        }
    }
    if(a > 1) vis[a] = max(vis[a],(ll)1);
}
signed main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    ll n;
    n = read();
    for(ll i = 0,a;i < n;i++)
    {
        a = read();
        solve(a);
    }
    for(ll i = 1;i <= 1e5;i++)
        sum = sum * quick_pow(i,vis[i]) % mod;
    printf("%lld\n",sum);
}

暂时补到这。。。