[以太坊源代码分析] IV. 椭圆曲线密码学和以太坊中的椭圆曲线数字签名算法应用
数字签名算法在Ethereum中的应用不少,目前已知至少有两处:一是在生成每个交易(Transaction, tx)对象时,对整个tx对象进行数字签名;二是在共识算法的Clique算法实现中,在针对新区块进行授权/封印的Seal()函数里,对新创建区块做了数字签名。这两处应用的签名算法都是椭圆曲线数字签名加密算法(Elliptic Curve Digital Signature Algorithm,ECDSA)。Ethereum 在采用ECDSA进行数字签名的基础上,基于自身的业务需求,又将数字签名过程所用的公钥作为地址类型(common.Address)对象,在许多应用场景下作为地址(即账户的唯一标识符)使用。
有关ECDSA的几个理论概念的关系是这样的:椭圆曲线数字加密算法ECDSA是数字签名算法(DSA)的变例之一,ECDSA的基础是椭圆曲线密码学(Elliptic-curve cryptography,ECC),而ECC的理论前提是椭圆曲线上点的倍积(Elliptic curve point multiplication)。本文将从这些概念的原理讲起,试图讲解一下Ethereum所采用ECDSA的来龙去脉。
1.椭圆曲线点的倍积
概念知识
椭圆曲线的点倍积(point multiplication),指的是椭圆曲线上一个点沿着这条曲线不断的与自身相加,最终落在曲线另一个点上的(计算)过程。也许有些地方会把这里的multiplication翻译成“乘积”或“乘法”,那样的话就要特别注意,这种所谓的“点乘积”,是特指一个标量与一个点的乘积,它属于一种标量乘法(scalar multiplication)。所以,个人觉得将这里的point multiplication翻译成“点倍积”会更准确些,本文会沿用这种翻译。
假设起点是椭圆曲线点P,终点是曲线上点R,于是我们有如下点倍积公式,注意此时标量一定要写在点的左边。
R = nP
上式中的结果R点暂时还计算不出来,我们需要多一些准备。理论上,这里的椭圆曲线所选择的几何方程是固定的,它可以表示为:
y^2 = x^3 + ax + b
上式中a和b都是普通标量参数,以上方程所绘出的几何曲线如下图所示,其中红色曲线表示(a, b) = (-7, 6)时的椭圆曲线,蓝色曲线表示 (a, b) = (-6, 6)时的椭圆曲线。显然,a和b的取值对曲线形状还是有影响的。
现在有了椭圆曲线的具体形状和方程,假设曲线上有一个点P,我们想计算它的倍积nP,该怎么做呢?
这里需要再引入一个概念:椭圆曲线点的相加(point addition)。以上图为例,红色椭圆曲线上有两个点P和Q,设定这两个点相加得到一个同样处于曲线上的R点,这个R点来自P, Q两点直连延长线与椭圆曲线的交点(T点)的共轭点,也就是T点沿X轴的对称点R。由于上述椭圆曲线本身必定沿X轴对称,所以这个R点也必定处于曲线上。
我们从代数的角度重新看下这个问题:
这里我们用XY坐标来表示P,Q,R每个点,结合设定的椭圆曲线公式 y^2 = x^3 + ax + b,可以得到如下解答:
通过引入一个参数lambda,我们可以得到P,Q两点相加得到R点的坐标。
很好,我们再往前跨出一步,如果P点和Q点重合,那么它们相加R点是怎样的呢?这种情况被称之为椭圆曲线点的翻倍或叠加(point double),根据上式,R点的x,y相对坐标不变,我们只需要用一个特殊的lambda值就行了,不过要留意此时的lambda取值跟曲线方程参数a有关:
好的,在拥有了以上这些基础知识之后,我们终于可以计算出椭圆曲线点的倍积,因为对于 R = nP,无论n取何值,我们都可以通过上述“点相加”和“点翻倍”的方法计算出R点坐标。
计算方法
我们来看下具体的如何计算椭圆曲线点倍积 Q = dP,即已知椭圆曲线点P和标量d,计算出曲线点Q。
开始写代码前需要将标量d以二进制的方式表示出来,以便于应用“点相加”和“点翻倍”方法。
上式就是d的二进制表示,代码中将各个系数表示成一个长度为(m+1)的数组d[]即可,d[i]对应于第i个bit位的取值0或1。下列伪代码均来自wiki-PointMultiplication。
最直观的就是迭代型的,比如自底向上的迭代:
// iterative: index increasing
N = P; Q = 0;
for i in [0, m] do:
if d[i] == 1 then Q = point_add(Q, N)
N = point_double(N)
return Q// iterative: index decreasing
Q = 0;
for i in [m, 0] do:
Q = point_double(Q)
if d[i] == 1 then Q = point_add(Q,P)
return Q
除了迭代型,当然还有递归型的
// recursive
func f(p, n) is
if n == 0 then
return 0
else if n == 1 then
return p
else if n mod(2) == 1 then
return point_add(p, f(p, n-1))
else
return f(point_double(p), n/2)
这样得到的m更小,也就是系数数组d[]的长度更小,这就意味着仅需更少的迭代(递归)次数。相关伪代码可见wiki。
2. 椭圆曲线密码学
椭圆曲线密码学(Elliptic-curve cryptography,ECC)同当前流行的其他几种密码学类型,也是通过一个公钥 + 一个私钥组成的一对钥匙来进行加密相关操作。它基于有限域上特定椭圆曲线进行操作,最重要的操作是椭圆曲线的点倍积,不夸张的说,椭圆曲线点倍积正是椭圆曲线密码学的基石。
为什么这么说呢?因为对于点倍积的计算式Q = nP 而言, 在已知起点P和终点Q的情况下,想要计算出n,理论上在目前计算条件下近乎是不可能的!这个数学证明过程比较复杂,这里只想举一个极端的例子。回看上一章节中那幅图,如果这里选用了图中红色椭圆曲线作点倍积运算,注意到它的左边部分是一个封闭的不规则圆弧,如果倍积运算的终点Q恰好落在这个圆弧上面,那么参数n是死活都算不出来的,因为如果增大n,让Q在圆弧上多循环几圈后依旧保持在Q点...
加密用椭圆曲线的参数组
ECC的使用场景包括数字签名,安全的伪随机数生成等。在应用中,所采用的椭圆曲线必须用一组完整的参数来加以定义,这组参数被称为域参数。一般的,ECC定义的这组参数可表为
(p, a, b, G, n, h)
其中 p 是一个极大的质数,用来表示曲线所有点的范围; a, b 分别是椭圆曲线方程 y^2 = x^3 + ax + b 中的系数;G 是该椭圆曲线上点倍积的基点,对于所有通过点倍积运算得到的曲线上点的集合来说,G可算是它们的生成器(generator);n 是基点G的可倍积阶数,定义为能够使得点倍积nG 不存在的最小的整数n;h 是一个整数常量,它跟椭圆曲线运算中得到点的集合以及 n 有关,h 一般取值为1。
在下一章节中,我们可以看到这些椭圆曲线参数在椭圆曲线数字签名中的应用。
3. 椭圆曲线数字签名算法理论
椭圆曲线数字签名算法(ECDSA)是数字签名算法(DSA)的变例之一,它基于椭圆曲线密码学。相比于基于RSA密码学的DSA,ECDSA在计算数字签名时所需的公钥长度可以大大缩短。比如,对于一项安全级别为80 bits的数字签名来说,ECDSA需要的公钥长度仅仅为安全级别的2倍,即160 bits,而同样安全级别要求下的RSA所需公钥长度至少为1024 bits;同时算法所生成的签名长度,不论是ECDSA还是RSA都大约是320 bits,这样一来,ECDSA相对于RSA在应用上的优势就很明显了。
注:安全级别(security level)的概念是:N bits的安全级别,意味着攻击者大约要经过2^N的运算才能获得本次加密用的私钥。安全级别所代表的bits越长,意味着安全性能越好,越难以被攻破,当然同时在加密时的代价,包括公钥长度和生成签名长度,自然也会相应增加。
ECDSA基于DSA,DSA定义了数字签名生成过程和验证过程的基本步骤,通过比较可以看出,ECDSA遵循了DSA的这些定义,并在一些特定步骤中,转而采用了椭圆曲线的相关操作。这里由于篇幅所限,就不详细介绍DSA的内容了,有兴趣的朋友可以去wiki上一看。
数字签名的生成
下面来看一下ECDSA的签名生成过程,以下内容主要来自wiki_ECDSA
假设Alice要给Bob发一个经过数字签名的消息,他们首先需要定义一组共同接受的椭圆曲线加密用参数,简单的,这组参数可表示为
(CURVE, G, n)
其中,CURVE表示椭圆曲线点域和几何方程;G是所有点倍积运算的基点;n是该椭圆曲线的可倍积阶数(multiplicative order),作为一个很大的质数,n的几何意义在于,nG = 0,即点倍积nG的结果不存在,而对于小于n的任何一个正整数 m = [1,n-1],点倍积mG都可以得到一个合理的处于该椭圆曲线上的点。
其次,Alice要创建一对钥,即一个私钥和一个公钥。私钥来自于[1, n-1]范围内一个随机数:
公钥如下,它来自私钥和基点的椭圆曲线点倍积:
好,准备工作就绪,假设Alice想要对消息m作数字签名,有以下步骤:
- 计算 e = HASH(m),HASH是一个哈希加密函数,比如SHA-2,或SHA-3。
- 计算 z,来自e的二进制形式下最左边(即最高位)L_n个bits,而L_n是上述椭圆曲线参数中的可倍积阶数n的二进制长度。注意z 可能大于n,但长度绝对不会比 n 更长。
- 从 [1, n-1] 内,随机选择一个符合加密学随机安全性的整数k。
- 计算一个椭圆曲线上点:
- 以下式计算 r 值, 如果r == 0, 则返回步骤3重新计算。
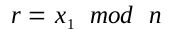
- 以下式计算 s 值,如果 s == 0,则返回步骤3重新计算。
- 生成的数字签名就是 (r, s)
特别需要注意的是步骤3中 k 的选择,它不仅要满足加密学的随机安全性要求,要像私钥一样保护起来,更重要的是,在每次生成一个新的数字签名时,这个 k 必须每次都要更新。否则,通过上述数字签名过程中的算式相互换算,很容易从中破译出私钥!具体换算过程可见wiki_ECDSA。
数字签名的验证
对于消息的接收方Bob来说,他除了收到数字签名文件外,还会有一份公钥。所以Bob的验证分两部分,首先验证公钥,然后验证签名文件(r, s)。
公钥的验证
- 公钥
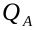 的坐标应是有效的,不会等于一个极限值空点
的坐标应是有效的,不会等于一个极限值空点
- 通过公钥
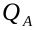 的坐标验证它必须是处于该椭圆曲线上的点。
的坐标验证它必须是处于该椭圆曲线上的点。 - 应有下式成立,即曲线的可倍积阶数 n 与公钥的点倍积不存在
签名文件的验证
- 验证 r 和 s 均是处于[1, n-1]范围内的整型数;否则验证失败
- 计算 e = HASH(n),HAHS()即签名生成过程步骤1中使用的哈希函数。
- 计算 z,来自 e的最左边L_n个bits。
- 计算参数 w:
- 计算两个参数 u1 和 u2:
- 计算(x1, y1),如果(x1, y1)不是一个椭圆曲线上的点,则验证失败:
- 如果以下恒等式不成立,则验证失败:

以上就是椭圆曲线数字签名算法(ECDSA)的生成和验证的完整过程,在wiki_ECDSA还可以看到关于上述验证方法正确性的证明过程。无论用何种编程语言实现,其中数字签名的生成和验证必然要遵循以上的理论和步骤。
4. go-ethereum中的椭圆曲线数字签名算法
go语言安装包中自带的crypto/ecdsa包中包含了关于椭圆曲线的结构体声明和操作函数,以及ECDSA的签名生成和验证到的完整实现代码。不过,以太坊(go-ethereum)并没有采用这个crypto/ecdsa包来实现它自己的数字签名算法。尽管如此,这部分代码仍然很有阅读的必要,原因有二:1.它里面定义的一些行为接口和结构体类型,依然在被go-ethereum中的代码所使用,以方便调用;2. 它关于ECDSA的实现代码写的简洁清晰,非常适合ECDSA的初学者加以研习。
go语言包中的ecdsa代码包
go语言包自带的crypto/ecdsa相关的结构体如以下UML图所示:
对照着上一章节中ECDSA的算法理论,以上的结构体和接口的声明就非常易于理解了。
- ecdsa.PublicKey结构体通过持有一个elliptic,Curve接口的实现体,可以提供椭圆曲线的所有属性,和相关操作;PublicKey的成员(X,Y),对应于算法理论中公钥
 的坐标。
的坐标。 - elliptic.Curve接口声明了椭圆曲线的相关操作方法,其中Add()方法就是椭圆曲线点倍积中的“点相加”操作,Double()就是点倍积中的“点翻倍”操作,ScalarMult()根本就是一个点倍积运算(参数k是标量),IsOnCurve()检查参数所代表的点是否在该椭圆曲线上;
- elliptic.CurveParams结构体实现了
接口的所有方法,另外用成员属性定义了一个具体的椭圆曲线,比如(Gx, Gy) 表示该椭圆曲线的基点,即算法理论中的G点; N 是与基点对应的可倍积阶数n;B是椭圆曲线几何方程中的参数b,注意此处ecdsa代码包中隐含的椭圆曲线方程为y^2 = x^3 - 3x + b,故只需一项参数b即可。 - ecdsa.PrivateKey是暴露给外部使用的主要结构体类型,它其实是算法理论中的私钥和公钥的集合。它的成员D,才真正对应于算法理论中的(标量)私钥
 。
。 - ecdsa.ecdsaSignature对应于生成的数字签名(r, s)。
由此可见,go语言自带的crypto/ecdsa代码包从结构体的成员到方法的声明,都力图使得其所代表的ECDSA算法理论清晰易懂。关于实现函数,重点推荐ecdsa/ecdsa.go中的两个函数Sign()和Verify()
// go-1.x/src/crypto/ecdsa/ecdsa.go
func Sign(rand io.Reader, priv *PrivateKey, hash []byte) (r, s *big.Int, err error)
func Verify(pub *PublicKey, hash []byte, r, s *big.Int) bool
go-ethereum中对ECDSA的调用
go-ethereum中实际采用的ECDSA函数实现,来自于第三方库libsecp256k1,它是一个C++库,在比特币代码(github_bitcoin)中就有应用,被视为一个经过优化的,针对椭圆曲线secp256k1的一个实现库。secp256k1对应于一组特定的椭圆曲线数字签名参数,包括曲线方程以及签名运算所需的一系列参数等,secp256k1被率先应用在比特币中,关于它的参数细节可见secp256k1,其中所指定的曲线方程为y^2 = x^3 + 7,它的形状如下图所示:
在go-ethereum源代码中,路径在/crypto/下的代码包负责所有与加密相关的操作,libsecp256k1库的源代码也在其中/secp256k1/的子路径下存放,待编译后以C++库文件的方式被调用。
处理数字签名
以go-ethereum中交易对象的代码为例,与ECDSA签名相关的操作,都被放在一个名叫Signer的接口以及它的实现体里了。
接口
Signer的三个实现类中,HomesteadSigner通过持有FrontierSigner对象,可以节省代码。关于EIP155: EIP(Ethereum Improvement Proposals,EIP)是Ethereum的需求汇总。EIP155是其中一个比较重要的需求,加入了一种抵御重现攻击(Replay Attack)的简单方法,要求在对tx作签名(或恢复签名时),在Hash(*Transaction)函数里的RLP编码环节多选择几个成员变量,所以EIP155Signer中的Hash()是重新定义的。
从数字签名中恢复出公钥(地址)
从数字签名中恢复(解析)出地址变量的函数叫recoverPlain():
// core/types/transaction_signing.go
func recoverPlain(sighash common.Hash, R, S, Vb *big.Int, homestead bool) (common.Address, error) {
V := byte(Vb.Uint64() - 27)
if !crypto.ValidateSignatureValues(V, R, S, homestead) {
return common.Address{}, ErrInvalidSig
}
// encode signature in uncompressed format
r, s := R.Bytes(), S.Bytes()
sig := make([]byte, 65)
copy(sig[32-len(r):32], r)
copy(sig[64-len(s):64], s)
sig[64] = V
// recover the public key from the signature
pub, err := crypto.Ecrecover(sighash[:], sig)
if err != nil || len(pub) == 0 || pub[0] != 4 {
return common.Address{}, err
}
// convert pubKey to Address
var addr common.Address
copy(addr[:], crypto.Keccak256(pub[1:])[12:])
return addr, nil
}首先调用crypto.ValidateSignatureValues()来验证数字签名是否正确有效,crypto包的这个方法正是通过调用libsecp256k1库的API,遵循ECDSA算法理论中有关数字签名验证部分来完成的;
其次,将R,S,V拼接出所需的数字签名字符串;
接着,调用crypto.Ecrecover(),凭借被数字签名的内容sighash和签名字符串sig,从中恢复出数字签名所用的公钥,当然,crypto包的方法依然调用libsecp256k1库的API来完成;
最后,在返回的公钥里,去掉标志头所在的第一个byte(值为4),生成它的SHA-3(256 bits)哈希值,再截取其中的后20bytes,此即最终返回的Address类型变量。
生成数字签名
针对某个tx对象生成数字签名的函数叫SignTx()
// core/types/transaction_signing.go
func SignTx(tx *Transaction, s Signer, prv *ecdsa.PrivateKey) (*Transaction, error) {
h := s.Hash(tx)
sig, err := crypto.Sign(h[:], prv)
if err != nil {
return nil, err
}
return tx.WithSignature(s, sig)
}// /crypto/signature_cgo.go
func Sign(hash []byte, prv *ecdsa.PrivateKey) (sig []byte, err error) {
if len(hash) != 32 {
return nil, fmt.Errorf(...) // hash must be 32 bytes
}
seckey := math.PaddedBigBytes(prv.D, n:prv.Params().BitSize/8)
defer zeroBytes(seckey)
return secp256k1.Sign(hash, seckey)
}可见crypto.Sign()函数正是通过调用libsecp256k1库的API来完成椭圆曲线数字签名的生成。
公钥和地址
以太坊中用到的Address类型地址变量,比如每个账户的地址,都来自于椭圆曲线数字签名用的公钥。在数字签名中,公钥可以在多次签名中重复使用,这反映到以太坊的账户上,就是一个账户下的多次交易,即多个不同的Transaction对象,它们所作的数字签名均使用同一个公钥。
具体到变量类型上,Address类型是一个长度为20 bytes的字符串,而椭圆曲线数字签名中的公钥,原生含义应该是曲线上的一个点的坐标(X, Y),那么它们之间必然存在格式上的相互转换。在代码中,这涉及到三种不同格式(类型):地址变量是Address类型,长度为20bytes的字符串;publicKey变量是一个字符串,长度未知;椭圆曲线上的公钥,是一个点的坐标,在ecdsa.PublicKey{}中以成员X,Y表示。
publicKey变量转换成Address类型,在之前提到的core.types.recoverPlain()函数体里介绍过(函数末尾)。
publicKey字符串类型和ecdsa.PublicKey{}类型的格式转换函数,由crypto代码包定义。
// crypto/crypto.go
func ToECDSAPub(pub []byte) *ecdsa.PublicKey {
x, y := elliptic.Unmarshall(S256(), pub)
return &ecdsa.PublicKey{Curve:S256(), X:x, Y:y}
}
func FromECDSAPub(pub *ecdsa.PublicKey) []byte {
return elliptic.Marshall(S256(), pub.X, pub.Y)
}
ps, 上述代码中的S256(),是本地代码写的一个转换函数,返回一个elliptic.Curve接口的实现类,它基于secp256k1的椭圆曲线参数,自己实现了
小结:
- 以太坊中的数字签名全部采用椭圆曲线数字加密算法(ECDSA), 它的理论基础是椭圆曲线密码学(ECC),而ECC存在的理论基础是点倍积(point multiplication)算式 Q = dP 中的私钥 d (几乎)不可能被破译。ECC相对于基于大质数分解的RSA,在提供相同安全级别的情况下,仅需长度更短的公钥。
- 以太坊中调用的椭圆曲线数字签名算法实现,来自己libsecp256k1库,这是一个针对特定椭圆曲线secp256k1的、经过优化的C++库,并早已被比特币系统采用。
- 以太坊中的使用的Address类型,比如每个账户的地址,均来自于椭圆曲线数字签名的公钥。
![[以太坊源代码分析] IV. 椭圆曲线密码学和以太坊中的椭圆曲线数字签名算法应用_第1张图片](http://img.e-com-net.com/image/info8/2c96d0b6e3864d2a9a0a568947827cf8.jpg)

![[以太坊源代码分析] IV. 椭圆曲线密码学和以太坊中的椭圆曲线数字签名算法应用_第2张图片](http://img.e-com-net.com/image/info8/e7faed2bb47c43e1bb95938c73397ab2.jpg)
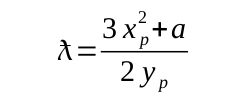
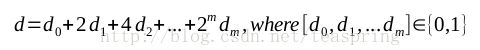
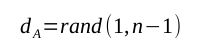


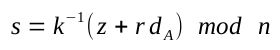
![[以太坊源代码分析] IV. 椭圆曲线密码学和以太坊中的椭圆曲线数字签名算法应用_第3张图片](http://img.e-com-net.com/image/info8/2ec1aaf11c5f4d169527dea5f9da51a1.jpg)
![[以太坊源代码分析] IV. 椭圆曲线密码学和以太坊中的椭圆曲线数字签名算法应用_第4张图片](http://img.e-com-net.com/image/info8/eee1e923ddd74dd4a4902e218c8e6a17.png)
![[以太坊源代码分析] IV. 椭圆曲线密码学和以太坊中的椭圆曲线数字签名算法应用_第5张图片](http://img.e-com-net.com/image/info8/c47b0035387140929bcea014d2823fb4.jpg)