算法设计与分析分支限界算法之迷宫问题
分支限界算法之迷宫问题
问题描述
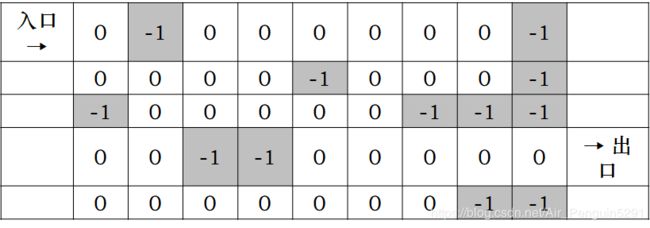
如下图所示,给出一个N*M的迷宫图和一个入口、一个出口。
编一个程序,打印一条从迷宫入口到出口的路径。这里黑色方块的单元表示走不通(用-1表示),白色方块的单元表示可以走(用0表示)。只能往上、下、左、右四个方向走。如果无路则输出“no way.”。
算法分析
只要输出一条路径即可,所以是一个经典的回溯算法问题,本例给出了回溯(深搜)程序和广搜程序。实现见参考程序。
代码
【深搜参考程序】
【深搜参考程序】
#include
using namespace std;
int n,m,desx,desy,soux,souy,totstep,a[51],b[51],map[51][51];
bool f;
int move(int x, int y,int step){
map[x][y]=step; //走一步,作标记,把步数记下来
a[step]=x; b[step]=y; //记路径
if ((x==desx)&&(y==desy)) {
f=1; totstep=step;
}
else {
if ((y!=m)&&(map[x][y+1]==0)) move(x,y+1,step+1); //向右
if ((!f)&&(x!=n)&&(map[x+1][y]==0)) move(x+1,y,step+1); //往下
if ((!f)&&(y!=1)&&(map[x][y-1]==0)) move(x,y-1,step+1); //往左
if ((!f)&&(x!=1)&&(map[x-1][y]==0)) move(x-1,y,step+1); //往上
}
}
int main(){
int i,j;
cin>>n>>m; //n行m列的迷宫
for (i=1;i<=n;i++) //读入迷宫,0表示通,-1表示不通
for (j=1;j<=m;j++)
cin>>map[i][j];
cout<<"input the enter:";
cin>>soux>>souy; //入口
cout<<"input the exit:";
cin>>desx>>desy; //出口
f=0; //f=0表示无解;f=1表示找到了一个解
move(soux,souy,1);
if (f) {
for (i=1;i<=totstep;i++) //输出直迷宫的路径
cout< 【广搜参考程序】
#include
using namespace std;
int u[5]={0,0,1,0,-1},
w[5]={0,1,0,-1,0};
int n,m,i,j,desx,desy,soux,souy,head,tail,x,y,a[51],b[51],pre[51],map[51][51];
bool f;
int print(int d){
if (pre[d]!=0) print (pre[d]); //递归输出路径
cout<>n>>m; //n行m列的迷宫
for (i=1;i<=n;i++) //读入迷宫,0表示通,-1表示不通
for (j=1;j<=m;j++)
cin>>map[i][j];
cout<<"input the enter:";
cin>>soux>>souy; //入口
cout<<"input the exit:";
cin>>desx>>desy; //出口
head=0;
tail=1;
f=0;
map[soux][souy]=-1;
a[tail]=soux; b[tail]=souy; pre[tail]=0;
while (head!=tail) { //队列不为空
head++;
for (i=1;i<=4;i++) { //4个方向
x=a[head]+u[i]; y=b[head]+w[i];
if ((x>0)&&(x<=n)&&(y>0)&&(y<=m)&&(map[x][y]==0)) { //本方向上可以走
tail++;
a[tail]=x; b[tail]=y; pre[tail]=head;
map[x][y]=-1;
if ((x==desx)&&(y==desy)) { //扩展出的结点为目标结点
f=1;
print(tail);
break;
}
}
}
if (f) break;
}
if (!f) cout<<"no way."<