leetcode中的二叉树经典问题(二)
每一个类型的数据结构题目一般都有该数据结构特征所带来的解决秘诀。对于二叉树来说,最大的宝典莫过于递归。
前面已经探讨了二叉树前中后三种遍历的递归和非递归方式。具体请看leetcode中的二叉树经典问题(一)。今天来说说二叉树的其他经典问题。
leetcode110判断一棵树是否为平衡二叉树https://leetcode.com/problems/balanced-binary-tree/
leetcode98判断一棵树是否为二叉搜索树https://leetcode.com/problems/validate-binary-search-tree
leetcode222完全二叉树的结点个数https://leetcode.com/problems/count-complete-tree-nodes/
附带:判断一个树是否为完全二叉树的代码。
下面进入正题。
判断一棵树是否为平衡二叉树
平衡二叉树的定义:二叉树的左右子树的高度差的绝对值不超过1.
解决思路: 由平衡二叉树的定义我们可以get到关键点:左右子树的高度以及左右子树的高度差 。利用递归的思想判断每一个结点的左右子树是否平衡,进而可以判断整一棵二叉树是否平衡。代码如下:
public static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public static boolean isBalanced(TreeNode root) {
if (root == null) return true;
boolean[] res = new boolean[1];
res[0] = true;
getHeight(root, 1, res);
return res[0];
}
private static int getHeight(TreeNode root, int level, boolean[] res) {
if (root == null) return level;
int lh = 0;
int rh = 0;
lh = getHeight(root.left, level + 1, res);
if (!res[0]) return level;
rh = getHeight(root.right, level + 1, res);
if (!res[0]) return level;
int height = Math.abs(lh - rh);
if (height > 1) res[0] = false;
return Math.max(lh, rh);
}
利用先序数组和中序数组构建还原出二叉树
一个先序数组和中序数组能够唯一确定一棵二叉树。对于先序遍历而言,每一棵树(包括子树)的父结点一定是先于左右孩子结点出现的;而对于中序遍历,左子树的所有结点先于父节点出现,基于这些特征,可以发现,先序数组中出现的第一个结点(对应数字1)在中序数组中出现的位置(1在index=3的位置出现)的左边就是该结点的左子树,右边就是该结点的右子树,下面画个图为了帮助大家更好的理解(对于图中的指针往下有解释)。
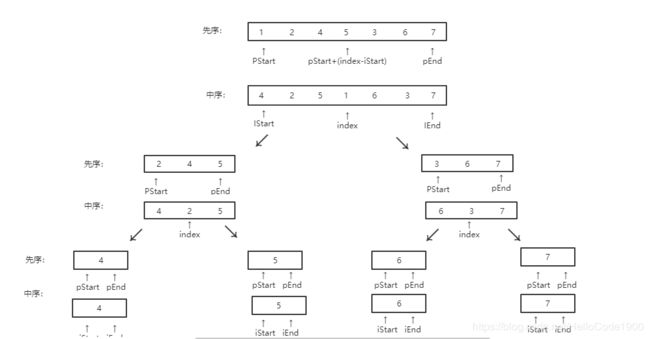
由上面的图看出,可以用递归还原整个构建的过程。在写代码之前,需要搞明白以下的三个问题:
- 在递归过程中,先序遍历的左右子树的边界在哪里?
- 中序遍历的左右子树的边界在哪?
- 递归的终止条件是什么?
前面我们说过,在中序遍历中,左子树会先于父结点出现。拿图中的例子来说,中序数组中数值为1的结点的左边都是该结点的左子树(即数值4,2,5对应的结点),通过简单计算可以得出该结点的左子树个数为(index-iStart)个。所以:
对于先序数组而言左子树的取值范围为[pStart,pStart+(index-iStart)],右子树的取值范围为[pStart+(index-iStart)+1,pEnd].
对于中序数组而言,左子树的取值范围为[iStart,index-1],右子树的取值范围为index+1,iEnd].
当先序数组的开始和结束指针相碰时,递归结束
如果理解了上面的分析,理解代码就很简单了。注意:代码实现过程中,利用HashMap存储中序遍历中每一个结点的数组下标位置(即index的位置),从而避免通过遍历数组寻找index的过程,起到优化的效果。
public static TreeNode buildTree_v1(int[] preorder, int[] inorder){
if(preorder==null|| inorder==null)return null;
HashMap<Integer,Integer> map = new HashMap<Integer, Integer>();
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return preInorder(preorder,0,preorder.length-1,inorder,0,inorder.length-1,map);
}
private static TreeNode preInorder(int[] preorder, int pStart, int pEnd, int[] inorder, int iStart, int iEnd, HashMap<Integer, Integer> map) {
if(pStart>pEnd) return null;
int index = map.get(pStart);//如果不用hashmap存储,这一步需要通过遍历的方式去寻找对应的下标。
TreeNode head = new TreeNode(index);
head.left = preInorder(preorder,pStart+1,pStart+index-iStart,inorder,iStart,index-1,map);//这几个参数参考上面分析中的左子树边界范围
head.right = preInorder(preorder,pStart+index-iStart+1,pEnd,inorder,index+1,iEnd,map);//这几个参数参考上面分析中的右子树边界范围
return head;
}
至此,就可以构建出完整的二叉树来了。类比这个还原过程,我们可以写出中序数组跟后续数组构建二叉树的代码了。
public static TreeNode buildTree_v2(int[] inorder, int[] postorder){
if(inorder==null|| postorder==null) return null;
HashMap<Integer,Integer> map = new HashMap<Integer, Integer>();
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return inPostOrder(inorder,0,inorder.length-1,postorder,0,postorder.length-1,map);
}
private static TreeNode inPostOrder(int[] inorder, int iStart, int iEnd, int[] postorder, int pStart, int pEnd, HashMap<Integer, Integer> map) {
if (pStart>pEnd) return null;
int index = map.get(pEnd);
TreeNode head = new TreeNode(pEnd);
head.left = inPostOrder(inorder,iStart,index-1,postorder,pStart,pStart+index-iStart-1,map);
head.right = inPostOrder(inorder,index+1,iEnd,postorder,pStart+index-iStart,pEnd-1,map);
return head;
}
两段代码的时间复杂度都是 O(n)。