隐马尔可夫模型(HHM)学习笔记1
隐马尔可夫模型简介
整理了李航和周志华书上的内容。
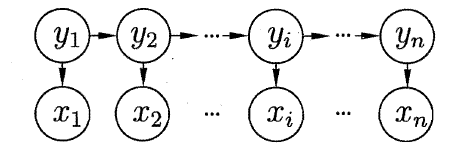
将隐马尔可夫模型中的变量分为两组:一组为状态变量 { y 1 , y 2 , … , y T } \left\{ {{y_1},{y_2}, \ldots ,{y_T}} \right\} {y1,y2,…,yT},其中 y i ∈ Y {y_i} \in {\Bbb Y} yi∈Y表示第 i i i时刻的系统状态,通常这个状态变量是隐藏的、不可观测的,因此状态变量也被称为隐变量。第二组变量是观测变量 { x 1 , x 2 , … , x n } \left\{ {{x_1},{x_2}, \ldots ,{x_n}} \right\} {x1,x2,…,xn},其中 x i ∈ X {x_i} \in {\Bbb X} xi∈X表示第 i i i时刻的观测值。状态变量 y i {y_i} yi在多个状态 { s 1 , s 2 , … , x N } \left\{ {{s_1},{s_2}, \ldots, {x_N}} \right\} {s1,s2,…,xN}之间切换,即 Y {\Bbb Y} Y的取值范围是 { s 1 , s 2 , … , s N } \left\{ {{s_1},{s_2}, \ldots ,{s_N}} \right\} {s1,s2,…,sN};观测变量在多个状态 { o 1 , o 2 , … , o M } \left\{ {{o_1},{o_2}, \ldots ,{o_M}} \right\} {o1,o2,…,oM}之间切换,即 X {\Bbb X} X的取值范围是 { o 1 , o 2 , … , o M } \left\{ {{o_1},{o_2}, \ldots ,{o_M}} \right\} {o1,o2,…,oM}。
如图表示了变量之间的依赖关系。在任意时刻,观测变量的取值仅依赖状态变量,即 x t x_t xt仅由 y t y_t yt确定,与其他状态变量的取值无关。同时, t t t时刻的状态变量仅依赖于 t − 1 t-1 t−1时刻的状态 y t − 1 {y_{t-1}} yt−1,与其余的状态变量无关。这就是“马尔科夫链”:系统的下一时刻的状态仅由当前状态决定,不依赖以往的任何状态。
除此之外,确定一个马尔科夫模型还需要三组参数:初始状态概率、状态转移概率以及输出观测概率。
初始状态概率:模型在初始时刻状态变量 y 1 y_1 y1为各个状态的概率,记为 Π = ( π 1 , π 2 , … , π N ) {\Pi } = \left( {{\pi _1},{\pi _2}, \ldots ,{\pi _N}} \right) Π=(π1,π2,…,πN),其中 π i = P ( y 1 = s i ) , 1 ⩽ i ⩽ N {\pi _i} = P\left( {{y_1} = s{}_i} \right),1 \leqslant i \leqslant N πi=P(y1=si),1⩽i⩽N表示模型的初始状态为 s i {s{}_i} si的概率。下文中也表示为 π y 1 = P ( y 1 = s i ) , 1 ⩽ i ⩽ N {\pi _{{y_1}}} = P({y_1} = {s_i}),1 \leqslant i \leqslant N πy1=P(y1=si),1⩽i⩽N。
状态转移概率:状态变量在各个状态转换的概率,记为矩阵 A = [ a i j ] N × N {\bf{A}} = {\left[ {{a_{ij}}} \right]_{N \times N}} A=[aij]N×N,其中 a i j = P ( y t + 1 = s j ∣ y t = s i ) , 1 ⩽ i , j ⩽ N {a_{ij}} = P\left( {{y_{t + 1}} = {s_j}|{y_t} = {s_i}} \right),1 \leqslant i,j \leqslant N aij=P(yt+1=sj∣yt=si),1⩽i,j⩽N表示任意时刻 t t t,若状态为 s i {{s_i}} si,则观测 o j {o_j} oj被获取的概率。下文中下标 i j ij ij会视情况而灵活变化,当 i i i变为 y t y_t yt时,表示此时的状态变量 y t = s i y_t=s_i yt=si;当 j j j变为 x t x_t xt时,表示此时的观测变量 x t = o j x_t=o_j xt=oj。
输出观测概率:在当前状态变量的前提下获取各个观测值的概率,记为矩阵 B = [ b i j ] N × M {\bf{B}} = {\left[ {{b_{ij}}} \right]_{N \times M}} B=[bij]N×M,其中 b i j = P ( x t = o j ∣ y t = s i ) , 1 ⩽ i ⩽ N , 1 ⩽ j ⩽ M {b_{ij}} = P\left( {{x_t} = {o_j}|{y_t} = {s_i}} \right),1 \leqslant i \leqslant N,1 \leqslant j \leqslant M bij=P(xt=oj∣yt=si),1⩽i⩽N,1⩽j⩽M表示任何时刻 t t t,若状态为 s i {{s_i}} si,则观测值 o j {{o_j}} oj被获取的概率。下文中下标 i j ij ij会视情况而灵活变化,当 i i i变为 y t y_t yt时,表示该时刻的状态变量 y t = s i y_t=s_i yt=si;当 j j j变为 x t x_t xt时,表示该时刻的状态变量 x t = s j x_t=s_j xt=sj。
在确定了状态空间 Y {\Bbb Y} Y、观测空间 X {\Bbb X} X和上述三组参数之后就确定了一个隐马尔可夫模型 λ = [ A , B , Π ] {\bf{\lambda }} = \left[ {{\bf{A}},{\bf{B}},\Pi } \right] λ=[A,B,Π],它按如下过程产生观测序列 { x 1 , x 2 , … , x T } \left\{ {{x_1},{x_2}, \ldots, {x_T}} \right\} {x1,x2,…,xT}:
1)设置 t = 1 t=1 t=1,根据初始状态概率 Π \Pi Π选择初始状态 y 1 y_1 y1;
2)根据状态 y t y_t yt和输出观测概率 B \bf{B} B选择观测变量取值 x t x_t xt;
3)根据状态 y t y_t yt和状态转移矩阵 A \bf{A} A转移模型状态,即确定 y t + 1 y_{t+1} yt+1;
4)若 t < T t<T t<T,设置 t = t + 1 t=t+1 t=t+1,并转到第2步,否则停止。
隐马尔可夫模型的三个基本问题:
1)给定模型 λ = [ A , B , Π ] {\bf{\lambda }} = \left[ {{\bf{A}},{\bf{B}},\Pi } \right] λ=[A,B,Π],如何计算观测序列 x = { x 1 , x 2 , ⋯ , x T } {\bf x}=\left\{ {{x_1},{x_2}, \cdots ,{x_T}} \right\} x={x1,x2,⋯,xT}的概率 P ( x ∣ λ ) P\left( {{\bf{x}}|{\bf{\lambda }}} \right) P(x∣λ),即如何评估模型与观测序列的匹配度?
2)给定模型 λ = [ A , B , Π ] {\bf{\lambda }} = \left[ {{\bf{A}},{\bf{B}},\Pi } \right] λ=[A,B,Π]和观测序列 x = { x 1 , x 2 , ⋯ , x T } x=\left\{ {{x_1},{x_2}, \cdots ,{x_T}} \right\} x={x1,x2,⋯,xT},如何找到与此观测序列最为匹配的状态序列 y = { y 1 , y 2 , ⋯ , y T } {\bf y}=\left\{ {{y_1},{y_2}, \cdots ,{y_T}} \right\} y={y1,y2,⋯,yT},即如何根据观测序列推断出隐藏的模型状态?
3)给定观测序列 x = { x 1 , x 2 , ⋯ , x T } {\bf x}=\left\{ {{x_1},{x_2}, \cdots, {x_T}} \right\} x={x1,x2,⋯,xT},如何调整模型参数 λ = [ A , B , Π ] {\bf{\lambda }} = \left[ {{\bf{A}},{\bf{B}},\Pi } \right] λ=[A,B,Π]使得该序列出现的概率 P ( x ∣ λ ) P\left( {{\bf{x}}|{\bf{\lambda }}} \right) P(x∣λ)最大,即如何训练模型?
概率计算算法
直接计算法
给定模型为 λ = [ A , B , Π ] {\bf{\lambda }} = \left[ {{\bf{A}},{\bf{B}},\Pi } \right] λ=[A,B,Π]和观测序列 x = { x 1 , x 2 , ⋯ , x T } {\bf x}=\left\{ {{x_1},{x_2}, \cdots, {x_T}} \right\} x={x1,x2,⋯,xT}。对于状态序列 y = { y 1 , y 2 , ⋯ , y T } {\bf y}=\left\{ {{y_1},{y_2}, \cdots ,{y_T}} \right\} y={y1,y2,⋯,yT},每个时刻的状态变量 y t y_t yt都有 { s 1 , s 2 , … , x N } \left\{ {{s_1},{s_2}, \ldots, {x_N}} \right\} {s1,s2,…,xN}N种可能,直接计算法就是列举所有的 y {\bf y} y序列(共 N T {N^T} NT种序列),然后对所有可能的状态序列求和,得到 P ( x ∣ λ ) P\left( {{\bf{x}}|{\bf{\lambda }}} \right) P(x∣λ)。
某一状态序列 y = { y 1 , y 2 , ⋯ , y T } {\bf y}=\left\{ {{y_1},{y_2}, \cdots ,{y_T}} \right\} y={y1,y2,⋯,yT}的概率是 P ( y ∣ λ ) = π y 1 a y 1 y 2 a y 2 y 3 ⋯ a y T − 1 y T P\left( {{\bf{y}}|{\bf{\lambda }}} \right) = {\pi _{{y_1}}}{a_{{y_1}{y_2}}}{a_{{y_2}{y_3}}} \cdots {a_{{y_{T - 1}}{y_T}}} P(y∣λ)=πy1ay1y2ay2y3⋯ayT−1yT,以此为前提的观测序列是 x = { x 1 , x 2 , ⋯ , x T } {\bf x}=\left\{ {{x_1},{x_2}, \cdots, {x_T}} \right\} x={x1,x2,⋯,xT}的概率是 P ( x ∣ y , λ ) = b y 1 x 1 b y 2 x 2 ⋯ b y T x T P\left( {{\bf{x|y,\lambda }}} \right) = {b_{{y_1}{x_1}}}{b_{{y_2}{x_2}}} \cdots {b_{{y_T}{x_T}}} P(x∣y,λ)=by1x1by2x2⋯byTxT, x {\bf{x}} x和 y {\bf{y}} y同时出现的联合概率为 P ( x , y ∣ λ ) = P ( x ∣ y , λ ) P ( y ∣ λ ) = π y 1 b y 1 x 1 a y 1 y 2 b y 2 x 2 ⋯ a y T − 1 y T b y T x T P\left( {{\bf{x,y}}|{\bf{\lambda }}} \right) = P\left( {{\bf{x}}|{\bf{y}},{\bf{\lambda }}} \right)P\left( {{\bf{y}}|{\bf{\lambda }}} \right) = {\pi _{{y_1}}}{b_{{y_1}{x_1}}}{a_{{y_1}{y_2}}}{b_{{y_2}{x_2}}} \cdots {a_{{y_{T - 1}}{y_T}}}{b_{{y_T}{x_T}}} P(x,y∣λ)=P(x∣y,λ)P(y∣λ)=πy1by1x1ay1y2by2x2⋯ayT−1yTbyTxT。对所有的状态序列 y {\bf y} y(共 N T {N^T} NT种序列)求和,得到观测序列 x {\bf x} x的概率 P ( x ∣ λ ) P\left( {{\bf{x}}|{\bf{\lambda }}} \right) P(x∣λ),即 P ( x ∣ λ ) = ∑ y P ( x ∣ y , λ ) P ( y ∣ λ ) = ∑ y 1 , y 2 , ⋯ , y T π y 1 b y 1 x 1 a y 1 y 2 b y 2 x 2 ⋯ a y T − 1 y T b y T x T P\left( {{\bf{x}}|{\bf{\lambda }}} \right) = \sum\limits_{\bf{y}} {P\left( {{\bf{x}}|{\bf{y}},{\bf{\lambda }}} \right)P\left( {{\bf{y}}|{\bf{\lambda }}} \right)} = \sum\limits_{{{\bf{y}}_{\bf{1}}}{\bf{,}}{{\bf{y}}_{\bf{2}}}{\bf{,}} \cdots {\bf{,}}{{\bf{y}}_{\bf{T}}}} {{\pi _{{y_1}}}{b_{{y_1}{x_1}}}{a_{{y_1}{y_2}}}{b_{{y_2}{x_2}}} \cdots {a_{{y_{T - 1}}{y_T}}}{b_{{y_T}{x_T}}}} P(x∣λ)=y∑P(x∣y,λ)P(y∣λ)=y1,y2,⋯,yT∑πy1by1x1ay1y2by2x2⋯ayT−1yTbyTxT直接法计算量极大,是 O ( T N T ) O\left( {T{N^T}} \right) O(TNT)阶的。有效算法:前向-后向算法。
前向算法
前向概率:给定隐马尔可夫模型 λ {\bf{\lambda }} λ,定义到时刻 t t t部分观测序列为 x 1 , x 2 , ⋯ , x t {x_1},{x_2}, \cdots ,{x_t} x1,x2,⋯,xt且状态为 s i {s_i} si的概率为前向概率,记作 α t ( i ) = P ( x 1 , x 2 , ⋯ , x t , y t = s i ∣ λ ) {\alpha _t}\left( i \right) = P\left( {{x_1},{x_2}, \cdots ,{x_t},{y_t} = {s_i}|{\bf{\lambda }}} \right) αt(i)=P(x1,x2,⋯,xt,yt=si∣λ)可以递推地前向概率 α t ( i ) {\alpha _t}\left( i \right) αt(i)及观测序列概率 P ( x ∣ λ ) P\left( {{\bf{x}}|{\bf{\lambda }}} \right) P(x∣λ)。
算法:
1)初值: α 1 ( i ) = π i b i x 1 , i = 1 , 2 , ⋯ , N {\alpha _1}\left( i \right) = {\pi _i}{b_{i{x_1}}},i = 1,2, \cdots ,N α1(i)=πibix1,i=1,2,⋯,N.
2)递推:对于 t = 1 , 2 , ⋯ , T − 1 t = 1,2, \cdots ,T - 1 t=1,2,⋯,T−1, α t + 1 ( i ) = [ ∑ j = 1 N α t ( j ) a j i ] b i x t + 1 , i = 1 , 2 , ⋯ , N {\alpha _{t + 1}}\left( i \right) = \left[ {\sum\limits_{j = 1}^N {{\alpha _{t}}\left( j \right){a_{ji}}} } \right]{b_{i{x_{t + 1}}}},i = 1,2, \cdots ,N αt+1(i)=[j=1∑Nαt(j)aji]bixt+1,i=1,2,⋯,N.
3)终止: P ( x ∣ λ ) = ∑ i = 1 N α T ( i ) P\left( {{\bf{x}}|{\bf{\lambda }}} \right) = \sum\limits_{i = 1}^N {{\alpha _T}\left( i \right)} P(x∣λ)=i=1∑NαT(i)
例:
考虑盒子和球模型 λ = ( A , B , π ) {\bf{\lambda }} = \left( {{\bf{A}},{\bf{B}},{\bf{\pi }}} \right) λ=(A,B,π),状态集合 S = { 1 , 2 , 3 } {S} = \left\{ {1,2,3} \right\} S={1,2,3},观测集合 O = { 红 , 白 } {O}= \left\{红 ,白 \right\} O={红,白}
A = [ 0.5 0.2 0.3 0.3 0.5 0.2 0.2 0.3 0.5 ] , B = [ 0.5 0.5 0.4 0.6 0.7 0.3 ] , Π = ( 0.2 , 0.4 , 0.4 ) T {\bf{A}}=\left[ \begin{matrix}0.5 & 0.2 & 0.3 \\0.3 & 0.5 & 0.2 \\0.2 & 0.3 & 0.5\end{matrix}\right],{\bf{B}}=\left[ \begin{matrix}0.5 & 0.5 \\0.4 & 0.6 \\0.7 & 0.3 \end{matrix}\right],\Pi={\left( {0.2,0.4,0.4} \right)^T} A=⎣⎡0.50.30.20.20.50.30.30.20.5⎦⎤,B=⎣⎡0.50.40.70.50.60.3⎦⎤,Π=(0.2,0.4,0.4)T设 T = 3 T=3 T=3,观测序列 x = { 红 , 白 , 红 } {\bf{x}} = \left\{ {红,白,红} \right\} x={红,白,红}。
s 1 s 2 s 3 s 1 0.5 0.2 0.3 s 2 0.3 0.5 0.2 s 3 0.2 0.3 0.5 o 1 o 2 s 1 0.5 0.5 s 2 0.4 0.6 s 3 0.7 0.3 \begin{matrix}&{s_1}&{s_2}&{s_3}\\{s_1}&0.5 & 0.2 & 0.3 \\{s_2}&0.3 & 0.5 & 0.2 \\{s_3}&0.2 & 0.3 & 0.5\end{matrix}\qquad \begin{matrix}&{o_1}&{o_2}&\\{s_1}&0.5 & 0.5 \\{s_2}&0.4 & 0.6 \\{s_3}&0.7 & 0.3 \end{matrix} s1s2s3s10.50.30.2s20.20.50.3s30.30.20.5s1s2s3o10.50.40.7o20.50.60.3
1)计算初值( t = 1 t=1 t=1)
α 1 ( 1 ) = π 1 b 1 x 1 = 0.2 × 0.5 = 0.10 {\alpha _1}\left( 1 \right) = {\pi _1}{b_{1{x_1}}} = 0.2 \times 0.5 = 0.10 α1(1)=π1b1x1=0.2×0.5=0.10 α 1 ( 2 ) = π 2 b 2 x 1 = 0.4 × 0.4 = 0.16 {\alpha _1}\left( 2 \right) = {\pi _2}{b_{2{x_1}}} = 0.4 \times 0.4 = 0.16 α1(2)=π2b2x1=0.4×0.4=0.16 α 1 ( 3 ) = π 3 b 3 x 1 = 0.4 × 0.7 = 0.28 {\alpha _1}\left( 3 \right) = {\pi _3}{b_{3{x_1}}} = 0.4 \times 0.7 = 0.28 α1(3)=π3b3x1=0.4×0.7=0.28
2)递推计算
t = 2 : t=2: t=2:
α 2 ( 1 ) = [ ∑ i = 1 3 α 1 ( i ) a i 1 ] b 1 x 2 = ( 0.10 × 0.5 + 0.16 × 0.3 + 0.28 × 0.2 ) × 0.5 = 0.077 {\alpha _2}\left( 1 \right) = \left[ {\sum\limits_{i = 1}^3 {{\alpha _1}\left( i \right){a_{i1}}} } \right]{b_{1{x_2}}} = \left( {0.10 \times 0.5 + 0.16 \times 0.3 + 0.28 \times 0.2} \right) \times 0.5 = 0.077 α2(1)=[i=1∑3α1(i)ai1]b1x2=(0.10×0.5+0.16×0.3+0.28×0.2)×0.5=0.077 α 2 ( 2 ) = [ ∑ i = 1 3 α 1 ( i ) a i 2 ] b 2 x 2 = ( 0.10 × 0.2 + 0.16 × 0.5 + 0.28 × 0.3 ) × 0.6 = 0.1104 {\alpha _2}\left( 2 \right) = \left[ {\sum\limits_{i = 1}^3 {{\alpha _1}\left( i \right){a_{i2}}} } \right]{b_{2{x_2}}} = \left( {0.10 \times 0.2 + 0.16 \times 0.5 + 0.28 \times 0.3} \right) \times 0.6 = 0.1104 α2(2)=[i=1∑3α1(i)ai2]b2x2=(0.10×0.2+0.16×0.5+0.28×0.3)×0.6=0.1104 α 2 ( 3 ) = [ ∑ i = 1 3 α 1 ( i ) a i 3 ] b 3 x 2 = ( 0.10 × 0.3 + 0.16 × 0.2 + 0.28 × 0.5 ) × 0.3 = 0.0606 {\alpha _2}\left( 3 \right) = \left[ {\sum\limits_{i = 1}^3 {{\alpha _1}\left( i \right){a_{i3}}} } \right]{b_{3{x_2}}} = \left( {0.10 \times 0.3 + 0.16 \times 0.2 + 0.28 \times 0.5} \right) \times 0.3 = 0.0606 α2(3)=[i=1∑3α1(i)ai3]b3x2=(0.10×0.3+0.16×0.2+0.28×0.5)×0.3=0.0606
t = 3 : t=3: t=3:
α 3 ( 1 ) = [ ∑ i = 1 3 α 2 ( i ) a i 1 ] b 1 x 3 = ( 0.077 × 0.5 + 0.1104 × 0.3 + 0.0606 × 0.2 ) × 0.5 = 0.04187 {\alpha _3}\left( 1 \right) = \left[ {\sum\limits_{i = 1}^3 {{\alpha _2}\left( i \right){a_{i1}}} } \right]{b_{1{x_3}}} = \left( {0.077 \times 0.5 + 0.1104 \times 0.3 + 0.0606 \times 0.2} \right) \times 0.5 = 0.04187 α3(1)=[i=1∑3α2(i)ai1]b1x3=(0.077×0.5+0.1104×0.3+0.0606×0.2)×0.5=0.04187 α 3 ( 2 ) = [ ∑ i = 1 3 α 2 ( i ) a i 2 ] b 2 x 3 = ( 0.077 × 0.2 + 0.1104 × 0.5 + 0.0606 × 0.3 ) × 0.4 = 0.035512 {\alpha _3}\left( 2 \right) = \left[ {\sum\limits_{i = 1}^3 {{\alpha _2}\left( i \right){a_{i2}}} } \right]{b_{2{x_3}}} = \left( {0.077 \times 0.2 + 0.1104 \times 0.5 + 0.0606 \times 0.3} \right) \times 0.4 = 0.035512 α3(2)=[i=1∑3α2(i)ai2]b2x3=(0.077×0.2+0.1104×0.5+0.0606×0.3)×0.4=0.035512 α 3 ( 3 ) = [ ∑ i = 3 3 α 2 ( i ) a i 3 ] b 3 x 3 = ( 0.077 × 0.3 + 0.1104 × 0.2 + 0.0606 × 0.5 ) × 0.5 = 0.052836 {\alpha _3}\left( 3 \right) = \left[ {\sum\limits_{i = 3}^3 {{\alpha _2}\left( i \right){a_{i3}}} } \right]{b_{3{x_3}}} = \left( {0.077 \times 0.3 + 0.1104 \times 0.2 + 0.0606 \times 0.5} \right) \times 0.5 = 0.052836 α3(3)=[i=3∑3α2(i)ai3]b3x3=(0.077×0.3+0.1104×0.2+0.0606×0.5)×0.5=0.052836
3)终止 P ( x ∣ λ ) = ∑ i = 1 3 α 3 ( i ) = 0.04187 + 0.35512 + 0.052836 = 0.130218 P\left( {{\bf{x}}|{\bf{\lambda }}} \right) = \sum\limits_{i = 1}^3 {{\alpha _3}\left( i \right) = 0.04187 + 0.35512 + 0.052836 = 0.130218} P(x∣λ)=i=1∑3α3(i)=0.04187+0.35512+0.052836=0.130218
这一部分的Java实现。
后向算法
后向概率:给定隐马尔可夫模型 λ {\bf{\lambda }} λ,定义到时刻 t t t状态变量为 s i {s_i} si的条件下,从 t + 1 t+1 t+1到 T T T的观测序列为 x t + 1 , x t + 2 , ⋯ x T {x_{t + 1}},{x_{t + 2}}, \cdots {x_T} xt+1,xt+2,⋯xT的概率为后向概率,记作 β t ( i ) = P ( x t + 1 , x t + 2 , ⋯ , x T ∣ y t = s i , λ ) {\beta _t}\left( i \right) = P\left( {{x_{t + 1}},{x_{t + 2}}, \cdots, {x_T}|{y_t} = {s_i},{\bf{\lambda }}} \right) βt(i)=P(xt+1,xt+2,⋯,xT∣yt=si,λ)可以递推后向概率 β t {\beta _t} βt及观测序列概率 P ( x ∣ λ ) P\left( {{\bf{x}}|{\bf{\lambda }}} \right) P(x∣λ)。
1)初值: β T ( i ) = 1 , i = 1 , 2 , ⋯ , N {\beta _T}\left( i \right) = 1,i = 1,2, \cdots ,N βT(i)=1,i=1,2,⋯,N
2)递推:对 t = T − 1 , T − 2 , ⋯ , 1 t = T - 1,T - 2, \cdots ,1 t=T−1,T−2,⋯,1 β t ( i ) = ∑ j = 1 N a i j b j x t + 1 β t + 1 ( j ) , i = 1 , 2 , ⋯ , N {\beta _t}\left( i \right) = \sum\limits_{j = 1}^N {{a_{ij}}{b_{j{x_{t + 1}}}}{\beta _{t + 1}\left( j \right)},i = 1,2, \cdots ,N} βt(i)=j=1∑Naijbjxt+1βt+1(j),i=1,2,⋯,N
3)终止: P ( x ∣ λ ) = ∑ i = 1 N π i b i x 1 β 1 ( i ) P\left( {{\bf{x}}|{\bf{\lambda }}} \right) = \sum\limits_{i = 1}^N {{\pi _i}{b_{i{x_1}}}{\beta _1}\left( i \right)} P(x∣λ)=i=1∑Nπibix1β1(i)
例:
模型同上。
1)计算初值( t = 3 t=3 t=3) β 3 ( 1 ) = 1 , β 3 ( 2 ) = 1 , β 3 ( 3 ) = 1 {\beta _3}\left( 1 \right) = 1,{\beta _3}\left( 2 \right) = 1,{\beta _3}\left( 3 \right) = 1 β3(1)=1,β3(2)=1,β3(3)=1
2)递推计算
t = 2 : t=2: t=2: β 2 ( 1 ) = ∑ j = 1 3 a 1 j b j x 3 β 3 ( j ) = 0.5 × 0.5 × 1 + 0.2 × 0.4 × 1 + 0.3 × 0.7 × 1 = 0.54 {\beta _2}\left( 1 \right) = \sum\limits_{j = 1}^3 {{a_{1j}}{b_{j{x_3}}}{\beta _3}\left( j \right)} = 0.5 \times 0.5 \times 1 + 0.2 \times 0.4 \times 1 + 0.3 \times 0.7 \times 1 = 0.54 β2(1)=j=1∑3a1jbjx3β3(j)=0.5×0.5×1+0.2×0.4×1+0.3×0.7×1=0.54 β 2 ( 2 ) = ∑ j = 1 3 a 2 j b j x 3 β 3 ( j ) = 0.3 × 0.5 × 1 + 0.5 × 0.4 × 1 + 0.2 × 0.7 × 1 = 0.49 {\beta _2}\left( 2 \right) = \sum\limits_{j = 1}^3 {{a_{2j}}{b_{j{x_3}}}{\beta _3}\left( j \right)} = 0.3 \times 0.5 \times 1 + 0.5 \times 0.4 \times 1 + 0.2 \times 0.7 \times 1 = 0.49 β2(2)=j=1∑3a2jbjx3β3(j)=0.3×0.5×1+0.5×0.4×1+0.2×0.7×1=0.49 β 2 ( 3 ) = ∑ j = 1 3 a 3 j b j x 3 β 3 ( j ) = 0.2 × 0.5 × 1 + 0.3 × 0.4 × 1 + 0.5 × 0.7 × 1 = 0.57 {\beta _2}\left( 3 \right) = \sum\limits_{j = 1}^3 {{a_{3j}}{b_{j{x_3}}}{\beta _3}\left( j \right)} = 0.2 \times 0.5 \times 1 + 0.3 \times 0.4 \times 1 + 0.5 \times 0.7 \times 1 = 0.57 β2(3)=j=1∑3a3jbjx3β3(j)=0.2×0.5×1+0.3×0.4×1+0.5×0.7×1=0.57
t = 1 : t=1: t=1: β 1 ( 1 ) = ∑ j = 1 3 a 1 j b j x 2 β 2 ( j ) = 0.5 × 0.5 × 0.54 + 0.2 × 0.6 × 0.49 + 0.3 × 0.3 × 0.57 = 0.2451 {\beta _1}\left( 1 \right) = \sum\limits_{j = 1}^3 {{a_{1j}}{b_{j{x_2}}}{\beta _2}\left( j \right)} = 0.5 \times 0.5 \times 0.54 + 0.2 \times 0.6 \times 0.49 + 0.3 \times 0.3 \times 0.57 = 0.2451 β1(1)=j=1∑3a1jbjx2β2(j)=0.5×0.5×0.54+0.2×0.6×0.49+0.3×0.3×0.57=0.2451 β 1 ( 2 ) = ∑ j = 1 3 a 2 j b j x 2 β 2 ( j ) = 0.3 × 0.5 × 0.54 + 0.5 × 0.6 × 0.49 + 0.2 × 0.3 × 0.57 = 0.2622 {\beta _1}\left( 2 \right) = \sum\limits_{j = 1}^3 {{a_{2j}}{b_{j{x_2}}}{\beta _2}\left( j \right)} = 0.3 \times 0.5 \times 0.54 + 0.5 \times 0.6 \times 0.49 + 0.2 \times 0.3 \times 0.57 = 0.2622 β1(2)=j=1∑3a2jbjx2β2(j)=0.3×0.5×0.54+0.5×0.6×0.49+0.2×0.3×0.57=0.2622 β 1 ( 3 ) = ∑ j = 1 3 a 3 j b j x 2 β 2 ( j ) = 0.2 × 0.5 × 0.54 + 0.3 × 0.6 × 0.49 + 0.5 × 0.3 × 0.57 = 0.2277 {\beta _1}\left( 3 \right) = \sum\limits_{j = 1}^3 {{a_{3j}}{b_{j{x_2}}}{\beta _2}\left( j \right)} = 0.2 \times 0.5 \times 0.54 + 0.3 \times 0.6 \times 0.49 + 0.5 \times 0.3 \times 0.57 = 0.2277 β1(3)=j=1∑3a3jbjx2β2(j)=0.2×0.5×0.54+0.3×0.6×0.49+0.5×0.3×0.57=0.2277
3)终止 P ( x ∣ λ ) = 0.2 × 0.5 × 0.2451 + 0.4 × 0.4 × 0.2622 + 0.4 × 0.7 × 0.2277 = 0.130218 P\left( {{\bf{x}}|{\bf{\lambda }}} \right) = 0.2 \times 0.5 \times 0.2451 + 0.4 \times 0.4 \times 0.2622 + 0.4 \times 0.7 \times 0.2277 = 0.130218 P(x∣λ)=0.2×0.5×0.2451+0.4×0.4×0.2622+0.4×0.7×0.2277=0.130218
前向算法和后向算法的计算量都是 O ( N 2 T ) O\left( {{N^2}T} \right) O(N2T)阶的,可以将前向算法和后向算法统一写成 P ( x ∣ λ ) = ∑ i = 1 N ∑ j = 1 N α t ( i ) a i j b j x t + 1 β t + 1 ( j ) , t = 1 , 2 , ⋯ , T − 1 P\left( {x|\lambda } \right) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _t}\left( i \right){a_{ij}}{b_{j{x_{t + 1}}}}{\beta _{t + 1}}\left( j \right)} ,t = 1,2, \cdots ,T - 1} P(x∣λ)=i=1∑Nj=1∑Nαt(i)aijbjxt+1βt+1(j),t=1,2,⋯,T−1
这一部分的Java实现。
一些概率与期望值的计算
1.给定模型 λ \lambda λ和观测 x {\bf{x}} x,在时刻 t t t处于状态 s i s_i si的概率,记 γ t ( i ) = P ( y t = s i ∣ x , λ ) {\gamma _t}\left( i \right) = P\left( {{y_t} = {s_i}|{\bf{x,\lambda }}} \right) γt(i)=P(yt=si∣x,λ)。
由前后向概率,有 α t ( i ) β t ( i ) = P ( y t = s i , x ∣ λ ) {\alpha _t}\left( i \right){\beta _t}\left( i \right) = P\left( {{y_t} = {s_i},{\bf{x}}|{\bf{\lambda }}} \right) αt(i)βt(i)=P(yt=si,x∣λ)。于是有: γ t ( i ) = P ( y t = s i ∣ x , λ ) = P ( y t = s i , x ∣ λ ) P ( x ∣ λ ) = α t ( i ) β t ( i ) ∑ j = 1 N α t ( j ) β t ( j ) {\gamma _t}\left( i \right) = P\left( {{y_t} = {s_i}|{\bf{x,\lambda }}} \right) = \frac{{P\left( {{y_t} = {s_i},{\bf{x}}|{\bf{\lambda }}} \right)}}{{P\left( {{\bf{x}}|{\bf{\lambda }}} \right)}} = \frac{{{\alpha _t}\left( i \right){\beta _t}\left( i \right)}}{{\sum\limits_{j = 1}^N {{\alpha _t}\left( j \right){\beta _t}\left( j \right)} }} γt(i)=P(yt=si∣x,λ)=P(x∣λ)P(yt=si,x∣λ)=j=1∑Nαt(j)βt(j)αt(i)βt(i)
2.给定模型 λ \lambda λ和观测 x {\bf{x}} x,在时刻 t t t处于状态 s i s_i si且在时刻 t + 1 t+1 t+1处于状态 s j s_j sj的概率,记 ξ t ( i , j ) = P ( y t = s i , y t + 1 = s j ∣ x , λ ) {\xi _t}\left( {i,j} \right) = P\left( {{y_t} = {s_i},{y_{t + 1}} = {s_j}|{\bf{x}},{\bf{\lambda }}} \right) ξt(i,j)=P(yt=si,yt+1=sj∣x,λ)。由前后向概率,有 α t ( i ) a i j b j x t + 1 β t + 1 ( j ) = P ( y t = s i , y t + 1 = s j ∣ x , λ ) {\alpha _t}\left( i \right){a_{ij}}{b_{j{x_{t + 1}}}}{\beta _{t + 1}}\left( j \right) = P\left( {{y_t} = {s_i},{y_{t + 1}} = {s_j}|{\bf{x}},{\bf{\lambda }}} \right) αt(i)aijbjxt+1βt+1(j)=P(yt=si,yt+1=sj∣x,λ)。于是有 ξ t ( i , j ) = P ( y t = s i , y t + 1 = s j , x ∣ λ ) P ( x ∣ λ ) = α t ( i ) a i j b j x t + 1 β t + 1 ( j ) ∑ i = 1 N ∑ j = 1 N α t ( i ) a i j b j x t + 1 β t + 1 ( j ) {\xi _t}\left( {i,j} \right) = \frac{{P\left( {{y_t} = {s_i},{y_{t + 1}} = {s_j},{\bf{x}}|{\bf{\lambda }}} \right)}}{{P\left( {{\bf{x}}|{\bf{\lambda }}} \right)}} = \frac{{{\alpha _t}\left( i \right){a_{ij}}{b_{j{x_{t + 1}}}}{\beta _{t + 1}}\left( j \right)}}{{\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _t}\left( i \right){a_{ij}}{b_{j{x_{t + 1}}}}{\beta _{t + 1}}\left( j \right)} } }} ξt(i,j)=P(x∣λ)P(yt=si,yt+1=sj,x∣λ)=i=1∑Nj=1∑Nαt(i)aijbjxt+1βt+1(j)αt(i)aijbjxt+1βt+1(j)
3.将 γ t ( i ) {\gamma _t}\left( i \right) γt(i)和 ξ t ( i , j ) {\xi _t}\left( {i,j} \right) ξt(i,j)对各个时刻 t t t求和,可以得到一些有用的期望值:
1)在观测 x {\bf{x}} x下状态 s i s_i si出现的期望值为 ∑ t = 1 T γ t ( i ) \sum\limits_{t = 1}^T {{\gamma _t}\left( i \right)} t=1∑Tγt(i)。
2)在观测 x {\bf{x}} x下由状态 s i s_i si转移的期望值为 ∑ t = 1 T γ t ( i ) \sum\limits_{t = 1}^T {{\gamma _t}\left( i \right)} t=1∑Tγt(i)。
3)在观测 x {\bf{x}} x下由状态 s i s_i si转移到状态 s j s_j sj的期望值 ∑ t = 1 T ξ t ( i , j ) \sum\limits_{t = 1}^T {{\xi _t}\left( {i,j} \right)} t=1∑Tξt(i,j)。
这些将在HMM的训练中被用到。
下一篇《EM算法》