分布式图并行计算框架：PowerGraph

1. About Joseph E.Conzalez

首先关于约瑟夫，他目前在伯克利AMP实验室做博士后，这是他博客的一个截图。在他博客中写道，下个月即2016年1月份将要当任伯克利的助理教授。

在看了他的简历后，发现他居然也是Spark Graphx的第一作者，并且Graphx这篇论论文也是发表在OSDI上，非常牛逼！戳这里，是他的博客地址。

---

2. About OSDI

第二个要介绍的是关于OSDI这个会议，PowerGraph这篇文章是发表在2012年OSDI会议上，OSDI，它的全称是Operating Systems Design and Implementation。

它与另一个会议SOSP被公认为是System方面最好的会议，每两年开一次，轮流开，比如今年是SOSP，明年就是OSDI，一般是偶数年是OSDI。发表在上面的文章数，以前维持在每届20篇左右，从2002年开始稳定在每届27篇

下面这张表列出了目前有哪些科研机构和学校在OSDI上发表过文章，以及总共发表文章的数目是多少。可以看出这里都是世界顶尖级别的理工学校，像MIT（麻省理工），Princeton，Standford，Berkeley，CMU。

机构	文章数目
MIT	14
Microsoft	13
Princeton	12
Washington	12
Stanford	11
Berkeley	10
CMU	10
Michigan	7
Arizona	6
Rice	6

OSDI已经是计算机学界最顶级会议之一，很多革命性成果都在这里发表，比如MapReduce和BigTable等等。刚才提到本文作者Joseph已经以第一作者的身份在OSDI上发表了两篇文章。据统计目前国内只有2人中过该会，一个是清华牟帅在国外交流访问期间中过一篇，百度少帅李沐在CMU期间中过一篇。

这里在给大家科普一下usenix，USENIX成立于1975年，当时的名字叫做”Unix用户群”。它的主要目的是学习及开发Unix以及类似系统。1977年六月，美国电话电报公司的律师告诉用户群他们不能继续使用UNIX这个名字，因为UNIX是美国电话电报公司所拥有的一个商标。所以这个用户群更名成USENIX.从那以后，USENIX逐渐发展成一个倍受尊敬的由计算机操作系统用户，开发者和研究者所组成的机构。USENIX每年赞助好几个学术会议和工作室会议，其中最有名的是OSDI。

---

3. PowerGraph && GraphLab

第三个这里要介绍下，PowerGraph和GraphLab 是什么关系。

之前我在接触图计算时，只知道有GraphLab。其实平时我们狭义上说的GraphLab图计算指的就是PowerGraph，而PowerGraph后来被集成到GraphLab后只是GraphLab一个主要的底层框架，GraphLab实际上是一个机器学习框架，里面实现了非常多的机器学习算法，之前GraphLab是一个开源项目，但它在接受了两轮投资之后已经由原来的免费项目变成了一个付费试用的项目。网址由原来的graphlab.org也变成了dato.com。

上面这个是GraphLab的Logo，官网首页中用这样一句话来形容GraphLab，让复杂的机器学习就和写Hello World一样简单。GraphLab快得益于PowerGraph设计

业界对PowerGraph认可度是非常高的，称它能轻松搞定TB级数据，计算能力突破人类图计算“极限值”。

下面将正式论述该论文。

---

4. Graphs are ubiquitous

我们都知道，图在我们生活中是无所不在的。

社交媒体、科学中分子结构关系、电商平台的广告推荐、网页信息

图是能够将人、产品、想法、事实、兴趣爱好之间的关系进行编码，转成一种结构进行存储。

图的一个特点是：Big，数十亿的点和边以及丰富的元数据。

各种场景下的信息都能转成图来表示，同时我们可以利用图来进行数据挖掘和机器学习，比如
识别出有影响力的人和信息、社区发现、寻找产品和广告的投放用户、给有依赖关系的复杂数据构建模型等等这些都可以使用图来完成

下面要介绍论文中的第一个概念 ：Natural Graphs
从不同平台或实际应用中产生的图我们称为：Natural Graphs

面对各种应用中如此海量的Natural Graphs，现有分布式的图处理平台处理性能还是比较低效的。

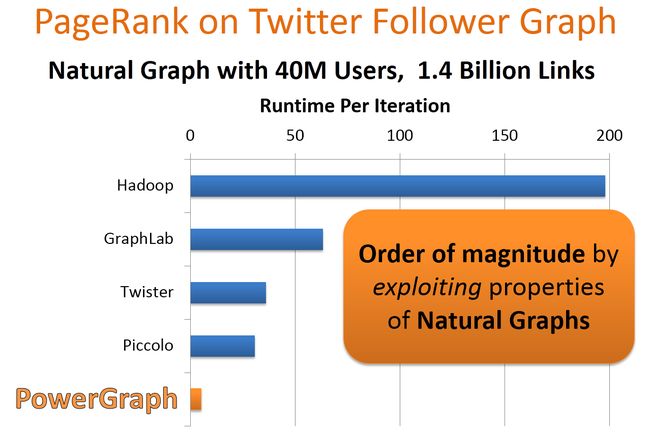
作者选用Twitter数据集测试目前几个主流分布式平台在处理这种Natural Graph的性能，这里是利用PageRank算法每次迭代的时间作为横轴，纵坐标是不同的分布式平台，可以看到Hadoop和原生态的GraphLab的处理时间还是很长的，性能最好的是Piccolo，它是Google的Pregel的C++实现 。

而PowerGraph的处理时间更短，达到了数量级的性能提升。

---

5. Power-Law Degree Distribution

下面我们来看一下，Natural Graph这种图到底有什么特点，为什么大部分分布式处理系统性能都比较低效，PowerGraph在Natural Graph有如此好的性能。Natural Graphs的属性特点是满足密率度分布。

下面我们来看下什么叫密率度分布。

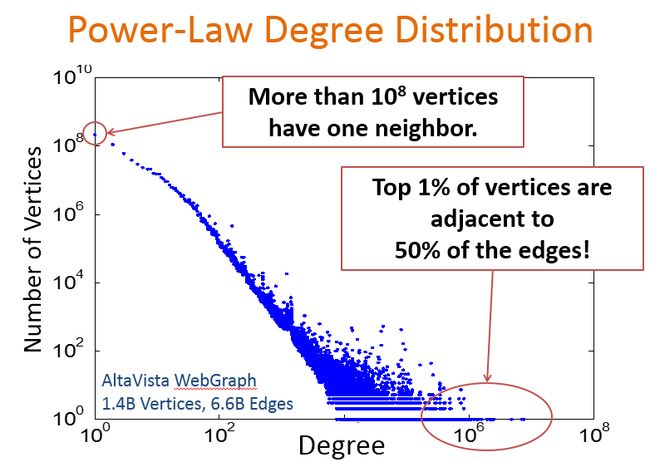
简单来说，幂律有两个通俗的解释，一个是“长尾”理论，只有少数明星是有很多人关注的，但是还有大部分人只有少部分人关注。长尾理论就是对幂律通俗化的解释。

另外一个通俗解释就是马太效应，穷者越穷富者越富。

从这幅图可以看出，只有一个邻居的点的数目有超过10的8次方个，而仅有那1%的点却占了整个图50%的边。这些点被称为高纬度点。

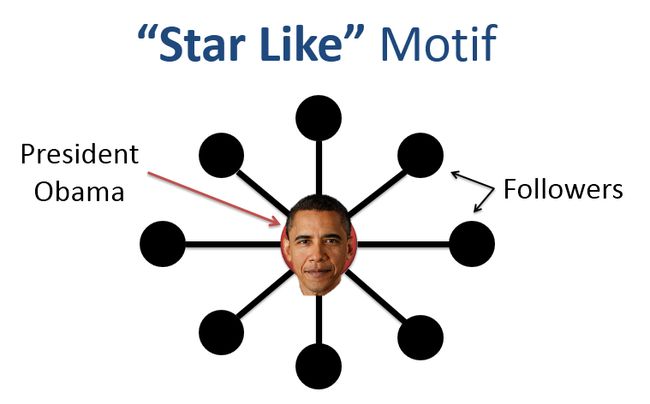
这里举一个明星效应的例子，比如这里表示社交网络中的一个子图，中间红色点表示某个用户，旁边黑点表示的是所有的粉丝，比如这里我们一个黑点表示100w的用户，那么这个人可能就是obama，但像obama这样拥有这么多粉丝的人是非常少的，大部分人粉丝只有大黑点中的一个点，几百或者多者上千。这就是我们说的密率度分布图的特点。

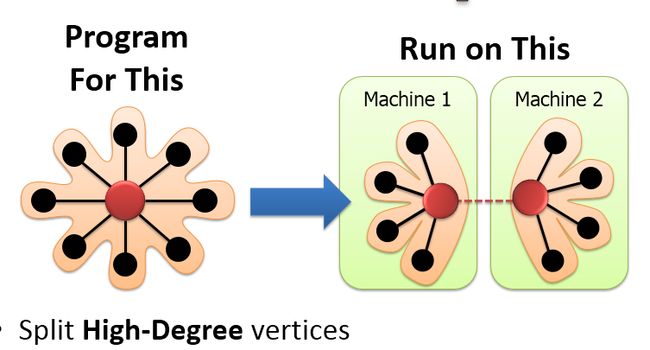
PowerGraph中在计算时会切分高纬度点，被切分的点形成了一个新的抽象。

但是在节点切分策略下要解决的一个问题是如何运行节点程序？在之前的边切分策略下节点是单一的、完整的，节点拥有所有邻居的信息，可以独立完成节点程序的运算。但是在节点切分策略下，每个节点看到的只是部分的邻居，无法完成整个计算。

在节点切分策略下，分布在不同的CPU或者机器上的节点如何对其进行编程？

下面将介绍两种目前最具代表性的图计算方法是如何对图进行并行化抽象计算的。

图并行化抽象目前流行的两种方法是
——使用消息 Pregel
——共享状态 GraphLab

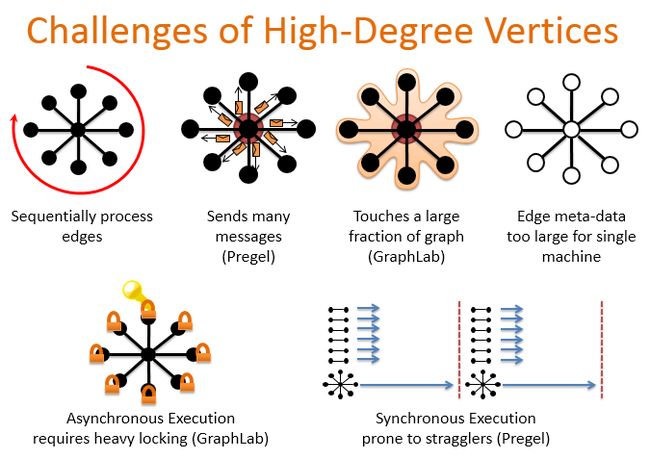
但对于我们前面提到的密率图，Pregel和GraphLab都不能很好地处理这种节点。最大的挑战就是如何来处理这些高维度的点。

最简单也最低效的方法是序列化处理这些边，说白了就是遍历所有点。

第二种方法就是刚才提到的Pregel，它处理高纬度点的缺陷是单个worker要发送大量消息给邻居节点，

GraphLab的方法的缺点是会触到图的大部分（GraphLab）

并且对于单台机器边的元数据太大

GraphLab共享状态是异步执行，需要大量锁
Pregel同步执行但容易产生straggler，straggler可以理解为执行比较慢的节点。木桶的短板效应

导致这些系统中存在这些问题主要原因是他们对图的切分策略是采用边分割的方式。

---

6. Edge-Cut and Vertex-Cut

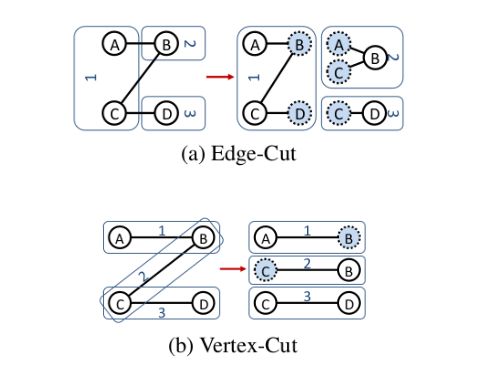
还有一种是点切分的方式，下面我们看下边切分的方式和点切分方式有什么不同，
我们现在要将一个有4个顶点的图存储到3台机器上，这三台机器分别叫1，2，3。那么按照边切分的方式，这且边被切人后在3台机器的分布如右边图。
从图中可以看出，切分的过程中，总共有AB,BC,CD三条边被切开，保存到3台机器后，边的总数目由原来的3条，变成了6条，多了一倍，外加5个节点副本。

第二种方式是点切分方式，同样是4个节点的图，我们将B、C节点切分开来。存储到3台机器后，得到右边这个图，可以看出我们的边的数目还是3台，只多了两个节点的副本。

所以当边的数量比节点数量大很多的情况下，这种两种切分方式差异会更加明显。

图的切分问题又叫着图分区。图并行抽象的性能要依赖于图的分区方式，
而我们的目标是
——最小化通信
——权衡图计算和存储开销

而前面提到的两种流行的图处理框架GraphLab和Pregel采用的都是边切分方式的随机Hash分区策略这种策略只保证了节点均匀分布在整个集群中，边被切分成双份分散在整个集群中。

对于一般图来说，边的数量是要远大于点的数量，因此按边分区会带来存储和计算上的不均衡。

论文中总结了这种边切分方式带来的影响，给出了一个公式用来求被切的边除以总的边的均值，p表示随机被分的机器数目，当p等于10时有90%的边被切分，当p等于100时，有99%的边会被切。

可以看出，当我们集群规模越大，按照边来切分方式进行分区是非常划不来的，图中大部分边会变切分开来。

---

7. PowerGraph

这里总结一下目前对于专门的图处理框架GraphLab和Pregel是不适合处理这种natural graphs
主要的两大挑战是高纬度的点和低质量的分区策略。

本文提出的PowerGraph即是为了解决这2个问题而设计的，其中Power的意思就是密分布的意思。

下面就来介绍PowerGraph的详细设计细节：

PowerGraph的主要贡献或者说创新点可归结为以下两点：

第一，提出了GAS计算模型，将高维度的点进行并行化

第二是采用点切分策略，来保证整个集群的均衡性，该策略对大量密率图分区是非常高效的。

---

8. GAS Decomposition

下面以PageRank为例，顶点程序的通用模板大致如图所示，第一步收集邻居节点信息，第二步更新节点权值，如果还没有收敛，触发节点邻居再次运行顶点程序。
这是一种通用的处理模板

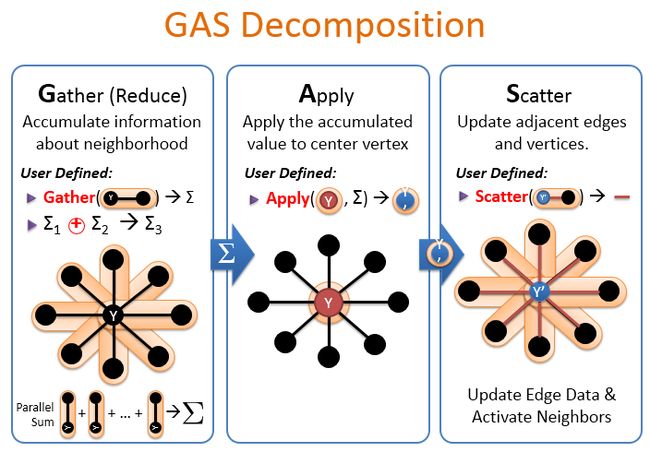
PowerGraph提出了自己的一套计算模型，叫GAS分解。G是Gather的意思，A是Apply的意思，S是Scatter的意思。

GAS分解过程如下，

Gather：收集邻居信息
先收集同一台机器的信息，然后对不同主机收集的信息进行汇总。得到最后的求和信息。

Apply：对中心点应用收集点的值，得到y一撇

Scatter（分散）：更新邻居点和边，触发邻居点进行下一轮迭代。

那么就PowerGraph的GAP模型应用到RageRank算法中，是什么样的过程？

该公式中i表示目标节点，我们需要对这个节点求PageRank值，wij表示从j点到i点的权值，

Gather阶段，先求i所有邻居节点的权值，用户自定义一个sum操作，统计所有邻居节点的权值之和。

Apply阶段更新i点的权值，利用上一阶段的sum值加上一个偏置值，计算得到i的新的权值；

Scatter阶段如果i值被修改，就触发相应的邻居节点j重新计算。

下面用一个动画演示PowerGraph是如何执行顶点程序。

当顶点按点切分方式被分到4台机器之后，在多个节点上指派一个为Master,其余的为Mirror。

Mirror上可以运行Gather程序来收集所有邻居的信息，并进行聚合计算(sum)后发送给Master。

Master上的Gather程序收集这些结果，最终将这个结果应用到Apply程序上，得到新的节点状态。然后通过Scatter程序将新的节点状态广播给各个Mirror，Mirror进而广播给各个邻居。

---

9. Constructing Vertex-Cuts

PowerGraph提出了一种均衡图划分方案，在减少计算中通信量的同时保证负载均衡。

实际上通信开销是和节点所跨的机器数目成线性关系，但点切分的方式可以最小化每个顶点所跨的机器数目。

PowerGraph使用的不是边切分，边切分前面已经提到会同步大量的边的信息。

而是采用点切分，点切分只要同步一个点的节点信息。

论文中给出了一个新的理论（定理）：对于任何边切分我们都可以直接构造一个点切分，能够严格减少通信和存储开销。下面将介绍该论文是如何来构造这个点分割。

论文提出了3种分配方式
随机边分配
贪婪协同边分配
非贪婪边分配（Oblivious遗忘）

第一种策略是随机的边放置策略，按照点切分的方式，随机放置边

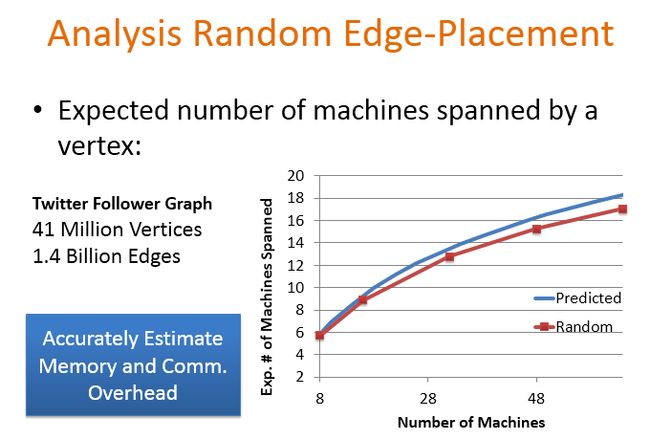
下面分析边这种随机边放置策略的性能

这里数据集选用的是Twitter数据集，有410w个顶点，14亿条边 。横坐标是实际集群中机器的数目，纵坐标表示1个顶点期望跨了机器数目，关于这两者的数量关系公式，作者在论文中给出了一个定理。蓝色的线表示表示理论推测期望值，红线是实际随机边放置的曲线图。可以看出期望值和理论值之间基本是能够match上的。所以针对随即边放置策略，就可以做到精确的估计内存和通信开销。

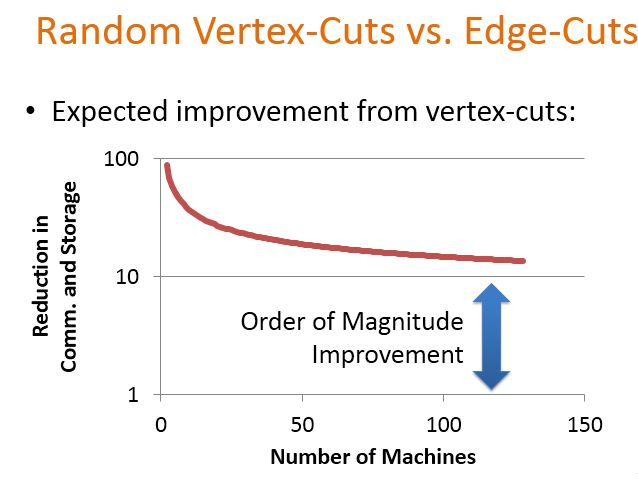
下面给出了点切分策略相对于边切分策略性能上的提升，横坐标还是机器数目，纵坐标是点切分相对于边切分在通信和存储开销上减少的幅度，当机器数目比较少时，减少了接近100倍，随着机器数目增大，通信和存储开销减少了大概10倍左右，即点切分的性能相对于边切分提升了将近10倍。



第二种是贪婪的点切分方式，由于随机切分下，尽管各个子图基本均衡，但是子图内部联通性很差。因此PowerGraph提出的启发式的贪婪算法，基本原理如下：
如果新加进来的边，它的某个节点已经存在于某台机器上，就将该边分到对应的机器上，比如在1号机器上已经存在AB这条边，2号机器上已经存在BC这条边，那门当一条新的边AD在要加进来时，发现A节点已经在1号机器上，所以就将该边放置到1号机器上。如果再来一条边BE，发向两台机器上都存有B节点，这时候贪婪策略会选择机器中分配的边最少的机器进行分配。所以会将BE分配到2号机器，这里只是简单的举了个例子，论文中是用集合的表示方式将这种贪婪策略归纳了4种case，这里不详细介绍，具体可以参考论文第8页相关内容。

上面提到的贪婪策略，作者论文中称之为De-randomiztion。de的含义这里因该是去除，与随机化刚好是反义词。De-randomization就是Greedy的含义，贪婪点切分能够最小化机器所跨的机器数目。实际的贪婪的放置策略性能要比随即放置策略要好。关于贪婪边切分策略，作者给出了两种实现方式：

第一种是协同边放置策略，这需要维护一张全局u顶点放置的历史纪录表，在执行贪心切分之前都要去查询这张表，在执行的过程中需要更新这张表。协同点切分的策略，它的特点是慢但点切分的质量高 ，

第二种方式是Oblivious的贪婪策略，它是一种近似的贪婪策略，不需要做全局的协同。贪婪算法的运行不依赖每一台机器，不需要维护全局的记录表，而是每台机器自己维护这张表，不需要做机器间的通信。这种策略速度快，但切分质量比较低。关于这种方式，论文只用了一段话来描述，具体如何操作明白。

具体同学们可以参考论文第8页最后一段文字描述。

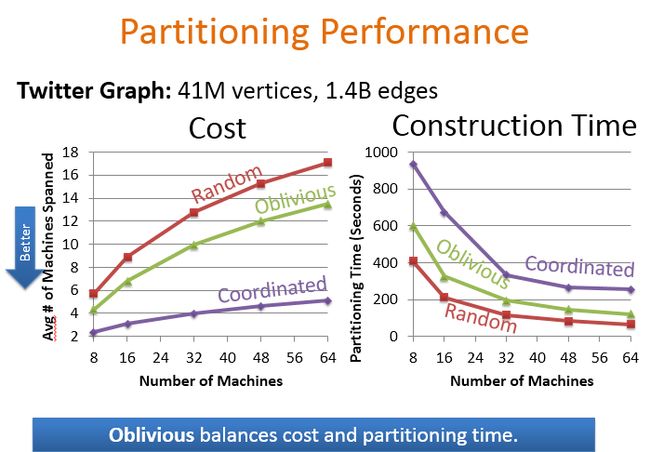
下面是对比这三种分区策略的性能，对比的是平均的机器跨度和构建时间。
协同的贪婪分区算法平局机器跨度最小，但构建时间最长。而随机策略构建时间短，但平局的机器跨度最大。而Oblivious的贪婪分区策略能够在平局机器跨度和构建时间上获得一个折中的性能。

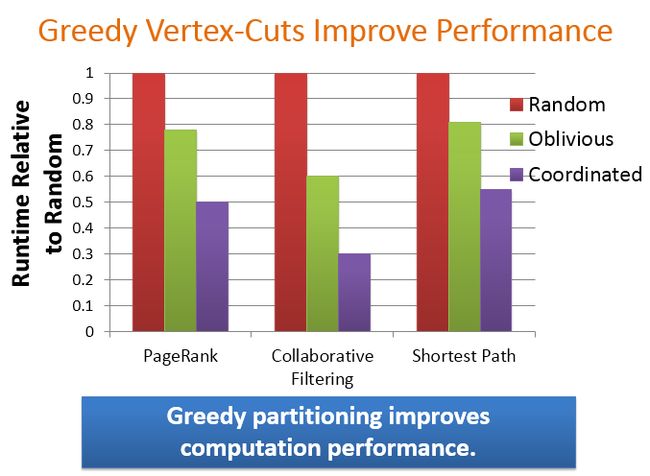
这里测试贪婪分区策略相对于随机分区策略的性能提升，纵坐标是相对于随机分区策略的时间，这里假设随机的时间开销为1，横坐标是PageRank、协同过滤算法、最短路径3种算法对应的时间开销。可以看出协同的贪婪分区策略的性能最佳，整体上贪婪分区能够提升计算性能。

这里PowerGraph还有一些其它的特性，包括3种执行模式。（全局同步，全局异步，可串行化异步）。还有一个增量Cacha的特性，具体这些特点可以参加论文第7节。

---

10. System Design

整个PowerGraph的架构是这样一个结构，最上层是PowerGraph 系统，它和GraphLab集成到一起，实现的接口是C++，利用HDFS进行数据的输入和输出，利用检查点来实现容错。

在这个系统上实现了许多经典算法，比如：
Alternating Least Squares 交替最小二乘法
Stochastic Gradient Descent随机梯度下降
SVD（Singular Value Decomposition）奇异值分解
Statistical Inference统计推断
Loopy Belief Propagation（LBP）循环信度传播算法
Gibbs Sampling吉布斯采样
Image stitching图像拼接
LDA（Latent Dirichlet Allocation）隐含狄利克雷分布文档主题生成模型



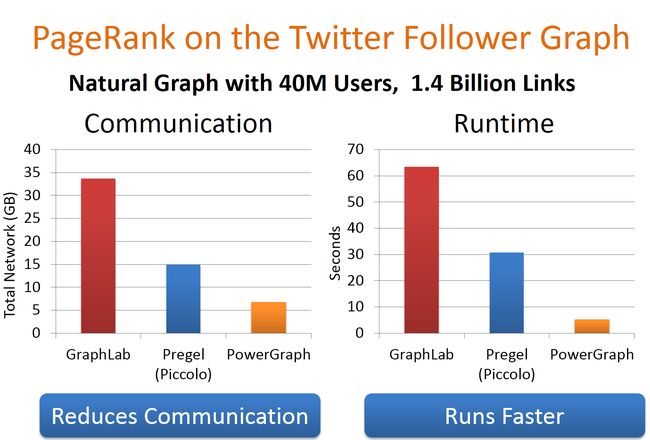
下面对比了Pregel、GraphLab和PowerGraph在运行PageRank算法上通信开销和执行的时间，可以看出PowerGraph不仅通信开销小而且运行时间短，对高纬度点有很强的健壮性。这时在人工合成的数据集上的一个性能。



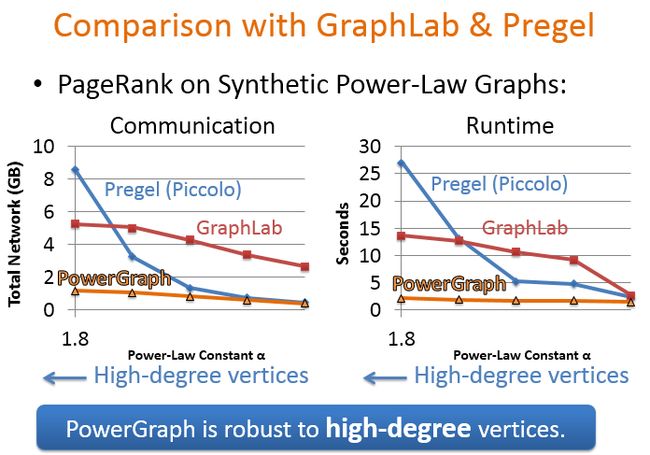
下面选用了真实的Twitter数据集进行时间。通信开销和运行时间相比GraphLab和Pregel都非常低。

作者还测试了PowerGraph可扩展性，利用目前可获取的最大公开数据集，Yahoo网页数据，14亿个网页，66亿条边，利用64个amazon的高性能节点，总共是1024个计算核。只需要30行用户端的代码，就可以达到7秒钟一次迭代，每秒能够处理1B条边。由此可见PowerGraph有非常好的扩展性。

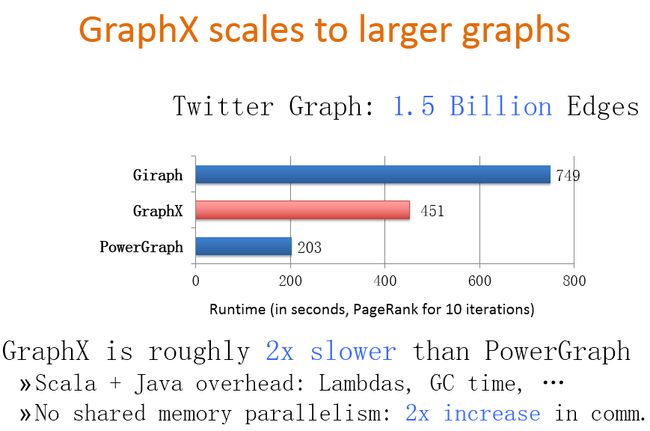
下面是我从2014年Grphax截过来的一页性能对比的PPT，可以看出Graphx的性能要比PowerGraph慢2倍左右，作者在这后面也给出了原应，因为PowerGraph是利用C++实现的，而GraphX是利用Scala语言实现，Java可能有很多开销。

---

11. Summary

---

【完】