【读书笔记】《信号与系统》第一章《信号与系统》（一）

1.关于信号的个人理解：

信号就是信号，它是一种广泛的物理现象，能够用很多不同的方法来表示，比如电容器电压可以产生电信号，汽车速度和时间的关系也可以描述为信号，拾音器能把声音转化为声信号在转化为电信号储存，再比如黑白图片各点亮度变化波形也是信号的直观表示。

2.连续信号和离散信号：

奥本海默在这本书里只考虑两种基本类型的信号：1.连续时间信号和2.离散时间信号

1.连续时间信号用t 表示，并且用（）圆括号将自变量包在里面

2.离散时间信号用x 表示，并且用  []  方括号将自变量包在里面，离散时间信号x[n]仅仅只在自变量的整数值上有定义。有时候为了更加强调这一点，就干脆将x[n]称为离散时间序列。（到这里都还挺好理解的）

离散时间信号的产生方式有两种，一种是自然采集过来就是离散的，比如有关人口统计学中的一些数据（人是一个一个的没法作为连续信号，当然在某种取值产生信号的方式下也可以作为连续信号），再一种是对连续时间信号进行采样得到的离散时间信号。「这个也很好理解，比如一个正弦波，你每隔π/2的时间对它进行采样，你得到的信号就是一个周期为π的[0,1,0,-1]的信号了」

3.信号能量与功率：

这一小节没什么意义，就是信号在使用者想要研究的时间上的积分，别问，问就是积。

要是是在无限上的积分那就具体情况具体讨论，后面的章节有相关的例子。

4.自变量变换：

第一种是时移，我理解为信号波向后传递n0个单位长度，简单理解为平移也可以。x[n]&x[n-n0]形状是一样的，n0大于0时，就是x[n]向右传递了。

第二种是时间反转，对于连续信号和离散信号，x[-n]就是x[n]关于n=0这条轴翻转得到的。

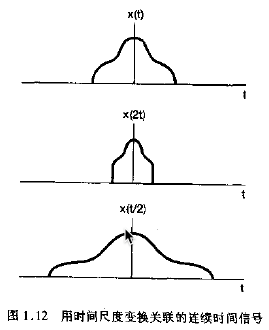
第三种是尺度变换，用音频举例子的话，x(t)就是一首歌，x(2t)两倍速播放，x(t/2)0.5倍速播放。具体来说就是我们有一个信号波，现在把它尺度变换变成x(2t),那么原来的t=t0处就要变成原来t=2t0处的对应的值。（下图是我从书上抄的，不是我自己画的，如果有关方侵权请联系我把这个图删除）

5.周期信号：

周期信号这一节主要理解周期信号的定义：一个周期连续时间信号x(t)​具有这样的性质，即存在一个正值的T，对全部t来说，有

x（t） = x （t + T）

就是说，一个信号，通过上一个小节中提到的时移T后其值不变。挺好理解的​​​​​​，背下来就行了。

但是书上提到了，周期信号是很理想的情况，大多数时候信号都是有能量的，而能量在传递过程中衰减，信号就在时移过程中改变了，也就是说下一个T时间内的信号波比此时是要弱的。ez.

因为周期信号的周期可以是T, 2T, 3T, 所以使周期信号成立的最小正值T被称为基波周期T0。

x(t)为常数是不对基波周期进行定义，没有意义，谁让你定义，那必是杠精。然后对于任何T来说x(t)都是周期的。

离散时间信号差不多，定义：如果一个离散时间信号x[n]时移一个N后其值不变，即对全部n值有

x[n] = x[n + N]

则x[n]是周期的，周期为N，N为某一个正整数。

其他的和上面连续时间信号差不多，理解就行。

6.偶信号和奇信号：

偶信号和奇信号就是一个对称性问题。

偶信号：如果一个信号x(t)以原点为轴，反转后不变，那就是偶信号。x(-t) = x(t)

奇信号：t=0时奇信号必须为0，x(-t) = -x(t)

接下来这个点很6：任何信号都能分解成两个信号之和，其一为偶信号（偶部），另一位奇信号（奇部）

偶部Ev|x(t)| = 1/2 [x(t)+x(-t)]

奇部Od|x(t)| = 1/2 [x(t)-x(-t)]

x(-t)就是x(t)反转，也不用管对不对称，那个是判断奇偶性的。