那些经典算法：AC自动机

第一次看到这个名字的时候觉得非常高级，深入学习就发现，AC就是一种多模式字符串匹配算法。前面介绍的BF算法，RK算法，BM算法，KMP算法都属于单模式匹配算法，而Trie树是多模式匹配算法，多模式匹配算法就是在一个主串中查找多个模式串，举个最常用的例子，比如我们在论坛发表评论或发帖的时候，一般论坛后台会检测我们发的内容是否有敏感词，如果有敏感词要么是用***替换，要么是不让你发送，我们评论是通常是一段话，这些敏感词可能成千上万，如果用每个敏感词都在评论的内容中查找，效率会非常低，AC自动机中，主串会与所有的模式串同时匹配，这时候就可以利用AC自动机这种多模式匹配算法来完成高效的匹配，

一 AC自动机算法原理

AC自动机算法是构造一个Trie树，然后再添加额外的失配指针。这些额外的适配指针准许在查找字符串失败的时候进行回退（例如在Trie树种查找单词bef失败后，但是在Trie树种存中bea这个单词，失配指针会指向前缀be），转向某些前缀分支，免于重复匹配前缀，提高算法效率。
常见于IDS软件或病毒检测软件中病毒特征字符串，可以构建AC自动机，在这种情况下，算法的时间复杂度为输入字符串的长度和匹配数量之和。

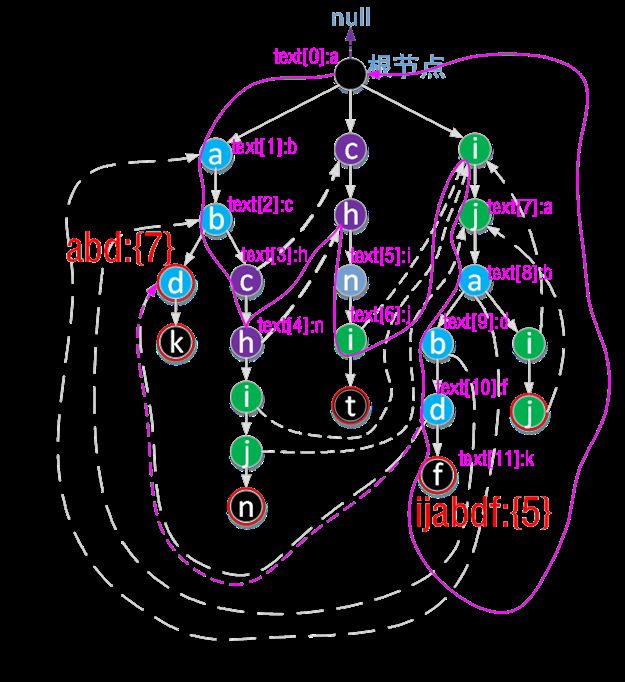
假设现有模式字符串集合：{abd,abdk, abchijn, chnit, ijabdf, ijaij} 构建AC自动机如下：

AC自动机图来自互联网

说明：

• 根节点不存在任何字符，根节点的fail指针为null。
• 虚线表示该节点的fail指针，所有模式串中字符串最后一个字符节点外面用红圈表示，说明是匹配上的字符串。
• 每个节点都有fail指针，为了方便图中未画出根节点的fail虚线。
  每个节点的fail指针表示从根节点到该节点所组成字符序列中所有后缀和目标的模式串集合中所有前缀 两者中最长的公共部分。
  举例：
  图中，从根节点到目标字符串“ijabdf”中d组成字符序列“ijabd”的所有后缀在整个模式串中：
  {abd,abdk, abchijn, chnit, ijabdf, ijaij}的所有前缀中，最长的公共部分就是abd，所以“ijabdf”中d的fail指针就是指向abd中的d。
  https://www.cnblogs.com/nullzx/p/7499397.html

二 AC自动机运行过程

1）当前指针curr指向AC自动机的根节点：curr=root。
2）从文本串中读取（下）一个字符。
3）从当前节点的所有孩子节点中寻找与该字符匹配的节点：

• 如果成功：判断当前节点以及当前节点fail指向的节点是否表示字符串结束，则将匹配的字符串（从根节点到结束节点）保存。curr指向孩子节点，继续执行步骤2。
• 如果失败执行步骤4

4）若fail == null，则说明没有任何子串为输入字符串的前缀，这时设置curr = root，执行步骤2.
若fail != null,则将curr指向 fail节点，指向步骤3。
理解起来比较复杂，找网上的一个例子，假设文本串text = “abchnijabdfk”。
查找过程如下：

AC自动机执行过程

说明如下：
1）按照字符串顺序依次遍历到：a-->b-->c-->h ,这时候发现文本串中下一个节点n和Trie树中下一个节点i不匹配，且h的fail指针非空，跳转到Trie树中ch位置。
注意c-->h的时候判断h不为结束节点，且c的fail指针也不是结束节点。
2）再接着遍历n-->i,发现i节点在Trie树中的下一个节点找不到j，且有fail指针，则继续遍历，
遍历到d的时候要注意，d的下一个匹配节点f是结束字符，所以得到匹配字符串：ijabdf，且d的fail节点也是d，且也是结束字符，所以得到匹配字符串abd，不过不是失败的匹配，所以curr不跳转。

三 AC自动机的构造过程

先将目标字符串插入到Trie树种，然后通过广度有限遍历为每个节点的所有孩子节点找到正确的fail指针。
具体步骤如下：
1）将根节点的所有孩子节点的fail指针指向根节点，然后将根节点的所有孩子节点依次入队列。
2）若队列不为空：
2.1）出列一个字符，将出列的节点记为curr，failTo表示curr的
fail指针，即failTo = curr.fail 。
2.2) 判断curr.child[i] == failTo.child[i]是不是成立：
成立：curr.child[i].fail = failTo.child[i]
因为当前字符串的后缀和Tire树的前缀最长部分是到fail，
且子字符和failTo的下一个字符相同，则fail指针就是
failTo.child[i]。
不成立： 判断failTo是不是为null是否成立：
成立： curr.child[i].fail = root = null。
不成立： failTo = failTo.fail 继续2.2
curr.child[i]入列，再次执行步骤2）。
3）队列为空结束。

四 实例理解

每个结点的fail指向的解决顺序是按照广度有限遍历的顺序完成的，或者说层序遍历的顺序进行，我们根据父结点的fail指针来求当前节点的fail指针。

AC自动机查找演示A

理解fail指针的含义：表示从根节点到该节点所组成字符序列的所有后缀和 整个模式字符串集合即整个Trie树中 所有前缀 两者中的最长公共部分。

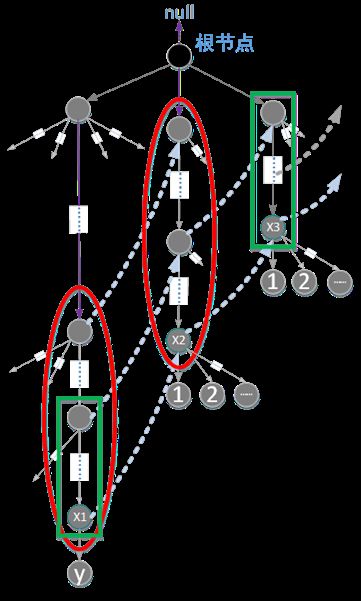
上图为例，我们要解决y节点的fail指针问题，已经知道y节点的父节点x1的fail是指向x2的，根据fail指针的定义，我们知道红色椭圆中的字符串序列肯定相等，而且是最长的公共部分。依据y.fail的含义，如果x2的某个孩子节点和节点y表示的表示的字符相等，y的fail就指向它。
如果x2的孩子节点中不存在节点y表示的字符。由于x2.fail指向x3，根据x2.fail的含义，我们知道绿色框中的字符序列是相同的。显然如果x3的某个孩子和节点y表示字符相等，则y.fail就指向它。

如果x3的孩子节点不存在节点y表示的字符，我们重复这个步骤，直到xi的fail节点指向null，说明我们达到顶层，只要y.fail= root就可以了。
构造过程就是知道当前节点的最长公共前缀的情况下，去确定孩子节点的最长公共前缀。

4.1 确定图中h节点fail指向的过程

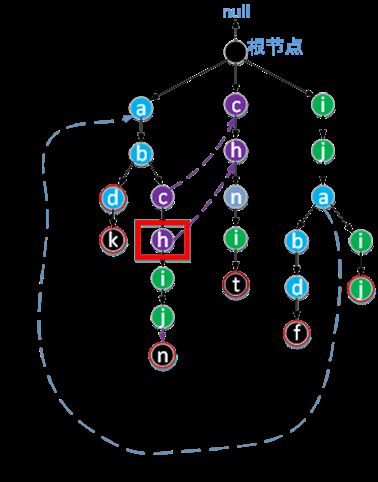
下图中，每个节点都有fail虚线，指向根节点的虚线没画出，求图中c的孩子节点h的fail指向：

原图

H的Fail确定图

原图中，深蓝色的框出来的是已经确定fail指针的，求红色框中h节点的fail指针。
这时候，我们看下h的父亲节点c的fail指针指向，为ch中的c（这表示abc字符串的所有后缀bc和c和Trie树的所有前缀中最长公共部分为c），且这个c节点的孩子节点中有字符为h的字符，所以图中红色框中框出的h节点的fail指针指向 ch字符串中的h。

4.2 确定图中i.fail指向

原图2

I的Fail指针

求红色框中i的fail指针指向，上图中，我们可以看到i的父亲节点h的指向为ch中的h，（也就是说我们的目标字符串结合中所有前缀和字符序列abch的所有后缀在Trie树中最长前缀为ch。）我们比较i节点和ch中的h的所有子节点，发现h只有一个n的子节点，所以没办法匹配，那就继续找ch中h的fail指针，图中没画出，那么就是它的fail指针就是root，然后去看root所有子节点中有没有和i相等的，发现最右边的i是和我们要找的i相等的，所以我们就把i的fail指针指向i，如后面的图。

五 代码实现

import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Map.Entry;
 
public class AhoCorasickAutomation {
    /*本示例中的AC自动机只处理英文类型的字符串，所以数组的长度是128*/
    private static final int ASCII = 128;
     
    /*AC自动机的根结点，根结点不存储任何字符信息*/
    private Node root;
     
    /*待查找的目标字符串集合*/
    private List target;
     
    /*表示在文本字符串中查找的结果，key表示目标字符串， value表示目标字符串在文本串出现的位置*/
    private HashMap> result;
     
    /*内部静态类，用于表示AC自动机的每个结点，在每个结点中我们并没有存储该结点对应的字符*/
    private static class Node{
         
        /*如果该结点是一个终点，即，从根结点到此结点表示了一个目标字符串，则str != null, 且str就表示该字符串*/
        String str;
         
        /*ASCII == 128, 所以这里相当于128叉树*/
        Node[] table = new Node[ASCII];
         
        /*当前结点的孩子结点不能匹配文本串中的某个字符时，下一个应该查找的结点*/
        Node fail;
         
        public boolean isWord(){
            return str != null;
        }
         
    }
     
    /*target表示待查找的目标字符串集合*/
    public AhoCorasickAutomation(List target){
        root = new Node();
        this.target = target;
        buildTrieTree();
        build_AC_FromTrie();
    }
     
    /*由目标字符串构建Trie树*/
    private void buildTrieTree(){
        for(String targetStr : target){
            Node curr = root;
            for(int i = 0; i < targetStr.length(); i++){
                char ch = targetStr.charAt(i);
                if(curr.table[ch] == null){
                    curr.table[ch] = new Node();
                }
                curr = curr.table[ch];
            }
            /*将每个目标字符串的最后一个字符对应的结点变成终点*/
            curr.str = targetStr;
        }
    }
     
    /*由Trie树构建AC自动机，本质是一个自动机，相当于构建KMP算法的next数组*/
    private void build_AC_FromTrie(){
        /*广度优先遍历所使用的队列*/
        LinkedList queue = new LinkedList();
         
        /*单独处理根结点的所有孩子结点*/
        for(Node x : root.table){
            if(x != null){
                /*根结点的所有孩子结点的fail都指向根结点*/
                x.fail = root;
                queue.addLast(x);/*所有根结点的孩子结点入列*/
            }
        }
         
        while(!queue.isEmpty()){
            /*确定出列结点的所有孩子结点的fail的指向*/
            Node p = queue.removeFirst();
            for(int i = 0; i < p.table.length; i++){
                if(p.table[i] != null){
                    /*孩子结点入列*/
                    queue.addLast(p.table[i]);
                    /*从p.fail开始找起*/
                    Node failTo = p.fail;
                    while(true){
                        /*说明找到了根结点还没有找到*/
                        if(failTo == null){
                            p.table[i].fail = root;
                            break;
                        }
                         
                        /*说明有公共前缀*/
                        if(failTo.table[i] != null){
                            p.table[i].fail = failTo.table[i];
                            break;
                        }else{/*继续向上寻找*/
                            failTo = failTo.fail;
                        }
                    }
                }
            }
        }
    }
     
    /*在文本串中查找所有的目标字符串*/
    public HashMap> find(String text){
        /*创建一个表示存储结果的对象*/
        result = new HashMap>();
        for(String s : target){
            result.put(s, new LinkedList());
        }
         
        Node curr = root;
        int i = 0;
        while(i < text.length()){
            /*文本串中的字符*/
            char ch = text.charAt(i);
             
            /*文本串中的字符和AC自动机中的字符进行比较*/
            if(curr.table[ch] != null){
                /*若相等，自动机进入下一状态*/
                curr = curr.table[ch];
                 
                if(curr.isWord()){
                    result.get(curr.str).add(i - curr.str.length()+1);
                }
                 
                /*这里很容易被忽视，因为一个目标串的中间某部分字符串可能正好包含另一个目标字符串，
                 * 即使当前结点不表示一个目标字符串的终点，但到当前结点为止可能恰好包含了一个字符串*/
                if(curr.fail != null && curr.fail.isWord()){
                    result.get(curr.fail.str).add(i - curr.fail.str.length()+1);
                }
                 
                /*索引自增，指向下一个文本串中的字符*/
                i++;
            }else{
                /*若不等，找到下一个应该比较的状态*/
                curr = curr.fail;
                 
                /*到根结点还未找到，说明文本串中以ch作为结束的字符片段不是任何目标字符串的前缀，
                 * 状态机重置，比较下一个字符*/
                if(curr == null){
                    curr = root;
                    i++;
                }
            }
        }
        return result;
    }
     
     
    public static void main(String[] args){
        List target = new ArrayList();
        target.add("abcdef");
        target.add("abhab");
        target.add("bcd");
        target.add("cde");
        target.add("cdfkcdf");
         
        String text = "bcabcdebcedfabcdefababkabhabk";
         
        AhoCorasickAutomation aca = new AhoCorasickAutomation(target);
        HashMap> result = aca.find(text);
         
        System.out.println(text);
        for(Entry> entry : result.entrySet()){
            System.out.println(entry.getKey()+" : " + entry.getValue());
        }
         
    }
}