zzu数学 实验八物理现象之模拟电场线

zzu数学 实验八物理现象之模拟电场线

大家都学过高中物理，看到两个点电荷之间的电场线，等势线等，有没想过这些图是怎么画出来的？如果是随手画出来的，为什么会这么精准？今天就带大家走进，电场线的绘制。提供两块代码作为对比参考。

• 代码一

                                  ** Physics **

          ** wave **

x0 = 0.0; v0 = 9.0; d = 0.05; k = 0.06; wave = {{1500*d, 0}};
Do[AppendTo[wave, {t*d, x0}]; a = -k*x0; v0 = v0 + a*d; x0 = x0 + v0*d,
  {t, 0, 1500}];
waveline = Line[wave];
Show[Graphics[waveline, AspectRatio -> Automatic]]


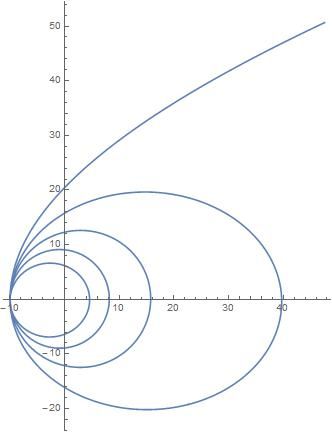
   ** Newton to  Kepler **

x0 = -10.0; y0 = 0; u0 = 0; v0 = 85; k = 40000; d = 0.006; p = {{0, 0}};
AppendTo[p, {x0, y0}]; n = 2;
While[! (p[[-2, 2]] < 0 && p[[-1, 2]] >= 0) && n <= 8000,
  r = (x0^2 + y0^2)^(0.5); a = -k*x0/(r^3); b = -k*y0/(r^3);
  u1 = u0 + a*d; v1 = v0 + b*d; x1 = x0 + u1*d; y1 = y0 + v1*d;
  AppendTo[p, {x1, y1}]; u0 = u1; v0 = v1; x0 = x1; y0 = y1; n++];
  q = {Line[p]}; Print[n];
Do[AppendTo[q, Line[{{0, 0}, p[[i]]}]], {i, 2, n, 80}];
Show[Graphics[q], AspectRatio -> Automatic] 

x0 = -10; y0 = 0; u0 = 0; v0 = 50; k = 40000; d = 0.006; tm = {}; t1 = 0;
p = {{x0, y0}};
Do[r = (x0^2 + y0^2)^(0.5); a = -k*x0/(r^3); b = -k*y0/(r^3);
  u1 = u0 + a*d; v1 = v0 + b*d; x1 = x0 + u1*d; y1 = y0 + v1*d;
  AppendTo[p, {x1, y1}]; u0 = u1; v0 = v1; x0 = x1; y0 = y1;
  If[p[[-2, 2]] < 0 && p[[-1, 2]] >= 0, v = v0 + 10; v0 = v; u0 = 0]
  , {n, 1, 1400}];
t = ListPlot[p, PlotJoined -> True, AspectRatio -> Automatic]     

   ** Kepler to Newton **

a = 25; b = 12; c = Sqrt[a^2 - b^2];
g1[t_] := a*Cos[t] - c; g2[t_] := b*Sin[t];
pic0 = ParametricPlot[{g1[t], g2[t]}, {t, 0, 2 Pi}, AspectRatio -> Automatic];
n = 180;
d = N[Pi/n]; ac = {}; p = {}; f = {};
Do[x0 = g1[k - d]; y0 = g2[k - d];
    x1 = g1[k]; y1 = g2[k];
    x2 = g1[k + d]; y2 = g2[k + d];
 t0 = x0*y1 - x1*y0; t1 = x1*y2 - x2*y1;
 ax = ((x2 - x1)/t1 - (x1 - x0)/t0)/((t0 + t1)/2);
 ay = ((y2 - y1)/t1 - (y1 - y0)/t0)/((t0 + t1)/2);
 a1 = (ax*ax + ay*ay)^(0.5); r2 = x1*x1 + y1*y1; c1 = a1*r;
 AppendTo[f, {r2, a1}];
 AppendTo[ac, Line[{{x1, y1}, {x1 + (r2^0.5)*ax/a1, y1 + (r2^0.5)*ay/a1}}]],
 {k, 0, 2 Pi, d}]

ac1 = Table[ac[[i]], {i, 1, 2 n, 20}];
Show[pic0, Graphics[ac1], AspectRatio -> Automatic]

pic2 = ListPlot[Table[{f[[i, 1]], 1/f[[i, 2]]}, {i, 1, n}]]

pic1 = ListPlot[f]

p = Table[f[[i, 1]]*f[[i, 2]], {i, 1, 2 n}];
pic3 = ListPlot[p, PlotJoined -> True];
{Sort[p][[1]], Sort[p][[-1]]}

                  ** Light **

f0[x_] := 2 - Sqrt[4 - x^2];
p0 = Plot[f0[x], {x, 0, 2}, PlotStyle -> {RGBColor[1, 0, 0]}, 
  AspectRatio -> Automatic]


t0 = {}; Do[AppendTo[t0,
  Line[{{k, 2}, {k, f0[k]}, {0, (f0[k]^2 + k^2 - 4)/(2 f0[k] - 4)}}]], {k, 0, 
  0.5, 0.1}];
Show[p0, Graphics[t0]]


t1={};Do[a=(2-f0[k])/k;b=1;c=-2;l=-(b+c)/(a^2+b^2);u=2a*l-k;v=1+2b*l-f0[k];
         t=(2-f0[k])/v;
        AppendTo[t1, Line[{{0,1},{k,f0[k]},{k+t*u,f0[k]+t*v}}]],{k,0.1,1.9,0.1}];
Show[p0,Graphics[t1]]

x1 = 0.01; y1 = 0; s = 0.005; t1 = {{0, 0}, {x1, y1}};
Do[r = Sqrt[x1^2 + (1 - y1)^2]; u = x1/r; v = 1 - (1 - y1)/r;
   r1 = Sqrt[u^2 + v^2];
      x2 = x1 + s*u/r1; y2 = y1 + s*v/r1; AppendTo[t1, {x2, y2}];
     x1 = x2; y1 = y2,
     {m, 1, 1200}];
p1 = ListPlot[t1, PlotJoined -> True, AspectRatio -> Automatic]

t2 = {}; Do[
 AppendTo[t2, Line[{{0, 1}, t1[[k]], {t1[[k, 1]], 4.2}}]], {k, 1, 1200, 60}];
Show[p1, Graphics[t2], AspectRatio -> Automatic]

k = t1[[500, 2]]/t1[[500, 1]]^2;
p3 = Plot[k*x^2, {x, 0, 3.5}, PlotStyle -> {RGBColor[0.1, 0.8, 0.1]}];
Show[p1, p0, p3, AspectRatio -> Automatic]

** electroic field **

pic = {Line[{{-5, 0}, {5, 0}}], Line[{{0, -5}, {0, 5}}]};
d = 0.05; e = -1;
Do[x0 = -2 + 0.5*Cos[k]; y0 = 0.5*Sin[k];
  lin1 = {{-2, 0}, {x0, y0}}; lin2 = {{2, 0}, {-x0, y0}};
  While[x0 > -5 && x0 <= 0 && Abs[y0] <= 5.15,
      r1 = Sqrt[(x0 + 2)^2 + y0^2]; r2 = Sqrt[(x0 - 2)^2 + y0^2];
      u = (x0 + 2)/(r1^3) + e (x0 - 2)/(r2^3);
      v = y0/(r1^3) + e*y0/(r2^3); w = Sqrt[u^2 + v^2];
      x1 = x0 + d*u/w; y1 = y0 + d*v/w;
   AppendTo[lin1, {x1, y1}]; AppendTo[lin2, {-x1, y1}]; x0 = x1; y0 = y1];
  AppendTo[pic, Line[lin1]]; AppendTo[pic, Line[lin2]],
  {k, 0, 2 Pi, Pi/12}];
 pic4 = Show[Graphics[pic], AspectRatio -> Automatic]

pc = {}; 
Do[d = 0.1 pm;
  Do[x0 = k; y0 = 0.0; lin3 = {{x0, y0}}; lin4 = {{x0, -y0}};
   While[y0 >= 0 && y0 <= 5 && Abs[x0] <= 5.2, 
       r1 = Sqrt[(x0 + 2)^2 + y0^2]; r2 = Sqrt[(x0 - 2)^2 + y0^2];
       u = (x0 + 2)/(r1^3) + e*(x0 - 2)/(r2^3);
       v = y0/(r1^3) + e*y0/(r2^3); w = Sqrt[u^2 + v^2];
       x1 = x0 - d*v/w; y1 = y0 + d*u/w;
    AppendTo[lin3, {x1, y1}]; AppendTo[lin4, {x1, -y1}];
    x0 = x1; y0 = y1];
   AppendTo[pc, Line[lin3]];
   AppendTo[pc, Line[lin4]],
   {k, -1.8, 1.8, 0.4}],
  {pm, -1, 1, 2}];
Do[d = 0.1 pm;
  Do[x0 = 0.0; y0 = k; lin3 = {{x0, y0}}; lin4 = {{x0, -y0}};
   While[y0 >= 0 && y0 <= 5 && Abs[x0] <= 5.2, 
       r1 = Sqrt[(x0 + 2)^2 + y0^2]; r2 = Sqrt[(x0 - 2)^2 + y0^2];
       u = (x0 + 2)/(r1^3) + e*(x0 - 2)/(r2^3);
       v = y0/(r1^3) + e*y0/(r2^3); w = Sqrt[u^2 + v^2];
       x1 = x0 - d*v/w; y1 = y0 + d*u/w;
    AppendTo[lin3, {x1, y1}]; AppendTo[lin4, {x1, -y1}];
    x0 = x1; y0 = y1];
   AppendTo[pc, Line[lin3]];
   AppendTo[pc, Line[lin4]],
   {k, 0.05, 4.8, 0.4}],
  {pm, -1, 1, 2}];
pic5 = Show[Graphics[pc], pic4, AspectRatio -> Automatic] 

             ** differential equation   dy/dx = x^2 + y^2  **

Clear[f];
f[x_, y_] := x^2 + y^2;
curves = {Line[{{-5, 0}, {5, 0}}], Line[{{0, -5}, {0, 5}}]};
Do[d = 0.05 pm;
  Do[x0 = 0.2 k; y0 = 0; points = {{x0, y0}};
     While[Abs[y0] < 5,
        r = Sqrt[1 + (f[x0, y0])^2];
        x1 = x0 + d/r; y1 = y0 + d*f[x0, y0]/r;
        AppendTo[points, {x1, y1}];
        x0 = x1; y0 = y1];
      AppendTo[curves, Line[points]],
   {k, -25, 25, 2.5}],
  {pm, -1, 1, 2}];
pic1 = Show[Graphics[curves], AspectRatio -> Automatic]

curves2 = {Line[{{-5, 0}, {5, 0}}], 
  Line[{{0, -5}, {0, 5}}]}; curves3 = {Line[{{-5, 0}, {5, 0}}], 
  Line[{{0, -5}, {0, 5}}]};
d = 0.05;
Do[x0 = 0.2 k; y0 = -5; points1 = {{x0, y0}}; points2 = {{-x0, -y0}};
    While[Abs[y0] <= 5,
       r = Sqrt[1 + (f[x0, y0])^2];
       x1 = x0 + d/r; y1 = y0 + d*f[x0, y0]/r;
       AppendTo[points1, {x1, y1}]; AppendTo[points2, {-x1, -y1}];
       x0 = x1; y0 = y1];
     AppendTo[curves2, Line[points1]]; AppendTo[curves3, Line[points2]],
  {k, -25, 25}];
pic2 = Show[Graphics[curves2], AspectRatio -> Automatic];
pic3 = Show[Graphics[curves3], AspectRatio -> Automatic];
Show[pic2, pic3]

- 代码二

Clear[all];
EF[x_, y_] := Block[{}, a = 1; k = 1;
  A = {-a, 0};
  B = {0, a};
  FA = k*{x + a, y}/(((x + a)^2 + y^2)^(3/2));
  FB = -k*{x - a, y}/((x - a)^2 + y^2)^(3/2);
  F = FA + FB;
  F/Norm[F]]
m = 0.01;
Pics = {};
For[alpha = -Pi*3/4, alpha <= Pi*3/4, alpha = alpha + 0.3, 
 p0 = {-a, 0} + {m*Cos[alpha], m*Sin[alpha]};
 p = {p0};
 For[i = 1, Norm[Last[p] - {a, 0}] > m, i++, 
  temp = p[[i]] + m*EF[p[[i, 1]], p[[i, 2]]]; AppendTo[p, temp]];
 AppendTo[Pics, ListPlot[p, PlotStyle -> {PointSize[0.005], Black}]]]



EL[x_, y_] := Block[{}, eledir = EF[x, y];
  eleLinedir = {eledir[[2]], -(eledir[[1]])};
  eleLinedir = eleLinedir/Norm[eleLinedir]; eleLinedir]
m = 0.0005;
d = 0.2;
pics = {};
For[j = 1, -a + j*d < 0, j++, q0 = {-a + j*d, 0};
 q = {q0};
 For[i = 1, i <= 100000, i++, 
  temp = q[[i]] + m*EL[q[[i, 1]], q[[i, 2]]];
  AppendTo[q, temp];
  If[Last[q][[2]] > 0 && 
    0 < ArcTan[(Last[q][[2]])/(Last[q][[1]] + a)] < 0.05, Break[]]];
 points = 
  Graphics[ListPlot[q, PlotStyle -> {PointSize[0.005], Black}]];
 AppendTo[pics, points];]
m = 0.0005;
For[j = 1, a - j*d > 0, j++, q0 = {a - j*d, 0};
 q = {q0};
 For[i = 1, i <= 100000, i++, 
  temp = q[[i]] + m*EL[q[[i, 1]], q[[i, 2]]];
  AppendTo[q, temp];
  If[Last[q][[2]] > 0 && 
    0 < -ArcTan[(Last[q][[2]])/(Last[q][[1]] - a)] < 0.05, Break[]]];
 points = 
  Graphics[ListPlot[q, PlotStyle -> {PointSize[0.005], Black}]];
 AppendTo[pics, points];]

Show[{Pics, pics}, PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}}]

有时候会因为版本问题，导致有些命令使用不同，不出图甚至报错。我用的是Wolfram Mathematica 10.3 版本。