通过SVD对推荐系统的优化
首先有两个关键词,第一是SVD特征值分解,第二是基于相似度的推荐系统。
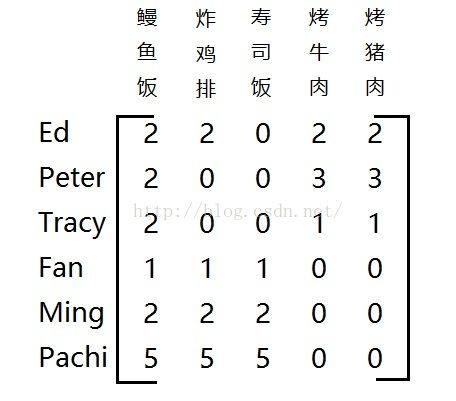
让我们虚构一个场景:一天晚上,你(Peter)需要晚餐的补给来继续你繁忙的工作,然而你并不知道吃什么而且并不想花时间去研究哪家饭店的哪道菜肴适合你。这个时候,你就需要一个推荐系统来帮助你选择,而且它有很高的可信度。假设你对吃过的菜肴做了评价,而没吃过的自然评价是0,于是就有一个属于你自己的菜肴评价记录。我们假设这个记录是这样的。每道菜都有一个评分,满分为5分。
我们看到你还未尝过炸鸡排和寿司饭,那么很显然你就很需要知道推荐系统对于这两道菜的评分是多少。假如你想吃其他菜的话,那么你也不需要推荐系统的帮助了,因为你已经知道自己对它们的评分,根据你以往的评分来选择就好了,推荐系统只会给你推荐你未尝过的菜,这是这个场景的前提。
推荐系统是根据什么来对物品进行评分的?那就是相关度,通过比较用户和用户之间的相关度或者物品与物品之间的相关度,我们就可以来预测未知物品的评分了。这个相关度怎么计算呢?对于相关度有三种可供选择的计算方法。
第一种 ,欧式距离。比如计算鳗鱼饭和炸鸡排的欧氏距离,
第二种,皮尔逊相关系数,它度量的是两个向量之间的相似度,但对于用户的量级不敏感,比如A用户对所有的菜肴都是5分,而B用户对所有的菜肴都是1分,那么皮尔逊相关系数认为这两个向量是相等的,取值为[-1,1]。
第三种,余弦相似度,它计算的是两个向量之间的夹角的余弦值如果两个向量的方向完全相同,则相似度为1。取值为[-1,1]。
根据具体的场景分析来选择相关度的度量方式。
在开始推荐系统的代码敲写之前,有一个重要的问题需要解决,是基于用户的相似度推荐还是基于物品的相似度推荐?这个答案很简单,想要计算时间少就是看谁的数量少。一般都是用户数量远远大于物品数量,所以是基于物品相似度推荐,当然具体的情况也要具体分析。这里的采用基于物品相似度的推荐。
推荐系统伪代码:
1.在评分记录矩阵中寻找该用户标记为0的值,即该用户没尝过的菜肴,将它们做成一个列表。
2.对每个没尝过的菜肴,计算这道菜肴与其他有评分的菜肴的相似度,并且根据相似度预计一个可能的评分 分数(计算主要在这块)。
3.根据评分分数进行排序并输出前N道菜肴供用户选择。
导入代码:
from numpy import *
from numpy import linalg as la 关于特征值的运算都集合在linalg包内
def loaddata():
return mat([[2, 2, 0, 2, 2],[2, 0, 0, 3, 3],[2, 0, 0, 1, 1],[1, 1, 1, 0, 0],[2, 2, 2, 0, 0],[5, 5, 5, 0, 0],[1, 1, 1, 0, 0]])
def ecludSim(inA,inB): #欧式相关度,1.0/(1.0+欧氏距离)
similiar=1.0/(1.0+la.norm(inA,inB)) #假定inA和inB都是列向量
return similiar
def pearsSim(inA,inB): #皮尔逊相关度
if len(inA) < 3: return 1.0 #如果inA的长度小于3,则是完全相关
similiar=0.5+0.5*corrcoef(inA,inB,rowvar=0)[0][1] #皮尔逊相关系数取值为[-1,1],所以需要0.5来归一化
def cosSim(inA,inB): #余弦相关度
num=float(inA.T*inB)
denom=la.norm(inA)*la.norm(inB)
similiar=0.5+0.5*(num/denom)
return similiar三种相关度计算方式代码,这里的inA和inB都是当作列向量计算,所以后续使用的时候应该注意转换。
def recommend(datamat,user,N=3,similiarmeans=cosSim,method=standest): #数据集,用户(行数),前N个推荐,相关度方法选择,推荐方法选择
noratingitems=nonzero(datamat[user,:].A == 0)[1] #输出这一行中为0的列位置
if len(noratingitems) == 0: print "all rates full" #如果这一行都没有为0,说明这些菜品这个用户都吃过,就没有推荐的意义。
scorelist=[]
for item in noratingitems:
scores=method(datamat,user,similiarmeans,item) #调用推荐方法得到分数
scorelist.append([item,scores])
return sorted(scorelist,key=lambda jj:jj[1],reverse=True)[:N] #按照第二列逆序排序并取前N个
def standest(datamat,user,similiarmeans,item): #标准协同过滤推荐方法
n=shape(datamat)[1] #取列数
similiartotal=0.0;ratsimiliartotal=0.0 #初始化相关度值,相关度分数值
for j in range(n):
userrating=datamat[user,j] #取user行中有数值的列
if userrating == 0: continue
lop=nonzero(logical_and(datamat[:,item].A>0,datamat[:,j].A>0))[0] #并且其他行的这一列也有数值
if len(lop) == 0: similiar=0.0
else:similiar=similiarmeans(datamat[lop,item],datamat[lop,j]) #计算相关度,这里采用余弦相关度
print "the item %d with the j %d is similiar %f:" % (item,j,similiar)
similiartotal += similiar #累加所有相关度
ratsimiliartotal += similiar*userrating #累加所有相关度分数值
if similiartotal == 0:return 0
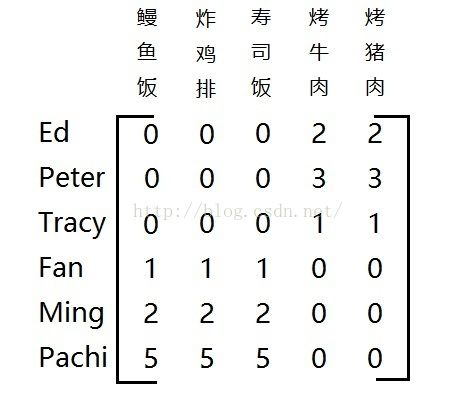
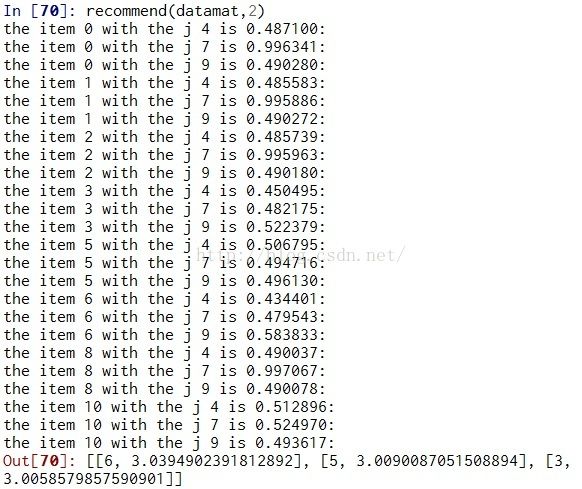
return ratsimiliartotal/similiartotal现在看下运行结果,Peter所在行数为1,所以我们这么运行:
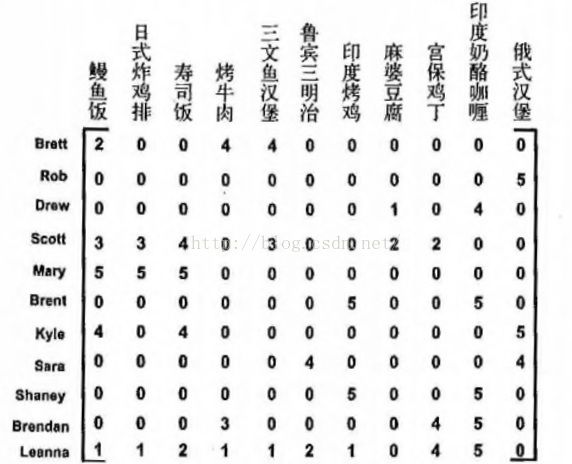
目前为止,我们已经完成了简单的推荐系统的构建,但是对于由大量稀疏矩阵构成的记录,我们仍用这一套推荐系统那就是太浪费计算空间了,我们应该在数学上将多维的矩阵转化为低维的矩阵,从而大大降低了储存空间和计算量,SVD特征值分解就是为了降维而准备的。我们再看下一个评分记录。
我们看到这个评分记录矩阵中有很多个0,这就是稀疏矩阵。稀疏矩阵中存在着大量的噪声和冗余信息,从而带来了整个推荐系统的工作空间的增加和运算量的增加,但是效率上却非常的低。因此我们十分有必要去降低矩阵的维度,只保留有用的信息,去除噪声,节省空间。那么SVD是怎么做到这些的?
首先了解一下奇异值的分解公式:M = UΣVT
Σ就是由奇异值组成的对角矩阵,对角元素就是奇异值。任何矩阵都可以分解为三个矩阵。V 表示了原始域的
标准正交基,U 表示经过 M 变换后的co-domain的标准正交基,Σ表示了V 中的向量与u 中相对应向量之间的关系。
理解起来可能有些抽象,举个例子。
假如对这个矩阵做奇异值分解后,会得到两个奇异值,这说明这个矩阵中隐含着两种相关概念或主题,我们对这段评分记录做分析,发现前三个人吃的都是美式菜肴,而后三个人吃的都是日式料理,这就是隐藏在矩阵里的某两种主题或概念。这就是奇异值的作用,从稀疏矩阵的噪声里提取相关特征。那么我们是怎样通过奇异值降维呢?
当Σ里的有些对角元素即奇异值太小时,我们认为此时该奇异值可以忽略,仅保留前N个奇异值即可,在具体应用这样做
可认为是数据集中仅有N个重要特征,而剩余的都是噪声或冗余特征,我们通过提取重要特征来降维,这跟PCA有点类似了。
那么怎么知道这N个奇异值是我们需要保存的呢?有一种方法就是保留矩阵里90%的能量信息,具体的解释在代码里。
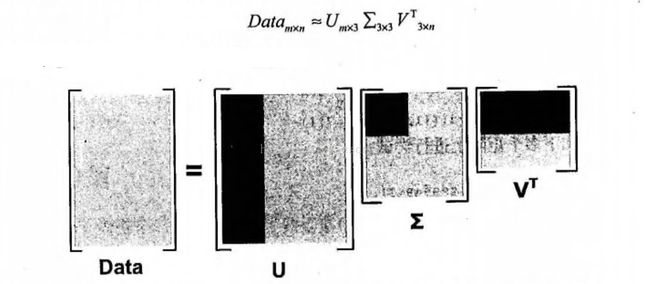
在导入代码之前,我们通过一张图来形象理解通过奇异值来提取重要特征的过程。
灰色区域是原矩阵通过特征值分解又重构的部分,而灰色区域则是只取前三个特征值重构的部分,它可以只提取重要特征,从而忽略噪声,这里并没有降维,而是去除噪声和冗余信息。
下面代码将展示如何通过SVD降维的过程。
def svdest(datamat,user,similiarmeans,item): #svd推荐方法
n=shape(datamat)[1]
similiartotal=0.0;ratsimiliartotal=0.0
U,sigma,VT=la.svd(datamat) #svd分解
sig4=mat(eye(4)*sigma[:4]) #取前n个特征值
xform=datamat.T*U[:,:4]*sig4.I #重构n个特征值的矩阵,.I为矩阵的逆,这里达成降维的效果。
for j in range(n):
userrating=datamat[user,j]
if userrating == 0 or j == item :continue
similiar=similiarmeans(xform[item,:].T,xform[j,:].T) #重构后的矩阵计算方法不一样,因为cosSim是列向量,所以需要转置
print "the item %d with the j %d is %f:" % (item,j,similiar)
similiartotal += similiar
ratsimiliartotal += similiar*userrating
if similiartotal == 0:return 0
return ratsimiliartotal/similiartotal
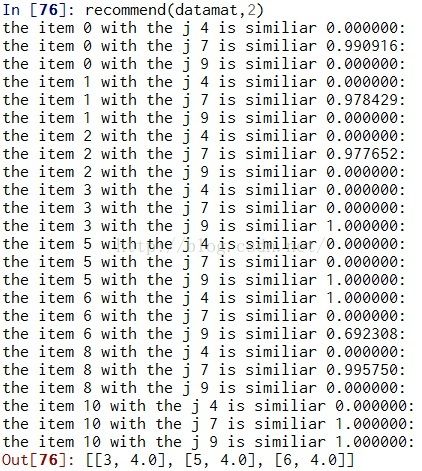
在运行这段代码之前,要将recommend里的形参method改为svdest。
以下是用普通推荐的运行结果
通过对比有无svd的推荐结果,其实这个数据用不用svd推荐的结果差不多,svd更略加精准些(手动搞笑),但是对于更多的稀疏矩阵来说svd的优化效果更明显。当然svd也是有副作用的,就是降低程序的运行效率,在越大的系统中越明显。