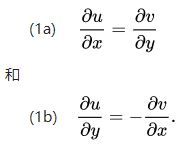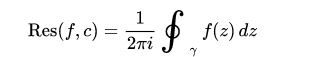复变函数基本概念总结

复变函数与解析函数

主辐角argz(-pi,pi), 辐角Argz=argz+2kpi;

零向量没有确定的方向角；

|z1z2|=|z1||z2|, Arg(z1z2)=Arg(z1)+Arg(z2);

De Moivre(棣莫弗公式)

邻域、内点、外点、边界点、开集（全是内点）、连通（任两个点可以多个折线段连接起来的点集称为连通的）区域（=开集+连通）；

简单曲线（只有一个重点【起点与终点重和的点】）、Jordan(若尔当)曲线（连续的简单闭曲线）、

连续（可用极限、或来描述）、一致连续；

解析函数：

解析点（邻域内处处可导的点）、解析函数（在区域的每一点都解析的函数）、奇点（不解析的点）、孤立奇点（在邻域内只有该点是奇点）；

柯西黎曼方程

；

全纯函数（holomorphic function）是复分析研究的中心对象；它们是定义在复平面C的开子集上的，在复平面C中取值的，在每点上皆复可微的函数。这是比实可微强得多的条件，暗示著此函数无穷可微并可以用泰勒级数来描述；

在复平面上，全纯函数与解析函数是等价的；

关于区分正则与全纯，正则是几何里的概念，也是指没有奇点，全纯是复分析里的概念；

初等解析函数：

指数函数、对数函数、幂函数、三角函数和双曲函数；

当z是复数时，|sinz|,|cosz|不是有界函数；

Cauchy（柯西）积分定理：是一个关于复平面上全纯函数的路径积分的重要定理。柯西积分定理说明，如果从一点到另一点有两个不同的路径，而函数在两个路径之间处处是全纯的，则函数的两个路径积分是相等的。另一个等价的说法是，单连通闭合区域上的全纯函数沿着任何可求长闭合曲线的积分是0；

复合闭路的Cauchy定理（复合闭路定理）（针对多连通区域）；

Cauchy积分公式；Cauchy导数公式（其实也是用来求积分的）；

牛顿-莱布尼兹公式（Newton-Leibniz formula）：

级数：

幂级数、Taylor级数、Laurent（洛朗）级数、（过段时间总结一下）；

调和函数；

函数在某点的某个邻域内可以展开成级数；

留数及其应用：

孤立奇点可分为三种情况：可去奇点（负幂次项全为零）、极点（含有限个负幂次项，至少一个）、本性奇点（含无穷多个）；（根据函数在z0点的去心邻域内的Laurent级数的展开式的系数来分的）；

单极点、m级极点、单零点、m级零点；

留数(其是函数在该点的邻域内的Laurent级数展开式中-1次项的系数)

；

留数基本定理：

假设{\displaystyle U}是复平面上的一个单连通开子集，{\displaystyle a_{1},\cdots ,a_{n}}是复平面上有限个点，{\displaystyle f}是定义在{\displaystyle U\setminus {a_{1},\cdots ,a_{n}}}的全纯函数。如果{\displaystyle \gamma }是一条把{\displaystyle a_{1},\cdots ,a_{n}}包围起来的可求长曲线，但不经过任何一个{\displaystyle a_{k}}，并且其起点与终点重合，那么：

{\displaystyle \oint _{\gamma }f(z)\,dz=2\pi i\sum _{k=1}^{n}\operatorname {I} (\gamma ,a_{k})\operatorname {Res} (f,a_{k}).}

如果γ是若尔当曲线，那么I(γ, a_k) = 1，因此：

{\displaystyle \oint _{\gamma }f(z)\,dz=2\pi i\sum _{k=1}^{n}\operatorname {Res} (f,a_{k}).}

在这里，Res(f, a_k)表示f在点a_k的留数，I(γ, a_k)表示γ关于点a_k的卷绕数。卷绕数是一个整数，它描述了曲线γ绕过点a_k的次数。如果γ依逆时针方向绕着a_k移动，卷绕数就是一个正数，如果γ根本不绕过a_k，卷绕数就是零。（copy于维基百科）

留数主要是用于积分；

保角映射（感觉很有意思，也很有用，但了解太少）：

保角性、保圆性、保对称性、

分式线性映射、

幂级数构成的映射可把角形域变成角形域；

指数函数构成的映射可把上平面域变成带形域；

引入Laplace变换的原因是为了弱化函数在负无穷到正无穷 上绝对可积的条件；