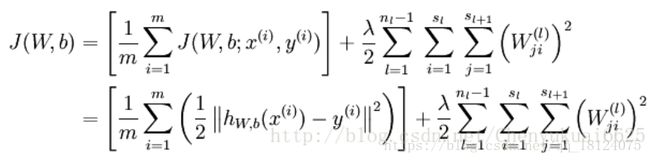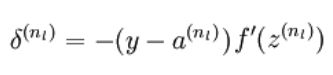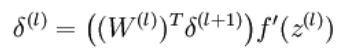Backpropagation

目录

残差的计算

前向传播与反向传播比较

神经网络全程回顾

---

链接：http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2015_2/Lecture/DNN%20backprop.pdf

今天我还是比较开心，因为解决了屯了很久的问题，即BP反向传播。很多人会觉得奇怪，它不就是链式法则、求偏导和梯度下降法更新吗？是的，确实知识点就这么多，但是这个东西让人细思极恐啊。比如：损失函数一般是均方误差、交叉熵，这些是因为我们在学习的时候好推导，看着方便。但在论文中损失函数并非这些简单的公式，如果换成其他的怎么办？与此同时，为了避免过拟合，在损失函数后面还会加一个惩罚项，一般都是二范，但是如果换成其他的，比如一范加二范，又改如何处理？大家都说神经网络是一个黑盒，里面是什么东西咋们不用管，但是这个黑盒也是人去设计的，要是里面出了问题，我们需要知道哪里的问题，这个反向传播具体的计算我们是不得不吃透。

现在，就让我们来学习反向传播吧。首先，需要的知识点：链式法则，求偏导。不会的就回去洗洗睡吧~~~哈哈哈

神经网络之所以牛逼是因为参数（权值和偏置）都是自动更新。所以主要的计算是通过损失函数去计算关于参数的偏导。这里，我们主要讲的是求权值的偏导。

损失函数对权值求偏导的公式，我们可以拆分成两个部分。对于第一个部分，Z表示激活函数的输入。当在第一层的时候，上一层的“输出”是input；在第一层之后的隐含层的时候，上一层的输出是神经元通过激活函数输出的结果，为a。a是早已经通过前向传播算出来了。

残差的计算

 

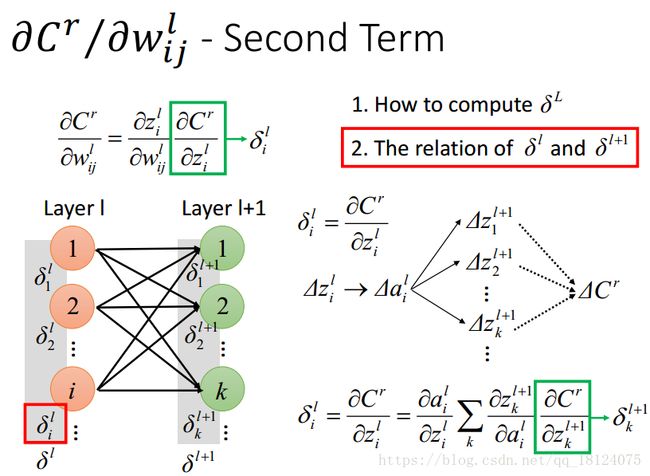
对于损失函数对权值的偏导公式第二个部分的计算我们称之为残差计算。关于残差的计算分为两步，第一步是求输出层的残差计算，第二步是根据输出层的残差以此类推前面的残差。

输出层的残差计算就是求关于损失函数对激活函数输入的偏导，由链式法则可以得到最后的结果，即如上图所示。这里，损失函数对最终输出结果的偏导计算是一个难点，因为不同的损失函数计算难度和相应的结果都是不同的。而对激活函数的偏导计算比较简单，公式都有模版，网上随便找就可以找到，需要注意一下，这里的激活函数括号里面的输入是激活函数的输入，而不是输出，别搞混了。

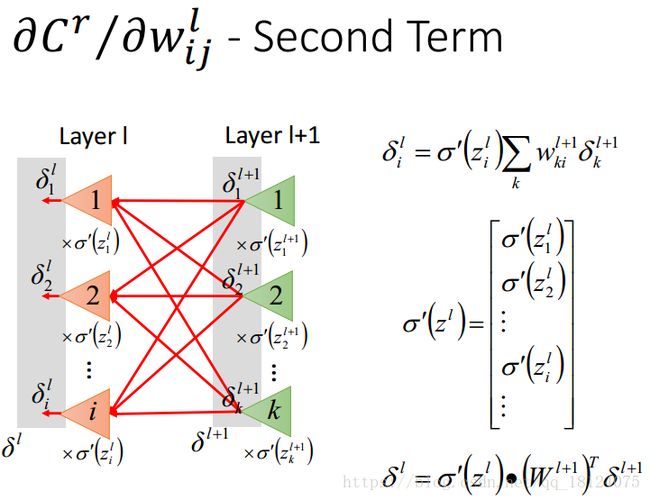
对于每一层的计算，我们可以把每一个神经元之间做对应的计算，即element-wise multiplication。这里的参数结果是一个vector。

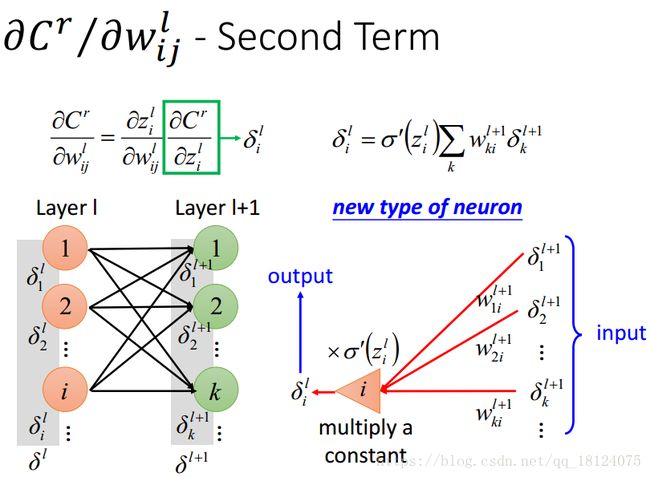
每一层之间的残差关系公式计算，我在其他的博客里面找过，都写得很复杂不好理解。这里，我们先理解那个求和公式，即l+1层中有k个神经元，所有有k个残差，中间红色连线部分的偏导比较简单，就是乘以权值。通过激活函数得到时候和上面一样，也需要对激活函数求偏导。这里逆向理解可能很复杂。

我们可以这么思考，我们最开始(l+1层)求的第一个残差是一组vector，当做网络的输入，输入乘以权值，传到激活函数那里（三角形部分），此时激活函数是一个常数值，并作为一个“放大器”的作用，所以把乘以权值之后的结果再乘上一个常数，从而得到l层的输出，即我们求得l层残差。所以说，前向传播是一个网络，反向传播也是一个网络。

前向传播与反向传播比较

向前传播：matrix*vector, non-linear transform

反向传播：matrix*vector, *scalar

异曲同工之妙

以下公式参考博客：https://blog.csdn.net/chenyukuai6625/article/details/74304992

神经网络全程回顾

假设训练的样本集包含m个样例，对于这个包含m个样本集的数据集而言，整体的代价函数应为：

上式关于J(W,b)定义中的第一项是一个均方差项。第二项是一个权重衰减项，其目的是减小权重的幅度，防止过度拟合。nl 表示神经网络的层数。sl表示第 l 层神经元个数，不包含偏置单元。

（1）进行前馈传导计算，利用前向传导公式，得到L2、L3直到输出层Ln的激活值。

（2）对输出层（第nl层），计算其残差：

（3）对于l=nl-1，nl-2，…，2的各层，计算其对应的残差：

（4）计算出每个神经元对应的偏导数值：

（5）将计算得到的偏导数值带入到权重W和偏置b对应的更新公式中去：

这里，我们需要注意的是在反向传播每一层中的权值和偏置都需要更新。这就是为什么去求每一层与每一层之间的残差。注意：第一层没有残差。

对于W和b的更新，如果后面有惩罚项，在每一层权值的更新中需要加入更新。