k_means python实现

k_means聚类算法实现

参考https://blog.csdn.net/taoyanqi8932/article/details/53727841进行了k_means聚类算法的实现
采用iris数据集进行了验证
iris数据集下载地址：https://archive.ics.uci.edu/ml/datasets/Iris

# -*- coding: utf-8 -*-
"""
Created on Sun Jan  5 15:33:48 2020
"""

# K-means
# K_means和KNN不同，
# KNN属于监督学习，每次为待分类向量选择距离最近的K个数据，按照出现最多的类别进行分类；
# k_means是一种无监督学习的聚类算法，通过选择K的质心将数据集分成K类
# k_means对于初始质心的选择敏感；
# K-Means是聚类算法中的最常用的一种，算法最大的特点是简单，好理解，运算速度快，
# 但是只能应用于连续型的数据，并且一定要在聚类前需要手工指定要分成几类
# 算法流程
"""选择K个点作为初始质心  
repeat  
    将每个点指派到最近的质心，形成K个簇  
    重新计算每个簇的质心  
until 簇不发生变化或达到最大迭代次数  """
from numpy import *
def dist_eclud(vec_a,vec_b):
    return sqrt(sum(pow(array(vec_a)-array(vec_b),2)))
    
def rand_cent(dataset,k):
    #dataset=array(dataset)
    n = shape(dataset)[1] # 数据集的特征数/维度
    centroids = mat(zeros((k,n)))
    for j in range(n-1):
        min_j = min(dataset[:,j])
        range_j = float(max(dataset[:,j])-min_j)
        centroids[:,j]=mat(min_j+range_j*random.rand(k,1))
        # np.random.rand(k,1)返回一个k×1维度的服从“0~1”均匀分布的随机样本值。
        #随机样本取值范围是[0,1)，不包括1。
    return centroids
    
def k_means(dataset,k,dist_meas=dist_eclud,create_cent=rand_cent):
    count =0 # 迭代次数
    m =  shape(dataset)[0] #样本数
    cluster = mat(zeros((m,2))-1) #分类结果，第一个维度是数据所属类别，第二个维度是距离该类别质心的距离
    centroids = create_cent(dataset,k) # 初始化K个中心
    cluster_changed=True
    while cluster_changed:
        count=count+1
        cluster_changed=False
        for i in range(m):
            minDist=inf
            minIndex = -1
            for j in range(k):
                dist_j_i = dist_meas(centroids[j,:],dataset[i]) # 计算第j个质心到第i个数据点的距离
                if dist_j_i<minDist:
                    minDist=dist_j_i
                    minIndex=j
            if cluster[i,0]!=minIndex:#如果第i个数据的分类变化了，则需要继续循环
            # 直到所有点的聚类结果不再变化
                cluster_changed = True
            cluster[i,:]=minIndex,minDist**2
        #print (centroids)
        # m个点的聚类结束之后，重新计算质心
        for centre_point in range(k):
            pts_in_cluster =dataset[nonzero(cluster[:,0].A==centre_point)[0]]
            # mat 将二维数组转换为矩阵  mat.A 将矩阵转换为数组类型（numpy 的narray）
            # 将每个数据的聚类结果转化为数组类型，然后选出当前分类的数据集索引
            # 从dataset中取出当前类别下的数据集
            centroids[centre_point,:]=mean(pts_in_cluster,axis=0) #按列求平均
    return centroids,cluster,count
    
def load_dataset(filename):
    dataMat=[]
    data_class=[]
    file = open(filename)
    labels=file.readline().strip().split(',')[1:]
    for line in file.readlines():
        current_line = line.strip().split(',')
        #flt_line = map(float,current_line[1:-1])
        flt_line = [float(i) for i in current_line[1:-1]]
        data_class.append(current_line[-1])
        dataMat.append(flt_line)
    return array(dataMat),labels,data_class
file=r"F:\k_means\iris.csv"
iris_data,iris_labels,iris_class=load_dataset(file)
# draw
import matplotlib.pyplot as plt
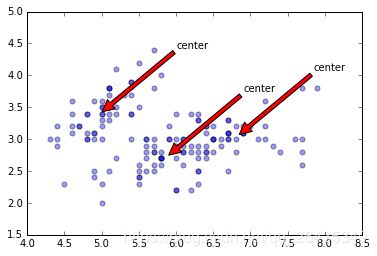
def draw(data,center):
    length=len(center)
    fig=plt.figure
    # 绘制原始数据的散点图
    plt.scatter(data[:,0],data[:,1],s=25,alpha=0.4)
    # 绘制簇的质心点
    for i in range(length):
        plt.annotate('center',xy=(center[i,0],center[i,1]),xytext=\
        (center[i,0]+1,center[i,1]+1),arrowprops=dict(facecolor='red'))
    plt.show()
# 为了克服K-Means算法收敛于局部最小值的问题，
# 提出了一种二分K-均值(bisecting K-means)
# 算法流程
"""
将所有的点看成是一个簇
当簇小于数目k时
    对于每一个簇
        计算总误差
        在给定的簇上进行K-均值聚类,k值为2
        计算将该簇划分成两个簇后总误差
    选择使得误差最小的那个簇进行划分
"""
# 二分k_means实现
def bi_k_means(dataset,k):
    m,n=shape(dataset)
    init_centroid = mean(dataset,axis=0).tolist() #初始化一个质心
    cluster=mat(zeros((m,2)))
    centroids=[]
    centroids.append(init_centroid)
    for i in range(m):
        cluster[i,1]=dist_eclud(init_centroid,dataset[i,:])**2 #计算初始sse     
    while len(centroids)<k:
        min_sse=inf
        # 寻找待分裂的质心
        for i in range(len(centroids)):
            # 对于目前的每个质心，计算是否要分裂
            # 对于当前类别的数据，计算二分后的SSE，对于各个质心，选择最小的SSE进行二分
            pst_to_split=dataset[nonzero(cluster[:,0].A==i)[0]]
            new_centroid,new_cluster,count=k_means(pst_to_split,2)
            split_sse=sum(new_cluster[:,1]) #分裂当前质心后的sse
            not_split_sse=sum(cluster[nonzero(cluster[:,0].A!=i)[0],1])#未分离质心的SSE
            if not_split_sse+split_sse<min_sse:
                min_sse=not_split_sse+split_sse
                best_split = i
                best_centroid = new_centroid
                best_cluster = new_cluster.copy()
        # 对于每个质心循环之后，找出了使得sse最小的分类质心
        # 修改并添加质心
        best_cluster[nonzero(best_cluster[:,0].A==0)[0],0]=best_split
        best_cluster[nonzero(best_cluster[:,0].A==1)[0],0]=best_split+1
        for class_index in range(best_split+1,len(centroids)):
            cluster[nonzero(cluster[:,0].A==class_index)[0],0]=class_index+1
        centroids[best_split]=best_centroid[0,:].tolist()[0]
        centroids.insert(best_split+1,best_centroid[1,:].tolist()[0])
        cluster[nonzero(cluster[:,0].A==best_split)[0],:]=best_cluster
    return mat(centroids),cluster
centroids,clusters,count=k_means(iris_data,3)
draw(iris_data,centroids)
bi_centroids,bi_clusters=bi_k_means(iris_data,3)
draw(iris_data,bi_centroids)