zzuli 第九届ACM校赛题解

题目链接：https://acm.zzuli.edu.cn/zzuliacm/contest.php?cid=1220

“玲珑杯”郑州轻工业学院第九届ACM程序设计大赛暨河南高校邀请赛-正式赛

Problem A: tmk射气球

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 575   Solved: 106

Submit Web Board

Description

有一天TMK在做一个飞艇环游世界，突然他发现有一个气球匀速沿直线飘过，tmk想起了他飞艇上有一把弓，他打算拿弓去射气球，为了提高射击的准确性，他首先在飞艇上找到一个离气球最近的一个点，然后射击（即使气球在飞船的正上方），现在求某些时刻飞艇上的点和气球的距离最小是多少（这个最小距离我们简称为飞艇到气球的距离）。

Input

第一行一个整数T(T<=20)，表示有T组测试数据

每组测试数据，有两行。

第一行有5个整数，h,x1,y1,x2,y2，其中h表示飞船的高度，飞船可抽象为一个线段，(x1,y1)(x2,y2)分别是这个线段的端点（有可能会有(x1,y1)(x2,y2)重合的情况）

第二行有6个整数，x,y,z,X,Y,Z分别表示气球的在第0秒的时候的横坐标，纵坐标，高度，一秒时间气球横坐标的变化量，一秒时间气球纵坐标的变化量，一秒时间气球高度的变化量(如果现在气球在(x0,y0,z0)下一秒坐标就为(x0+X,y0+Y,z0+Z))

第三行1个整数n，表示询问组数

接下来的n行，每行一个整数，表示询问的秒数t

题目涉及的整数除了T以外，范围均为[0,1000]

Output

每组询问输出n行，每行输出一个数，表示在t秒的时候飞艇与气球的距离最小是多少，保留两位小数

Sample Input

1

1 1 1 2 2

0 0 0 4 4 4 

2

0

3

Sample Output

1.73

17.92

HINT

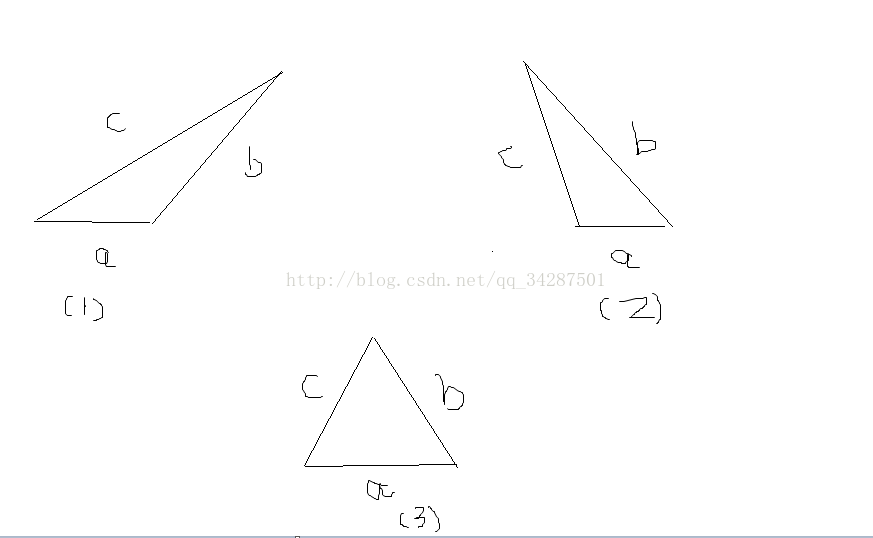
解析：三个点建一个三角形，然后如下图，一共就三种情况，a代表飞船，b、c代表飞船到气球的两条边，图1是线段右端点距离气球近（角C是钝角），输出b，图2是左端点距离近（角B是钝角），输出c，图3是输出h，下面分别模拟这三种情况就好，比较坑的是要用double，用int分开的每一个计算都要*1.0，不然WA

代码：

#include
#include
#include
#include
#include
#include
#include

Problem B: base64解密

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 348   Solved: 153

Submit Web Board

Description

码值	字符	码值	字符	码值	字符	码值	字符	码值	字符	码值	字符	码值	字符	码值	字符
0	A	8	I	16	Q	24	Y	32	g	40	o	48	w	56	4
1	B	9	J	17	R	25	Z	33	h	41	p	49	x	57	5
2	C	10	K	18	S	26	a	34	i	42	q	50	y	58	6
3	D	11	L	19	T	27	b	35	j	43	r	51	z	59	7
4	E	12	M	20	U	28	c	36	k	44	s	52	0	60	8
5	F	13	N	21	V	29	d	37	l	45	t	53	1	61	9
6	G	14	O	22	W	30	e	38	m	46	u	54	2	62	+
7	H	15	P	23	X	31	f	39	n	47	v	55	3	63	/

 　　Base64编码要求把3个8位字节（3*8=24）转化为4个6位的字节（4*6=24），之后在6位的前面补两个0，形成8位一个字节的形式。 如果剩下的字符不足3个字节，则用0填充，输出字符使用'='，因此编码后输出的文本末尾可能会出现1或2个'='。

为了保证所输出的编码位可读字符，Base64制定了一个编码表，以便进行统一转换。编码表的大小为2^6=64，这也是Base64名称的由来。

如对字符’0’进行Base64加密，则是如下步骤:

字符’0’的二进制为00110000，前六位拿出来，前面补两个0则是00001100，对应表得字符M。后面不足6位，只有两位0，拿出来，前面补6个0，则是00000000，对应表得字符A。

由于还有2个6位的字节没显示，则用两个=字符补充

那么字符0的Base64编码为MA==

现在蛋蛋给了你一段加密后的Base64密文，他说题意隐藏在密文里面，如果你知道了题意，就肯定可以做出本题。密文如下:

d2hhdCBpcyB0aGUgcmVtYWluZGVyIHdoZW4gdGhlIG51bWJlciBpcyBkaXZpZGVkIGJ5IDIwMTc/

Input

第一行一个整数t，代表有t组数据，每组数据输入一个整数x，0<=x<=2^31-1

Output

输出一个整数x，x为答案

Sample Input

3

0

1

2016

Sample Output

0

1

2016

HINT

解析：直接%2017

代码：

#include
#include
#include
#include
#include
#include
#include

Problem C: DOBRI

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 510   Solved: 174

Submit Web Board

Description

给出一个包含N个整数的序列A，定义这个序列A的前缀和数组为SUM数组 ，当SUM数组中的第i个元素等于在i前面的三个元素的和，那么第i个元素就称为GOOD。 那么这个SUM数组中包含多少个GOOD 元素?

Input

第一行整数T表示数据组数（1<=T<=10)

每组数据以下格式：

输入的第一行包含一个整数N (1<=N<=100000), 表示序列A的长度。

输入的第二行包含N个用空格隔开的整数，表示序列A (-100000<=Ai<=100000).

Output

每组数据输出仅一行，输出这个SUM数组中包含多少个GOOD元素。

Sample Input

3

4

1 1 1 3

4

1 2 3 10

6

5 -2 -3 1 3 3

Sample Output

1

0

1

HINT

解析：遍历一遍，记录前缀和数组sum[N] 前三个的和等于当前数的个数

代码：

#include
#include
#include
#include
#include
#include
#include

Problem D: hipercijevi

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 644   Solved: 122

Submit Web Board

Description

在遥远的星系， 最快的交通方式是用某种管道。 每个管道直接互相连接N个站。 那么我们从第一个站到第N个站最少要经过多少个站呢？

Input

输入文件的第一行为T表示有T组数据

每个数据第一行包含三个正整数 N (1<=N<=100000) 表示站的个数； K (1<=K<=1000) 表示一个管道直接连接了多少个站； M (1<=M<=1000) 表示管道的数量。

接下来的M行， 每行包含一个管道的描述： K个正整数， 表示这个管道连接的K个站的编号。

 

Output

输出文件T行，每行包含一个正整数，表示从第一个站到第N个站最少需要经过多少个站。 如果无法从第一个站到达第N个站，输出-1 。

Sample Input

2

9 3 5

1 2 3

1 4 5

3 6 7

5 6 7

6 8 9

15 8 4

11 12 8 14 13 6 10 7

1 5 8 12 13 6 2 4

10 15 4 5 9 8 14 12

11 12 14 3 5 6 1 13

Sample Output

4

3

HINT

解析：每条管道建立一个点，把管道中的所有点连一下，然后BFS一遍，结果  / 2 + 1（管道也算一个点了，所以要除2），如果mp[N][N] 10^10必然爆栈，这里用到链式前向星，由于数据比较多，需要要到输入挂，自己百度

代码：

#include
#include
#include
#include
#include
#include
#include
 q;
    q.push((P){1, 0});
    memset(vis, 0, sizeof(vis));
    vis[1] = 1;
    while(!q.empty())
    {
        P s = q.front(); q.pop();
        if(s.first == n) return s.second / 2 + 1;
        for(int i = head[s.first]; i != -1; i = p[i].nxt)
        {
            if(vis[p[i].to]) continue;
            vis[p[i].to] = 1;
            q.push((P){p[i].to, s.second + 1});
        }
    }
    return -1;
}


inline void q_read(int &num)
{
    int f = 1;
    char ch;
    while(true)
    {
        ch = getchar();
        if(ch == '-') f = -1;
        if(isdigit(ch))
        {
            num = ch - '0';
            break;
        }
    }
    while(ch = getchar(), isdigit(ch)) num = num*10 + ch - '0';
    num *= f;
}


int main()
{
    int t, k, m, from, to;
    q_read(t);
    while(t--)
    {
        memset(head, -1, sizeof(head));
        cnt = 0;
        q_read(n); q_read(k); q_read(m);
        for(int i = 1; i <= m; i++)
        {
            from = n + i;
            for(int j = 1; j <= k; j++)
            {
                q_read(to);
                add(from, to);
                add(to, from);
            }
        }
        printf("%d\n", bfs());
    }
    return 0;
}

Problem E: Can Win

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 335   Solved: 42

Submit Web Board

Description

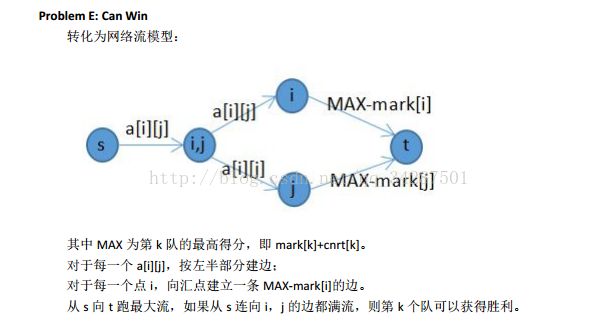
Zhc很喜欢看某个竞技比赛，比赛的规则是这样的：队伍分成AB两组进行比赛，除了组内比赛，两组之间还会进行一定的比赛，每场比赛赢者得1分，输者不得分，没有平局的情况。 在A组里面Zhc有一支自己非常喜欢的队伍，现在比赛已经进行到一半了，Zhc想知道，他支持的那支队伍有没有可能获得最终的胜利（A组最高分即为胜利，允许多支队伍同时最高分）

 

Input

 第一行输入样例组数T<=110

每组样例第一行输入A组队伍数量n<=400，以及Zhc支持的队伍编号（1-n）K<=n

第二行按编号输入A组各队伍目前的成绩Mark[i]<= 300000

第三行按编号输入A组各队伍剩余比赛总场数Cnt[i]<= 300000

下面有一个N*N的矩阵，其中A[i][j]代表编号i的队伍跟编号j的队伍剩余比赛场数A[i][j]<=100

 

Output

 对每组样例输出”Yes”或者”No”（不用输出引号）代表Zhc支持的队伍能获得最终的胜利，换行处理

 

Sample Input

1

2 1

5 6

2 2

0 1

1 0

Sample Output

Yes

解析：

代码：

#include
#define M 2000009
#define N 160010
#define maxn 409
using namespace std;
const int INF = 0x3f3f3f3f;

int n, kk;
int win[maxn], fight[maxn][maxn], Max;


inline void q_read(int &num)
{
    int f = 1;
    char ch;
    while(true)
    {
        ch = getchar();
        if(ch == '-') f = -1;
        if(isdigit(ch))
        {
            num = ch - '0';
            break;
        }
    }
    while(ch = getchar(), isdigit(ch)) num = num * 10 + ch - '0';
    num *= f;
}



struct Edge{
    int u, v, cap, flow, next;
}E[M];

struct Dinic{
    int head[N], d[N], iter[N];
    int tot, sink, source;

    void init() {
        memset(head, -1, sizeof(head));
        tot = 0;
    }

    inline void AddEdge(int u, int v, int cap) {
        E[tot].u = u; E[tot].v = v; E[tot].cap = cap; E[tot].flow = 0; E[tot].next = head[u]; head[u] = tot++;
        u = u ^ v; v = u ^ v; u = u ^ v;
        E[tot].u = u; E[tot].v = v; E[tot].cap = 0; E[tot].flow = 0; E[tot].next = head[u]; head[u] = tot++;
    }

    inline bool bfs(int s) {
        int u, v;
        memset(d, 0, sizeof(d));
        queue Q;
        Q.push(s);
        d[s] = 1;
        while (!Q.empty()) {
            u = Q.front(); Q.pop();
            if (u == sink) return true;
            for (int i = head[u]; ~i; i = E[i].next) {
                v = E[i].v;
                if (!d[v] && E[i].cap - E[i].flow > 0) {
                    d[v] = d[u] + 1;
                    Q.push(v);
                }
            }
        }
        return false;
    }

    int dfs(int x, int a) {
        if (x == sink || a == 0)
            return a;
        int f, flow = 0;
        for (int i = head[x]; ~i; i = E[i].next) {
            int v = E[i].v;
            if (d[v] == d[x] + 1 && E[i].cap - E[i].flow > 0) {
                f = dfs(v, min(a, E[i].cap - E[i].flow));
                E[i].flow += f;
                E[i^1].flow -= f;
                flow += f;
                a -= f;
                if (!a) break;
            }
        }
        if (flow == 0) d[x] = 0;
        return flow;
    }

    int Maxflow(int source, int sink) {
        int flow = 0;
        this->sink = sink;
        //memcpy(iter, head, sizeof head);
        while (bfs(source)) flow += dfs(source, INF);
        return flow;
    }
}dinic;


int init() {
    //scanf("%d %d", &n, &kk);
    q_read(n); q_read(kk);
    Max = -INF;
    int t;
    for (int i = 1; i <= n; i++) {
        //scanf("%d", &win[i]);
        q_read(win[i]);
        Max = max(Max, win[i]);
    }
    int total = win[kk];
    for(int i = 1; i <= n; i++)
    {

        //scanf("%d", &t);
        q_read(t);
        if(i == kk) total += t;
    }

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            //scanf("%d", &fight[i][j]);
            q_read(fight[i][j]);
        }
    return total;
}

void solve(int total) {
    //bool flag = false;
    int source = 0, sink =  N - 1, cnt;

    if (total < Max)
    {
        puts("No");
        return ;
    }

    cnt = n + 1;
    dinic.init();
    int Sum = 0;
    for (int j = 1; j <= n; j++)
    {
        if(j == kk) continue;
        dinic.AddEdge(j, sink, total - win[j]);
        for (int k = j + 1; k <= n; k++)
        {
            if (k == kk) continue;
            dinic.AddEdge(source, cnt, fight[j][k]);
            Sum += fight[j][k];
            dinic.AddEdge(cnt, j, fight[j][k]);
            dinic.AddEdge(cnt++, k, fight[j][k]);
        }
    }
    int MaxFlow = dinic.Maxflow(source, sink);
    if (MaxFlow == Sum) puts("Yes");
    else puts("No");

}

int main() {
    int test;
    scanf("%d", &test);
    while (test--) {
        int total = init();
        solve(total);
    }
    return 0;
}

Problem F: Tmk吃汤饭

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 451   Solved: 193

Submit Web Board

Description

Tmk喜欢吃汤饭！

Tmk喜欢吃汤饭！！

Tmk喜欢吃汤饭！！！

汤饭窗口分点餐和取餐两个窗口，一位蜀黍负责点餐窗口，一位蜀黍负责煮汤，一位蜀黍负责打饭，点餐需要1个单位时间，每一份需要煮5个单位时间，同一时间最多可以煮4份。

现在tmk要考考你，给你所有人的到达时刻，每个人在到达时刻排到点餐队列的末尾，点完餐后排到取餐队列，煮好后即可取餐，问你最后一个人取到汤饭的时间。

除了点餐和煮汤的时间，其他时间忽略不计，没人插队，而且他们意志坚定，所以不会中途而废,每个汤饭必须连续煮，不能中断。

 

Input

第一行一个T(0

对于每组数据：

第一行一个整数n(0<=n<=100000)表示有n个人。

第二行，n个整数，以空格隔开(其中t[i]>=0 && t[i] < 50000000 && t[i] > t[i-1])，t[i]表示第i个人的到达时刻。

 

Output

对于每个样例，输出最后一个人取到汤饭的时间。

 

Sample Input

2

3

4 5 6

5

2 3 4 5 6

Sample Output

12

13

HINT

解析：用队列一直模拟，队列中如果>=4需要把最前面的出队，然后如果后面还有人，取max(该人到来时间+1,队列最小值+5)入队，一直模拟即可

代码：

#include
#include
#include
#include
#include
#include
#include

Problem G: 密室逃脱

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 296   Solved: 48

Submit Web Board

Description

XOR在玩密室逃脱，在某一关中，桌上有一个一张纸，上面写着“请根据所给例子求解答案从而获得密码”，下面写了几个字符串“01 10 11”，而答案为“6”，聪明的XOR立马就知道了这是给出一些二进制数字S，求存在多少对有序二元组（i,j）使得S[i]^S[j]

 

Input

第一行一个整数T，表示数据组数。

对于每组数据，首先读入两个整数n,m（n*m<=1000000），接下来为n行，每行为一个长度为m的01串，表示一个二进制数字

 

Output

对于每个数据，输出一个整数x，表示二元组数目

 

Sample Input

1

3 2

01

10

11

Sample Output

6

HINT

解析：可以发现 a^b 与 a 的大小只与 b 的二进制表示中最高位的 1 所在的那一位有关，如果 a 在
这一位是 0，a^b>a，否则 a^b 个数的最高位 1 是这一位，将它们相乘后累加即可，时间复杂度为 O(n*m+m)

代码：

#include
#include
#include
#include
#include
#include
#include

Problem H: 维克兹的进制转换

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 231   Solved: 48

Submit Web Board

Description

我进入了突如其来的强光。闪烁。闪烁，闪烁，闪烁。我调整好眼睛，评估我前方的景观。

有东西在乱窜。我往下看，发现了一只小个的白色生物，用后腿站立着，嗅闻着我的躯体。它吸引了我的注意。

你有什么用途？

我分析这个生物。品红色热能光束一闪而过，它曾颤动的地方扬起尘埃。

哺乳动物...夜行习性...无可挑剔的听觉。难以置信的弱小。但它们的繁殖能力如此强大。

“唔，”我喃喃自语。希望能发现更加复杂的物体；那些东西把我给迷住了。

消化并学习：这是我的目的。和我一起旅行的其它来客都很原始：杀死并吃掉，杀死并吃掉。我需要收集所有可用的信息——收获更多有价值的资源。

维克兹是少数热爱学习的虚空来客之一，他带着非凡的意图探索着符文之地：吸收掉所有知识。凭借着他不断地注视，维克兹可以发射瓦解光线来灭除并分析他途中的一切东西，并为他供给数量庞大的信息。没人知道他为什么需要如此多的材料，尽管有人推测他设法了解符文之地，是为了加速它的毁灭。

有一天，维克兹突发奇想，他觉得古老的二进制魔法串太过单一，于是他规定二进制除了 0 和 1，还有 2。现在维克兹想知道该规则下十进制数 N 转换为二进制数的方案数，维克兹当然可以轻松算出来，但他正好缺一个一起游览符文大地的伙伴，于是他把这个问题交给了你，希望你不要让他失望才好。

 

Input

输入包括 T 组数据，每组数据有一个非负整数 N。（T <= 1e5, N <= 1e7）

 

Output

输出一个正整数代表十进制数 N 转换为二进制数的方案数。

 

Sample Input

4

1

2

3

4

Sample Output

1

2

1

3

HINT

1 ——> 1
2 ——> 10 or 2
3 ——> 11
4 ——> 100 or 20 or 12

解析：对于一个数，我们先考虑其最后一位为 0、1、2 中的哪一个。如果 n&1，那么最后一位只能是 1，所以 f[n] = f[n/2]。否则，那么最后一位可以是 0 或则 2，所以 f[n]=f[n/2]+f[n/2-1]。特殊地，f[0] = 1，f[1] = 1，f[2] = 2。

代码：

#include
#include
#include
#include
#include
#include
#include

Problem I: 这里是天堂！

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 864   Solved: 96

Submit Web Board

Description

Maple他打代码打累了，于是Maple跑去找猫猫们来拯救自己。

Maple来到了一个空房间里，房间的隔壁是一个有很多只猫猫的房间，在Maple的房间里有一个按钮，每次按一下按钮，就会有且只有一只猫猫从旁边的房间里跑过来找Maple玩，当然当隔壁房间没有猫的时候并不会有猫猫跑过来。

Maple按了几次按钮后发现跑过来的猫猫只有白色和黄色两种毛色，而且如果假设当每次按按钮后旁边房间剩下的猫跑过来的概率都相同，那么Maple就开始想，如果当隔壁房间共有n只白猫和m只黄猫时，当他按了k次按钮后，跑过来的白猫数量和黄猫数量分别为a只和b只的概率是多少。

 

Input

第一行有一个整数T，代表有T组数据(1<=T<=2000)

每组数据有五个整数n,m,k,a,b，其中0<=n,m,k,a,b<=10

 

Output

对于每组数据，得到的概率为一个分数A/B（A<=B且AB为互质整数），输出两个整数A、B，用一个空格分开。

 

Sample Input

2

1 1 1 1 0

9 1 10 9 1

Sample Output

1 2

1 1

HINT

特殊的，概率为0的分数表示法为0/1。

解析：比赛一直过不了0 1、 1 1这两个特殊情况，就算最后给过了，爆int没发现，以为公式错了，就没再写，还是自己太菜，，，

代码：

#include
#include
#include
#include
#include
#include
#include