Coursera机器学习基石笔记week9
Linear Regression
线性回归的预测函数取值在整个实数空间,这跟线性分类不同。 h ( x ) = w T X h(x)=w^TX h(x)=wTX
在一维或者多维空间里,线性回归的目标是找到一条直线(对应一维)、一个平面(对应二维)或者更高维的超平面,使样本集中的点更接近它,也就是残留误差Residuals最小化。如下图所示:

一般最常用的错误测量方式是基于最小二乘法(这里是线性的),其目标是计算误差的最小平方和对应的权重w,即上节课介绍的squared error:

Linear Regression Algorithm
首先,运用矩阵转换的思想,将EinEin计算转换为矩阵的形式。
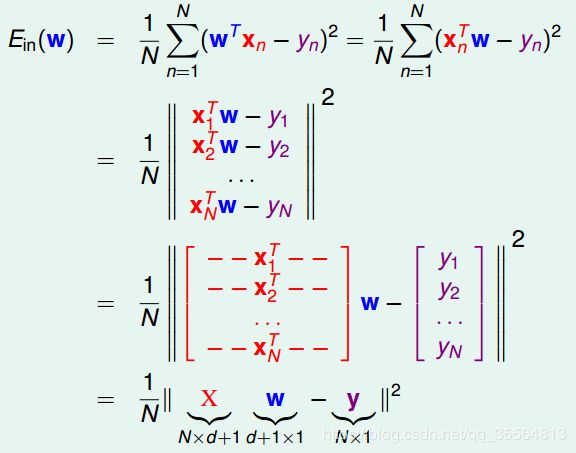
对于此类线性回归问题, E i n ( w ) E_{in}(w) Ein(w)一般是个凸函数。凸函数的话,我们只要找到一阶导数等于零的位置,就找到了最优解。那么,我们将 E w E_w Ew对每个 w i w_i wi,i=0,1,⋯,d求偏导,偏导为零的 w i w_i wi,即为最优化的权重值分布。

那么如何求导呢?

让倒数为0,即可计算出w:

对于可逆的矩阵 X T X X^TX XTX来说,我们就可以使用上述伪逆矩阵进行计算了,但是针对于奇异(不可逆)矩阵来说,逆矩阵 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1就不一定存在了。但是一般来说,如果样本数量N远大于样本维度d+1的话,是能保证矩阵的逆是存在的。如果不可逆,大部分计算软件也可以处理这个问题,计算出一个逆矩阵。所以,一般的伪逆矩阵都是可解的。
Generalization Issue

有两种观点:1、这不属于机器学习范畴。因为这种closed-form解的形式跟一般的机器学习算法不一样,而且在计算最小化误差的过程中没有用到迭代。2、这属于机器学习范畴。因为从结果上看,EinEin和EoutEout都实现了最小化,而且实际上在计算逆矩阵的过程中,也用到了迭代。

那么 E i n ( w L I N ) = 1 N ∣ ∣ ( I − X X + ) y ∣ ∣ 2 = 1 N ∣ ∣ ( I − H ) y ∣ ∣ 2 E_in(w_{LIN})=\frac{1}{N}||(I-XX^+)y||^2=\frac{1}{N}||(I-H)y||^2 Ein(wLIN)=N1∣∣(I−XX+)y∣∣2=N1∣∣(I−H)y∣∣2

-
粉色区域是X分别乘以不同的w来生成一个新的空间,那么我们ŷ也是由w乘以X产生的,因此ŷ要在这个空间内。
-
我们要做的就是让y与ŷ最小,也就是垂直于这个空间的时候。
-
H就是把y映射为ŷ,Hy=ŷ
-
I-H就是通过(I−H)y=y−ŷ,使y转换为y−ŷ
接下来,先探究一下H的性质:
H a t M a t r i x H = X ( X T X ) − 1 X T Hat \ Matrix\ H=X(X^TX)^{-1}X^T Hat Matrix H=X(XTX)−1XT
-
对称性(symetric),即H= H T H^T HT:
H T = ( X ( X T X ) − 1 X T ) T H^T=(X(X^TX)^{-1}X^T)^T HT=(X(XTX)−1XT)T
= X ( ( X T X ) − 1 ) T X T =X((X^TX)^{-1})^TX^T =X((XTX)−1)TXT
= X ( X T X ) − 1 X T =X(X^TX)^{-1}X^T =X(XTX)−1XT
= H =H =H
-
幂等性(idempotent),即 H 2 = H H^2=H H2=H:
H 2 = ( X ( X T X ) − 1 X T ) ( X ( X T X ) − 1 X T ) H^2=(X(X^TX)^{-1}X^T)(X(X^TX)^{-1}X^T) H2=(X(XTX)−1XT)(X(XTX)−1XT)
= X ( X T X ) − 1 ( X T X ) ( X T X ) − 1 X T =X(X^TX)^{-1}(X^TX)(X^TX)^{-1}X^T =X(XTX)−1(XTX)(XTX)−1XT
= X ( X T X ) − 1 X T =X(X^TX)^{-1}X^T =X(XTX)−1XT
= H =H =H
首先复习一下迹运算。
-
如果A是m ∗ * ∗n,B是n ∗ * ∗m的话,那么trace(AB)=trace(BA)
-
多个矩阵相乘得到的方阵的迹,和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的。当然,我们需要考虑挪动之后矩阵乘积依然定义良好:
Tr(ABC)=Tr(CAB)=Tr(BCA)
-
如果C和D都是m ∗ * ∗m的,那么trace(C+D)=trace©+trace(D)
-
如果 α \alpha α是一个标量的话,那么 t r a c e ( α C ) = α t r a c e ( C ) trace(\alpha C)=\alpha trace(C) trace(αC)=αtrace(C), t r a c e ( α ) = α trace(\alpha)=\alpha trace(α)=α
这里给出trace(I-H)=N-(d+1),那么为什么呢?一个矩阵的trace(迹)等于其对角元素的和。
t r a c e ( I − H ) = t r a c e ( I ) − t r a c e ( H ) trace(I-H)=trace(I)-trace(H) trace(I−H)=trace(I)−trace(H)
= N − t r a c e ( X X + ) = N − t r a c e ( X ( X T X ) − 1 X T ) =N-trace(XX^+)=N-trace(X(X^TX)^{-1}X^T) =N−trace(XX+)=N−trace(X(XTX)−1XT)
= N − t r a c e ( ( X T X ) ( X T X ) − 1 ) =N-trace((X^TX)(X^TX)^{-1}) =N−trace((XTX)(XTX)−1)
= N − I d + 1 =N-I_{d+1} =N−Id+1
= N − ( d + 1 ) =N-(d+1) =N−(d+1)
从上图可知,y=f(x)+noise。之前我们提到H作用于某个向量可以得倒在span上的投影,而I-H作用于某个向量,那么可以得到与span垂直的向量,也就是图里的y−ŷ ,那么也就是说
(I-H)noise=y−ŷ 。
这个y−ŷ 是真实值与预测值的差,其长度就是所有点的平方误差之和。于是可以知道:
要得到结论,我们需要先了解一下相关概念:
由上述可知,H是对称的,又因为I是对称的,那么 I − H = ( I − H ) T I-H=(I-H)^T I−H=(I−H)T
H是幂等的,那么 H 2 = H H^2=H H2=H, ( I − H ) 2 = I 2 − 2 H ∗ I + H 2 = I − 2 H + H = I − H (I-H)^2=I^2-2H*I+H^2=I-2H+H=I-H (I−H)2=I2−2H∗I+H2=I−2H+H=I−H
E i n ( W L I N ) = 1 N ∣ ∣ y − y ^ ∣ ∣ 2 E_{in}(W_{LIN})=\frac{1}{N}||y−ŷ ||^2 Ein(WLIN)=N1∣∣y−y^∣∣2
= 1 N ∣ ∣ ( I − H ) n o i s e ∣ ∣ 2 =\frac{1}{N}||(I-H)noise||^2 =N1∣∣(I−H)noise∣∣2
= 1 N t r a c e ( ( I − H ) T ( I − H ) n o i s e ∗ n o i s e T ) =\frac{1}{N}trace((I-H)^T(I-H)noise*noise^T) =N1trace((I−H)T(I−H)noise∗noiseT)
= 1 N t r a c e ( ( I − H ) 2 n o i s e ∗ n o i s e T ) =\frac{1}{N}trace((I-H)^2noise*noise^T ) =N1trace((I−H)2noise∗noiseT)
= 1 N t r a c e ( ( I − H ) n o i s e ∗ n o i s e T ) =\frac{1}{N}trace((I-H)noise*noise^T ) =N1trace((I−H)noise∗noiseT)
≤ 1 N t r a c e ( I − H ) ∣ ∣ n o i s e ∣ ∣ 2 \leq\frac{1}{N}trace(I-H)||noise||^2 ≤N1trace(I−H)∣∣noise∣∣2
≤ 1 N ( N − ( d + 1 ) ) ∣ ∣ n o i s e ∣ ∣ 2 \leq\frac{1}{N}(N-(d+1))||noise||^2 ≤N1(N−(d+1))∣∣noise∣∣2
那么可以知道: E ˉ i n \bar{E}_{in} Eˉin= n o i s e l e v e l ∗ ( 1 − d + 1 N ) noise\ level * (1-\frac{d+1}{N}) noise level∗(1−Nd+1)
那么直觉上可以得出,当在训练集往一些特定的noise偏过去的时候,那么在测试集中,对于其他训练集上没有的噪音就会使测试集的偏差往反方向生成。
E ˉ o u t \bar{E}_{out} Eˉout= n o i s e l e v e l ∗ ( 1 + d + 1 N ) noise\ level *(1+\frac{d+1}{N}) noise level∗(1+Nd+1)

Linear Regression for Binary Classfication

从上图可以看出, e r r 0 / 1 ≤ e r r s q r err_{0/1}\leq err_{sqr} err0/1≤errsqr
那么根据之前vc bound的知识点,我们可以得出:

从图中可以看出,用 e r r s q r err_{sqr} errsqr代替 e r r 0 / 1 err_{0/1} err0/1, E o u t E_{out} Eout仍然有上界,只不过是上界变得宽松了。也就是说用线性回归方法仍然可以解决线性分类问题,效果不会太差。二元分类问题得到了一个更宽松的上界,但是也是一种更有效率的求解方式。
总结
本节课,我们主要介绍了Linear Regression。首先,我们从问题出发,想要找到一条直线拟合实际数据值;然后,我们利用最小二乘法,用解析形式推导了权重w的closed-form解;接着,用图形的形式得到 E o u t − E i n ≈ 2 ( N + 1 ) N E_{out}−E_{in}≈\frac{2(N+1)}{N} Eout−Ein≈N2(N+1),证明了linear regression是可以进行机器学习的;最后,我们证明linear regressin这种方法可以用在binary classification上,虽然上界变宽松了,但是仍然能得到不错的学习方法。

