手写的线性回归实例（代码仔细讲解）

根据链家网上的数据，自己写了两个程序，预测一下房价

对代码的讲解是比较详细的，恳请耐心阅读代码，如果你对线性回归基础还不是很了解，完全可以看我的代码理解

注释全部在代码中

 第一个例子：使用 y = k*x + b 这样一个简单模型

# 自己手写的线性回归实例   author:杨博文
# 例子说明，根据链家网站提供的房屋数据，训练出预测模型
# 使用的是深圳的房屋价格  网址：https://sz.fang.lianjia.com/loupan/
# 已经选取了部分数据在下面，可以直接使用
import numpy as np
import matplotlib.pyplot as plt

# --------------最简单的模型------------------
# 使用 y = k*x + b , 即 price = k*area + b

area = [79, 106, 177, 117, 600, 119, 67, 140, 100, 140, 88, 191]
price = [367, 230, 1350, 520, 5000, 880, 467, 1830, 800, 540, 650, 1719]  # 单位：万
# test data
area_test = [155,185,126,116,380,143,238]
price_test = [640,2700,240,590,1714.5,700,530]

# -------------------------------------------


if __name__ == '__main__':
    # 初始化
    k = 0
    b = 0
    lr = 1e-7 # learning rate
    iteration_times = int(1e5) # 梯度下降迭代次数，也就是循环次数

    # Loss(k,b) = ∑ ( yi - ( b + k*xi ) )^2  损失函数是对所有数据偏差平方的和
    # 要想找到合适的k和b ，使得Loss足够小，则需要不断修改k和b的值，使得Loss慢慢变小，也就是梯度下降
    # 注意，Loss函数里面k和b是变量了，应当理解成x，  而xi，yi反而是已知数据，它们是常量

    for i in range(iteration_times):
        k_gradient = 0
        b_gradient = 0
        # 每一次梯度下降的任务就是更新k和b，更新k和b需要对Loss求偏导

        # 这一步是求出Loss对k和b的偏导，因为Loss函数是求和，所以求出的偏导也是求和
        for j in range(len(area)):                      # Loss(k,b) = ∑ ( yi - k*xi - b )^2 这里化简了一下
            k_gradient += 2*(price[j]-k*area[j]-b)*(-area[j])  # Loss函数对k求偏导,然后累加，这里要仔细想想用哪一些值，
            b_gradient += 2*(price[j]-k*area[j]-b)*(-1)        # 求偏导都不会的话，还是先去看看高数吧

        # 求出偏导之后，即可下降，修改k和b的值
        k -= lr*k_gradient
        b -= lr*b_gradient

    # 经过上面的迭代，我们就找到合适的k和b，使得loss比较小啦，下面就可以看看结果了

    print(f"k的值:{k},b的值:{b}")
    print(f"预测的模型 y = {k}*x + {b}")
    # 先生成点，然后画图看结果
    x = np.linspace(50,500,100) # x代表房屋面积，从50到500，取100个点
    y = k*x+b   #根据x计算y
    plt.rcParams['font.sans-serif'] = ['SimHei']    # 用来正常显示中文标签，解决文字不能显示问题
    plt.plot(x,y,label="我们预测的直线")
    plt.legend()

    plt.plot(area,price,"ro",label="使用数据的点")
    plt.legend()

    plt.plot(area_test,price_test,"ko",label="测试的点")
    plt.legend()

    plt.show()

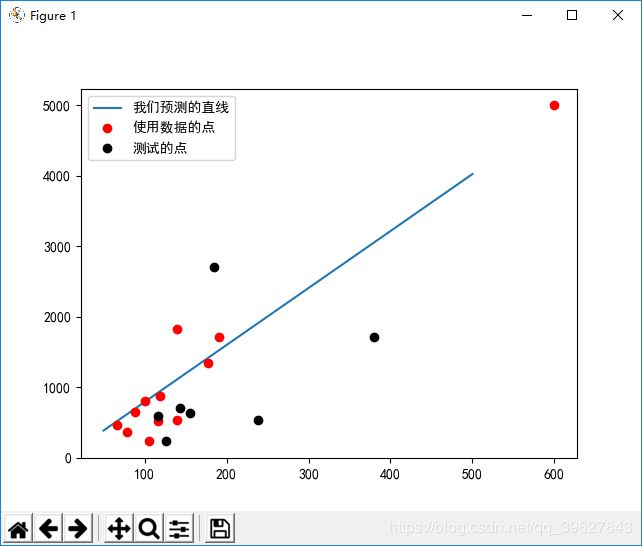
那么，运行上述代码，我们看到结果如下：

 

根据 画出的图像看出结果不是很准确，这是因为我们只考虑了房屋面积这一个因素，所以我决定再做一个更准确一点的，考虑更多因素