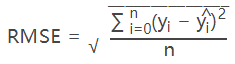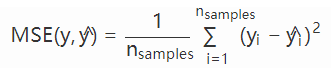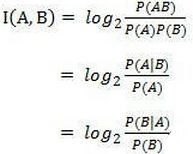1.训练集测试集划分方案
a)留出法hold-out
直接将原始数据集D划分为两个互斥集合,其中一个作为训练集S,另外一个作为测试集T,其中D=S并T,S交T=空。在划分的过程中应该尽量保持数据分布一致,即S,T的分布要和原始数据集一致,如原始数据集中正负样本比例为1:5,那么在S和T中正负样本比也应该为1:5。一般采用分层抽样的方案,即从正样本中抽取1份做训练集的正样本,从负样本中抽取1份做训练集的负样本。
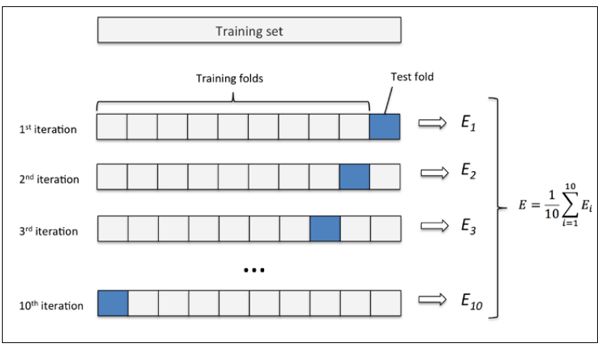
b)交叉验证法cross-validation
将原始数据集通过分层抽样划分为k个大小一致的互斥子集。然后,每次利用k-1各子集合的并集作为训练集,剩下的那个做测试集。这样就可以得到k个训练集/测试集的组合,从而可以进行k次训练和测试,最终返回的结果为k次测试结果的均值。
c)自助法bootstrapping
原始数据集包含m个样本,则有放回的抽样m次,组成一个包含m个样本的训练集D`,一个样本经过m次抽样任然没有被抽取到的概率为(1-1/m)**m=0.368,我们将D`作为训练集D-D`作为测试集,这样我们训练集和原始数据集一样有m个样本,同时测试集约有1/3的样本是训练集中没有出现过的。自助法在数据集较小、难以有效划分训练集/测试集时很有效;自助法能产生多个不同的训练集这对集成学习算法很有帮助;自助法改变了原始数据集的分布,因此在数据量足够的情况下,我们一般采用留出法和交叉验证法。
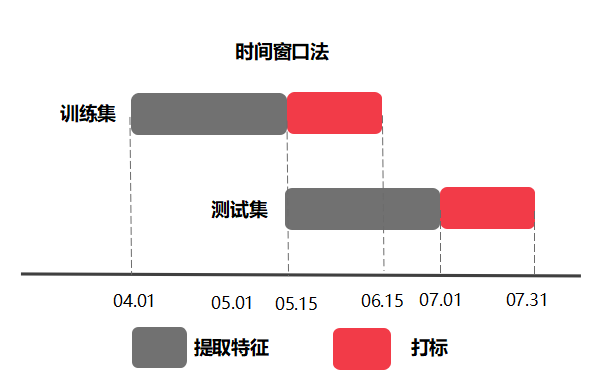
d)时间窗口划分法
在实际问题中,我们的做法一般是根据历史数据去预测未来某段时间发生的事情,在这种情况下,基于时间窗口的训练集测试集划分方案就很有用。我们根据线上线下一致性原则,将用户的历史数据按照时间窗口划分,例如选取4月到5月的数据为训练集,5月到6月的数据为测试集。一般在划分时分为标签窗口用于对待考察样本打标签,特征提取窗口用于对待考察样本提取特征。时间窗口划分法中的两个主要概念为窗口时间粒度的大小和窗口滑动的范围,粒度大小指包含了多少天,滑动的范围指从哪一天到哪一天。
2.偏差bias与方差variance
我们前面说过模型其实就是一个有x到y的函数映射f,我们通过已有数据训练得到这个映射f。偏差用于表征模型准不准,高偏差意味着模型精度较低;方差用于描述模型稳不稳,高方差意味着模型过拟合了。
偏差:描述的是预测值(估计值)的期望与真实值之间的差距。偏差越大,越偏离真实数据,如左图第二行所示。
方差:描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散,如左图右列所示。
3.评估指标
a)分类问题
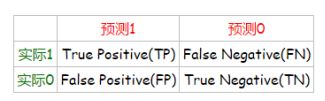
i.混淆矩阵
ii.准确率、精确度、召回率
准确率accuracy =预测正确的样本数目(包括正负样本)/提交样本数目
精确度precision =提交结果中正确的正样本数目/提交结果总数
TP/(TP+FP)
召回率recall =提交结果中正确正样本数据/实际数目
TP/(TP+FN)
iii.F1-SCORE
F1-SCORE主要用于不平衡分类,若是正负样本比例悬殊,如正样本占了90%,这个时候若你的模型将所有样本全预测为正样本,模型的精确度任然有0.9,但显然你的模型是一个很差的模型(一个负样本都没有预测出来),反之召回率在正负样本不均衡时也会存在这个问题,此时我们利用F1-SCORE来均衡的表征模型精度。
F1-SCORE = precision*recall*2/(precision+recall)
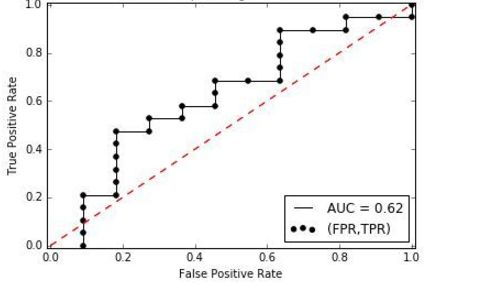
iv.ROC、AUC
ROC曲线
横坐标:FPR =实际为0预测为1/实际为0
纵坐标:TPR =实际为1预测为1/实际为1
其计算方法为将预测结果按照概率由小到大排序,然后依次往后移动下标,当出现一个正样本往y轴走1/正样本个数,出现一个负样本往x轴走1/负样本个数。
所以ROC曲线必过(0 , 0)和(1 , 1)。
AUC为ROC曲线下面积,AUC就是从所有1样本中随机选取一个样本,从所有0样本中随机选取一个样本,然后根据你的分类器对两个随机样本进行预测,把1样本预测为1的概率为p1,把0样本预测为1的概率为p0,p1>p0的概率就等于AUC。所以AUC反应的是分类器对样本的排序能力。根据这个解释,如果我们完全随机的对样本分类,那么AUC应该接近0.5。另外值得注意的是,AUC对样本类别是否均衡并不敏感,这也是不均衡样本通常用AUC评价分类器性能的一个原因。
AUC=((所有的正样本rank相加)-T*(T+1)/2)/(T*F)
T表示正样本数目,F表示负样本数目,对于概率一样的样本需均分排名
根据返回的AUC计算正样本个数:
1.将分类器分类结果由小按大排序,可完全确定为正样本的赋值为0.9,其余赋值为0.1。
2.假设0.9的样本个数为m个,则这一部分排名和为n+(n-1)+...+(n-m+1)
3.为0.1这一部分中正样本的排名和为[1+2+...+(n-m)]/(n-m)*(T-m)
4.根据AUC计算公式可得T
b)回归问题
i.平方根误差RMSE:预测值与真实值插值平方和的均值开方
ii.平均绝对误差MAE:预测值与真实值误差绝对值的均值
iii.平均平方误差MSE:预测值与真实值插值平方和的均值
c)聚类问题
i.兰德系数:需要给定实际类别信息C,假设K是聚类结果,a表示在C与K中都是同类别的元素对数,b表示在C与K中都是不同类别的元素对数,取值为[0 , 1]值越大越好
ii.互信息:是用来衡量两个数据分布的吻合程度。也是一有用的信息度量,它是指两个事件集合之间的相关性,取值为[0 , 1]越大越好
iii.轮廓系数(类内距离/类间距离):适用于实际类别信息未知的情况。对于单个样本,设a是与它同类别中其他样本的平均距离,b是与它距离最近不同类别中样本的平均距离,轮廓系数为,取值为[-1 , 1],同类别样本距离越相近且不同类别样本距离越远得分越高