双指针算法（持续更新）

双指针算法（Two Pointers）

算法思想： 利用问题本身与序列的特性（序列递增性质），使用两个下标i、j对序列进行扫描 （可以同向扫描，也可以反向扫描） ，以较低的复杂度解决问题。

TIPS：要注意双指针的方向选择！！！

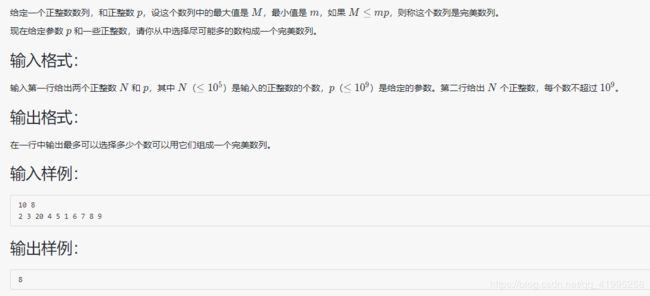
eg1. 给定一个递增的正整数序列和一个正整数M，求序列中不同位置的数a和b，是的它们的和恰好为M，输出所有满足条件的方案。

// 两个指针反向扫描
while(i < j)
{
	if(a[i]+a[j] == M)
	{
		printf("%d %d\n", i, j);
		i++; // 如果只需要第一个解，直接break即可。
		j--;
	}
	else if(a[i]+a[j] < M)
	{
		i++;
	}
	else 
	{
		j--;
	}
}

eg2. 序列合并问题

// 两个指针同向扫描
int merge(int A[], int B[], int C[], int n, int m)
{
	int i = 0, j = 0, index = 0;
	while(i<n && j<m)
	{
		if(A[i] <= B[j]) 
		{
			C[index++] = A[i++];
		}
		else 
		{
			C[index++] = B[j++];
		}
	}
	while(i < n)
	{
		C[index++] = A[i++];
	}
	while(j < m)
	{
		C[index++] = B[j++];
	}
	return index; // 返回序列C的长度 
}

eg3. PAT B1030 完美数列

思路分析：

本题可以用二分法，也可以使用双指针算法。

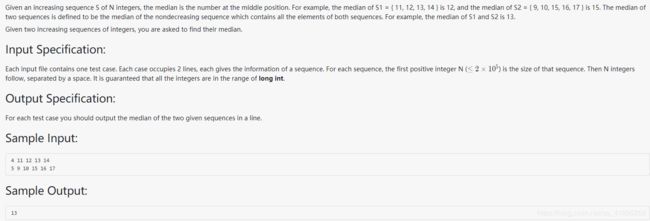
双指针算法： 当m1较小时，与其对应的M1也相对较小；当m2较大时，与其对应的M2也相对较大。即m1

代码（AC）：

#include 
#include 
#include 
using namespace std;

const int maxn = 100010;
int a[maxn];

int main()
{
	int n, p;
	scanf("%d %d", &n, &p);
	for(int i=0; i<n; i++)
	{
		scanf("%d", &a[i]);
	}
	sort(a, a+n);
	int i = 0, j = 0; // 利用同向双指针
	int ans = 0;
	while(i<n && j<n)
	{
		while(j<n && a[j]<=(long long)a[i]*p)
		{
			ans = max(ans, j-i+1); // 不断更新最大元素数
			j++; // 上一个i对应的j满足，则下一轮i+1也一定成立
		}
		i++;
	}
	printf("%d\n", ans);
	
	return 0;	
}  

eg.4 PAT A1029 Median

思路分析：

仿照数组合并的思路，但此处不需要真的将合并数组存下来，只需要利用i、j两个指针的移动，移到中值所在位置即可。

此处可利用一个小技巧：将数组后边都加上一个最大值INF，这样便不需要再额外判断某个数组中的值是否已经全部取完。

代码（未AC）：

#include 
#include 
#include 
#include 
using namespace std;

const int maxn = 1000010;
const int INF = 0x7fffffff; // 最大值 
int S1[maxn], S2[maxn];

int main()
{
	freopen("input.txt", "r", stdin);
	int n, m;
	scanf("%d", &n);
	for(int i=0; i<n; i++)
	{
		scanf("%d", &S1[i]);	
	}	
	S1[n] = INF; // 设置最大值，就不需要判断某一数值是否已经取完 
	
	scanf("%d", &m);
	for(int i=0; i<m; i++)
	{
		scanf("%d", &S2[i]);
	}
	S2[m] = INF; // 设置最大值，就不需要判断某一数值是否已经取完 
	
	int pos = (n+m-1)/2; // 中位数下标 
	int index = 0;
	int i = 0, j = 0;
	while(index < pos)
	{
		index++;
		if(S1[i] <= S2[j])
		{
			i++;
		}
		else 
		{
			j++;
		}
	}
	int ans = min(S1[i], S2[j]);
	printf("%d", ans);

	fclose(stdin);	
	return 0;
 }