电子线路(线性部分)——第二章 晶体三极管
晶体三极管
- 晶体三极管简介
- 结构特点
- 晶体三极管工作原理
- 内部载流子传输过程
- 电流传输方程
- 共基极(CB-Common Base)
- 共发射极(CE-Common Emitter)
- 共集电极
- 晶体三极管模型
- 埃伯尔斯-莫尔模型
- 晶体三极管共射等效电路
- 大信号模型
- 小信号模型
- 流控特性和压控特性
- 混合$\pi$型电路模型
- 三极管的伏安特性曲线
- 输入特性曲线族
- 基区宽度调制效应
- 输出特性曲线
- 晶体三极管频率参数
- 三极管的电路分析方法
- 图解法
晶体三极管简介
三极管又称双极性三极管(Bipolar Junction Transistor),简称BJT
结构特点
- 两种类型: { N P N 型 P N P 型 \begin{cases}NPN型\\PNP型\end{cases} {NPN型PNP型
- 三个电极: { 发 射 极 E ( E m i t t e r ) 基 极 B ( B a s e ) 集 电 极 C ( C o l l e c t o r ) \begin{cases}发射极E(Emitter)\\基极B(Base)\\集电极C(Collector)\end{cases} ⎩⎪⎨⎪⎧发射极E(Emitter)基极B(Base)集电极C(Collector)
- 两个PN结: { 发 射 结 ( E B 结 ) 集 电 结 ( C B ) \begin{cases}发射结(EB结)\\集电结(CB)\end{cases} {发射结(EB结)集电结(CB)
- 三个区: { 发 射 区 基 区 集 电 区 \begin{cases}发射区\\基区\\集电区\end{cases} ⎩⎪⎨⎪⎧发射区基区集电区
- 工艺特点: { 发 射 区 掺 杂 浓 度 高 基 区 薄 集 电 区 面 积 大 \begin{cases}发射区掺杂浓度高\\基区薄\\集电区面积大\end{cases} ⎩⎪⎨⎪⎧发射区掺杂浓度高基区薄集电区面积大
- 电路符号:

Ⅰ. 箭头的指向为发射结正偏时,实际电流方向
Ⅱ. 指向的中性区为N型半导体,比如PNP型,箭头指向的就是N区 - 工作条件:BJT是有源器件,要在一定的直流偏置下才能正常工作
- 三种工作模式: { 放 大 模 式 : 发 射 结 ( E B ) 正 偏 , 集 电 结 ( C B ) 反 偏 饱 和 模 式 : C B 和 E B 均 正 偏 截 止 模 式 : C B 和 E B 均 反 偏 \begin{cases}放大模式:发射结(EB)正偏,集电结(CB)反偏\\饱和模式:CB和EB均正偏\\截止模式:CB和EB均反偏\end{cases} ⎩⎪⎨⎪⎧放大模式:发射结(EB)正偏,集电结(CB)反偏饱和模式:CB和EB均正偏截止模式:CB和EB均反偏
(放大模式下是正向受控作用, I C , I E I_C,I_E IC,IE只受EB正偏电压控制,而不受CB结反偏电压影响)
晶体三极管工作原理
内部载流子传输过程
以NPN型三极管在放大工作模式下为例
-
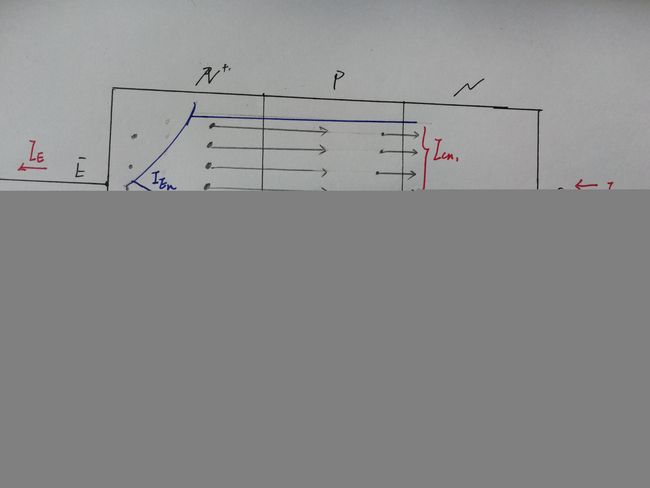
发射区掺杂浓度高,故EB结实际为 N + P N^+P N+P结,EB正偏,故电流以扩散电流为主,N区多子为电子,电子扩散运动朝P区并跨过P区到达CB结和N区,其扩散电流为 I E n I_{En} IEn,其下标E表示发射极的一部分电流,n表示电子作用的部分;相应的,P区的多子空穴也做扩散运动,其扩散电流为 I E p I_{Ep} IEp,然而掺杂浓度低,故电流也相应的比 I E n I_{En} IEn弱

-
因为P区的多子是空穴,所以电子在传输过程路过P区会有一部分电子脱离队伍和P区的空穴复合,(我们暂时先不标记这一部分电流,之后用基尔霍夫定理求解即可)。所以实际到达CB结的时候,只剩下了电流 I C n 1 I_{Cn1} ICn1
-
这时候再看CB结,因为CB结反偏,所以主要是少子作用的漂移电流,即N区的少子空穴向P区漂移,P区的少子电子向N区漂移,其电流分别是 I C n 2 , I C p I_{Cn2},I_{Cp} ICn2,ICp,其下标中C表示CB结电流,n1表示从 N + N^+ N+区扩散来的电流,n2表示CB结电子漂移电流,p表示CB结空穴漂移电流。把CB结总的反偏漂移电流用 I C B O I_{CBO} ICBO表示,其下标CB的的含义是CB结电流,O表示集电结E开路
-
电流关系:
Ⅰ. 发射区向基区注入电子,同时复合基区扩散过来的空穴,所以发射极的电流由两部分构成, 即 I E = I E n + I E p I_E=I_{En}+I_{Ep} IE=IEn+IEp
Ⅱ. 集电区要将热平衡空穴漂移到基区外,还要复合自基区漂移过来的所有电子(其中包括远渡重洋而来的 N + N^+ N+区的电子),所以集电极的电流 I C = I C n 1 + I C n 2 + I C p I_C=I_{Cn1}+I_{Cn2}+I_{Cp} IC=ICn1+ICn2+ICp
即 I E = I C B O + I C n 1 I_E=I_{CBO}+I_{Cn1} IE=ICBO+ICn1
Ⅲ. 由基尔霍夫定律,基极的电流 I B = I E − I C I_B=I_{E}-I_{C} IB=IE−IC
从图上看, I B = I E p + ( I E n − I C n 1 ) − I C B O I_B=I_{Ep}+(I_{En}-I_{Cn1})-I_{CBO} IB=IEp+(IEn−ICn1)−ICBO -
共基极电流传输系数:
简单来说,就是 I E I_E IE中有多少转换成了 I C n 1 I_{Cn1} ICn1,即 α ‾ = I C n 1 I E \overline{\alpha}=\frac{I_{Cn1}}{I_E} α=IEICn1简单来说,就是 I E I_E IE中有多少转换成了 I C n 1 I_{Cn1} ICn1,即 α ‾ = I C n 1 I E \overline{\alpha}=\frac{I_{Cn1}}{I_E} α=IEICn1
其中, I E I_E IE有 I E p I_{Ep} IEp和 I E n I_{En} IEn两部分,而 I E n I_{En} IEn占 I E I_E IE的部分成为发射区的发射效率,即 η E = I E n I E \eta_E=\frac{I_{En}}{I_E} ηE=IEIEn
而实际到达CB结的电流 I C n 1 I_{Cn1} ICn1在 I E n I_{En} IEn中的占比,称作基区传输效率,即 η B = I C n 1 I E n \eta_B=\frac{I_{Cn1}}{I_{En}} ηB=IEnICn1
所以 α ‾ \overline{\alpha} α又可以表示成 α ‾ = η E η B \overline{\alpha}=\eta_E\eta_B α=ηEηB -
寄生电流:在众多载流子流中间,唯有发射区中的多子自由电子通过发射结注入、基区扩散(复合)、集电结收集三个环节将发射结电流 I E n I_{En} IEn转换为集电结电流 I C n 1 I_{Cn1} ICn1,其大小仅仅受正偏发射结电压控制,而几乎不受反偏集电结电压控制,其他的载流子流只能分别产生两个结的电流而不会转换为另一个的电流,他们对于正向受控作用来说都是无用的,叫做三极管的寄生电流
-
减小寄生电流的方法:
- 发射结为不对成结,发射区的掺杂浓度远远高于基区
- 减小基区宽度,减少 I E n I_{En} IEn在传输过程中,跨国基区而被复合掉的几率
- 集电极面积大于发射结,这样可以保证CB结边界的少子充分的漂移到集电区,形成受控的集电结电流
电流传输方程
双端网络需四个端口,而三极管仅三个引脚,故需有两个端口共用一个引脚,总共三种组合,也就是三种连接方式,分别是共基极,共射(发射极),共集电极
共基极(CB-Common Base)
I C I_C IC和 I E I_E IE关系:
已知 α ‾ = I C n 1 I E = I C − I C B O I E \overline{\alpha}=\frac{I_{Cn1}}{I_E}=\frac{I_C-I_{CBO}}{I_E} α=IEICn1=IEIC−ICBO,所以 I C = α ‾ I E + I C B O I_C=\overline{\alpha}I_E+I_{CBO} IC=αIE+ICBO,而 I C B O I_{CBO} ICBO很小,可以忽略,于是, I C ≈ α ‾ I E I_C\approx \overline{\alpha}I_E IC≈αIE
共发射极(CE-Common Emitter)
连接方式如图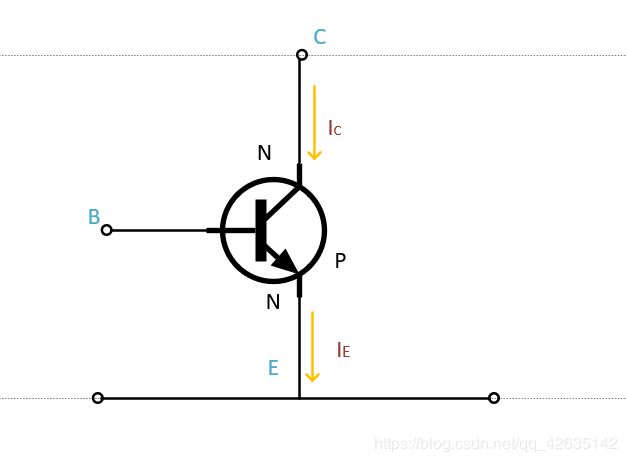
I C I_C IC和 I B I_B IB关系:
已知 I C = α ‾ I E + I C B O I_C=\overline{\alpha}I_E+I_{CBO} IC=αIE+ICBO,而 I E = I C + I B I_E=I_C+I_B IE=IC+IB
所以 I C = α ‾ 1 − α ‾ + 1 1 − α ‾ I C B O I_C=\frac{\overline{\alpha}}{1-\overline{\alpha}}+\frac{1}{1-\overline{\alpha}}I_{CBO} IC=1−αα+1−α1ICBO
这里定义共发射极电流放大系数 β ‾ = α ‾ 1 − α ‾ \overline{\beta}=\frac{\overline{\alpha}}{1-\overline{\alpha}} β=1−αα
并引入穿透电流 I C E O I_{CEO} ICEO,它是指基极开路( I B = 0 I_B=0 IB=0)的时候集电极的电流, I C E O = 1 1 − α ‾ I C B O I_{CEO}=\frac{1}{1-\overline{\alpha}}I_{CBO} ICEO=1−α1ICBO,即 I C E O = ( 1 + β ‾ ) I C B O I_{CEO}=(1+\overline{\beta})I_{CBO} ICEO=(1+β)ICBO
这时的 I C I_C IC和 I E I_E IE关系是 I C = β ‾ I B + I C E O I_C=\overline{\beta}I_B+I_{CEO} IC=βIB+ICEO
这里的 I C E O I_{CEO} ICEO同样很小,可忽略,所以 I C = β ‾ I B I_C=\overline{\beta}I_B IC=βIB
共集电极
连接方式如图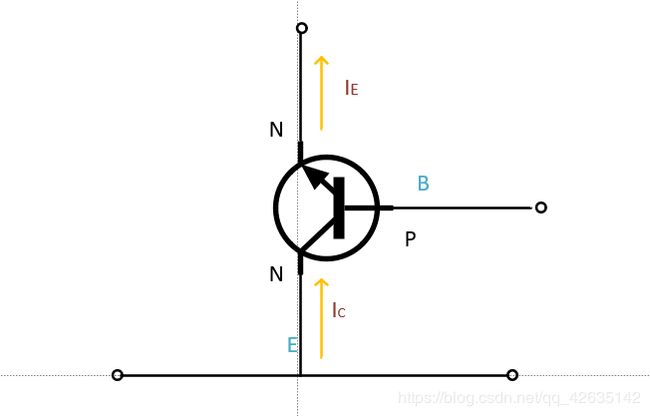
I B I_B IB和 I E I_E IE关系:
I C = α ‾ I E + I C B O I_C=\overline{\alpha}I_E+I_{CBO} IC=αIE+ICBO 、 I C = I E − I B I_C=I_E-I_B IC=IE−IB
⟹ I E = 1 1 − α ‾ ( I B + I C B O ) = ( 1 + β ‾ ) I B + I C B O \implies I_E=\frac{1}{1-\overline{\alpha}}(I_B+I_{CBO})=(1+\overline{\beta})I_B+I_{CBO} ⟹IE=1−α1(IB+ICBO)=(1+β)IB+ICBO
忽略 I C B O I_{CBO} ICBO,则 I E ≈ ( 1 + β ‾ ) I B I_E\approx(1+\overline{\beta})I_B IE≈(1+β)IB
(一般情况下,集电结不能做输入端,基极不能做输出端)
晶体三极管模型
埃伯尔斯-莫尔模型
有三极管的的结构可以大致看作是两个二极管背靠背组成
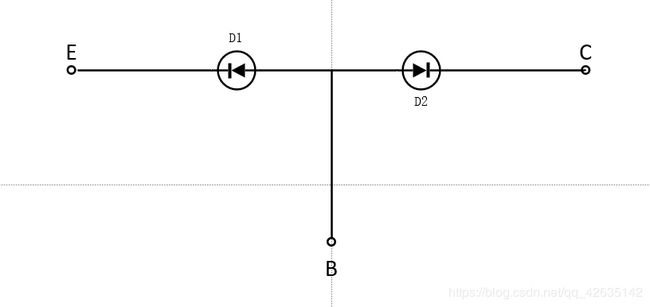
但是基区很窄,导致两个二极管相互影响,将这种影响用受控源表示,就是如下电路:
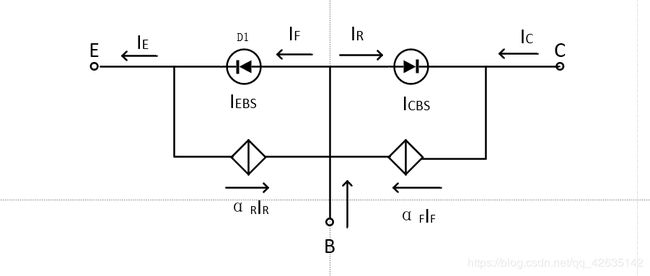
{ I F = I E B S ( e V B E V T − 1 ) I R = I E B S ( e V B C V T − 1 ) \begin{cases}I_F=I_{EBS}(e^{\frac{V_{BE}}{V_T}}-1)\\I_R=I_{EBS}(e^{\frac{V_{BC}}{V_T}}-1)\end{cases} ⎩⎨⎧IF=IEBS(eVTVBE−1)IR=IEBS(eVTVBC−1)
其中,如上述下标规则一样, I C B O I_{CBO} ICBO表示E断路,而 I C B S I_{CBS} ICBS,则表示E短路, I E B S I_{EBS} IEBS同理
推导过程略,直接给出结果: I E ≈ I E B S e V B E V T I_E\approx I_{EBS}e^{\frac{V_{BE}}{V_T}} IE≈IEBSeVTVBE I C ≈ α ‾ I E B S e V B E V T = I S e V B E V T I_C\approx\overline{\alpha}I_{EBS}e^{\frac{V_{BE}}{V_T}}=I_{S}e^{\frac{V_{BE}}{V_T}} IC≈αIEBSeVTVBE=ISeVTVBE
晶体三极管共射等效电路
大信号模型
- 放大模式:
由埃伯尔斯-莫尔等效模型,可将三极管等效成二极管和受控源,如图

此二极管的反向饱和电流为 I S β ‾ \frac{I_S}{\overline{\beta}} βIS
再将二极管用大信号模型表示,并忽略其导通电阻
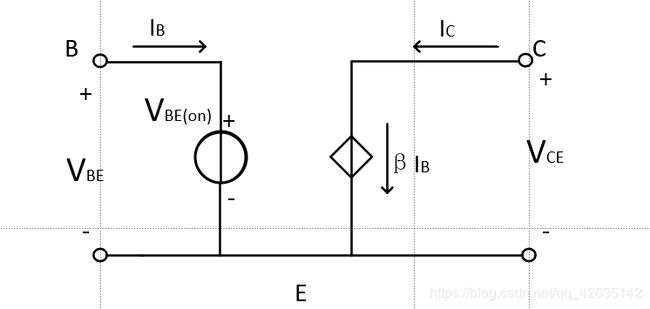
V B E ( o n ) V_{BE(on)} VBE(on)为发射结正向导通电压,这里取值 0.7 V 0.7V 0.7V
- 每升高1℃, Δ β ‾ / β ‾ \Delta \overline{\beta}/\overline{\beta} Δβ/β增大0.5%~1%,即 Δ β ‾ / ( β ‾ T ) = 0.005 ∼ 0.01 ℃ \Delta \overline{\beta}/(\overline{\beta}T)=0.005\thicksim 0.01℃ Δβ/(βT)=0.005∼0.01℃
- 每升高1℃, V B E ( o n ) V_{BE(on)} VBE(on)减小2~2.5mV,即 Δ V B E ( o n ) / Δ T = − ( 2 ∼ 2.5 m V / ℃ ) \Delta V_{BE(on)}/\Delta T=-(2\thicksim2.5mV/℃) ΔVBE(on)/ΔT=−(2∼2.5mV/℃)
- 每升高10℃, I C B O I_{CBO} ICBO增大一倍
- 饱和模式
等效原理同上
等效电路图如下

{ V B E ( s a t ) ≈ V B E ( o n ) = 0.7 V V B C ( s a t ) ≈ V B C ( o n ) = 0.4 V \begin{cases}V_{BE(sat)}\approx V_{BE(on)}=0.7V\\V_{BC(sat)}\approx V_{BC(on)}=0.4V\end{cases} {VBE(sat)≈VBE(on)=0.7VVBC(sat)≈VBC(on)=0.4V
结论:三极管失去正向受控作用。
小信号模型
表达式符号约定:
- 大写字母、小写下标表示直流量
- 小写字母、小写下标表示交流量
- 小写字母、大写下标表示总瞬时量
晶体三极管的小信号模型可以在其共发射极连接时的等效电路模型得到。
基极和发射极之间是一只等效而二极管,而根据二极管的小信号模型即可得到三极管的小信号模型。
在共发射极的模型中,利用小信号模型将二极管等效为一个电阻,记为 r b e r_{be} rbe,其是二极管的增量电阻称为三极管的“输入电阻”,由公式 r j = V T I D Q r_j=\frac{V_T}{I_{DQ}} rj=IDQVT,有 r b e = V T I B Q r_{be}=\frac{V_T}{I_{BQ}} rbe=IBQVT,在前面我们通过共集电极连接方式得出了 I B I_B IB和 I E I_E IE的关系: I E = ( 1 + β ) I B I_E=(1+\beta)I_B IE=(1+β)IB,便得到 r b e = ( 1 + β ) V T I E Q r_{be}=(1+\beta)\frac{V_T}{I_{EQ}} rbe=(1+β)IEQVT
流控特性和压控特性
i c = g m v b e = β i b i_c=g_mv_{be}=\beta i_b ic=gmvbe=βib
g m = I C Q V T g_m=\frac{I_{CQ}}{V_T} gm=VTICQ
混合 π \pi π型电路模型

电路低频工作时,可忽略结电容影响,因此低频混合 π \pi π 型电路模型简化为

其中, r b b ′ r_{bb'} rbb′是由基极引线电阻和基区体电阻组成,约为几十欧,而 r b ′ e r_{b'e} rb′e约为几千欧姆,因而 r b b ′ r_bb' rbb′可忽略,仅有在电流 I E Q I_{EQ} IEQ过大的时候才考虑
三极管的伏安特性曲线
输入特性曲线族
- 当 V C E V_{CE} VCE一定时,其类似于二极管的伏安特性曲线
- V C E V_{CE} VCE增加,时,正向特性曲线右移(基区宽度调制效应)
基区宽度调制效应

V C E = V C B + V B E V_{CE}=V_{CB}+V_{BE} VCE=VCB+VBE
当 V B E V_{BE} VBE一定时
V C E 增 加 ⟹ V C B 增 加 ⟹ 集 电 结 阻 挡 层 宽 度 增 加 ⟹ 基 区 宽 度 减 少 ⟹ 发 射 区 注 入 的 电 子 在 路 过 基 区 的 时 候 , 与 基 区 空 穴 复 合 几 率 变 小 ⟹ i B 减 小 V_{CE}增加\implies V_{CB}增加\implies 集电结阻挡层宽度增加\implies基区宽度减少\implies发射区注入的电子在路过基区的时候,与基区空穴复合几率变小\implies i_B减小 VCE增加⟹VCB增加⟹集电结阻挡层宽度增加⟹基区宽度减少⟹发射区注入的电子在路过基区的时候,与基区空穴复合几率变小⟹iB减小
输出特性曲线

输出特性曲线划分为四个区域:
{ 饱 和 区 放 大 区 截 止 区 击 穿 区 \begin{cases}饱和区\\放大区\\截止区\\击穿区\end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧饱和区放大区截止区击穿区
- 饱和区
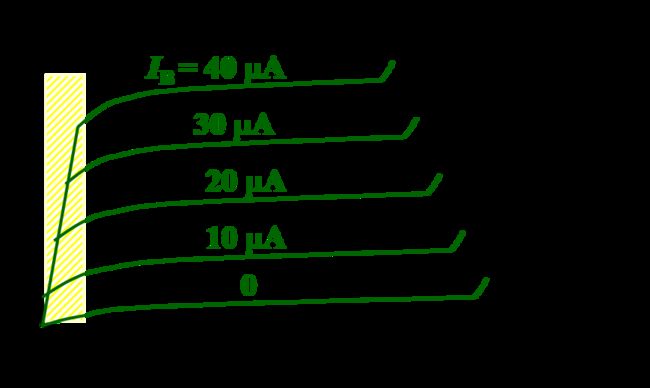
条件:发射结正偏,集电结正偏
特点: I C I_C IC不受 I B I_B IB控制,而受 V C E V_{CE} VCE影响; V C E V_{CE} VCE 略增, I C I_C IC 显著增加。 - 放大区

条件:发射结正偏,集电结反偏
特点: 具有正向受控作用、满足 I C = β I B + I C E O I_C = \beta I_B + I_{CEO} IC=βIB+ICEO、 V C E V_{CE} VCE增加会使曲线略上翘
上翘原因:基区宽度调制效应
上翘程度:取决于厄尔利电压 V A V_A VA, V A V_A VA越小,上翘越厉害
-
截止区( V B E ⩽ 0.5 V , V C E ⩾ 0.3 V V_{BE} \leqslant 0.5 V, V_{CE} \geqslant 0.3 V VBE⩽0.5V,VCE⩾0.3V)

条件:发射结正偏,集电结反偏
特点: I B ≈ 0 , I C ≈ 0 I_B\approx0,I_C\approx0 IB≈0,IC≈0 -
击穿区

特点: V C E V_{CE} VCE 增大到一定值时,集电结反向击穿, I C I_C IC 急剧增大。集电结反向击穿电压,随 I B I_B IB的增大而减小。
{ 反 向 击 穿 : 主 要 是 雪 崩 击 穿 穿 通 击 穿 : 三 极 管 特 有 击 穿 , 指 基 区 很 小 的 三 极 管 中 , 因 集 电 结 阻 挡 层 宽 度 过 大 , 导 致 基 区 消 失 \begin{cases}反向击穿:主要是雪崩击穿\\穿通击穿:三极管特有击穿,指基区很小的三极管中,因集电结阻挡层宽度过大,导致基区消失\end{cases} {反向击穿:主要是雪崩击穿穿通击穿:三极管特有击穿,指基区很小的三极管中,因集电结阻挡层宽度过大,导致基区消失
-
三极管安全工作区

要求: { I C ⩽ I C M V C E ⩽ V ( B R ) C E O P C ⩽ P C M \begin{cases}I_C\leqslant I_{CM}\\V_{CE}\leqslant V_{(BR)CEO}\\P_C\leqslant P_{CM}\end{cases} ⎩⎪⎨⎪⎧IC⩽ICMVCE⩽V(BR)CEOPC⩽PCM
最大允许集电极电流 I C M I_{CM} ICM
反向击穿电压 V ( B R ) C E O V_{(BR)CEO} V(BR)CEO
最大允许集电极耗散功率 P C M P_{CM} PCM
晶体三极管频率参数
β ( j ω ) = β 1 + j ω ω β \beta(j\omega)=\frac{\beta}{1+\frac{j\omega}{\omega_\beta}} β(jω)=1+ωβjωβ
取模:
∣ β ( ω ) ∣ = β 1 + ( ω ω β ) 2 |\beta(\omega)|=\frac{\beta}{\sqrt{1+(\frac{\omega}{\omega_\beta}})^2} ∣β(ω)∣=1+(ωβω)2β
{ 工 作 频 率 远 低 于 β ω 时 , β ( ω ) = β ω = ω β 时 , ω ( β ) = 0.707 β ω ≫ ω β 时 , β ( ω ) = β ω β ω \begin{cases}工作频率远低于\beta_\omega时,\beta(\omega)=\beta\\\omega=\omega_\beta时,\omega(\beta)=0.707\beta\\\omega\gg\omega_\beta时,\beta(\omega)=\frac{\beta\omega_\beta}{\omega}\end{cases} ⎩⎪⎨⎪⎧工作频率远低于βω时,β(ω)=βω=ωβ时,ω(β)=0.707βω≫ωβ时,β(ω)=ωβωβ
特征角频率 ω T \omega_T ωT: β = 1 \beta=1 β=1对应的角频率叫特征角频率,其物理含义是,该频率下,三极管失去放大作用
ω T = β ω β \omega_T=\beta\omega_\beta ωT=βωβ
三极管的电路分析方法
图解法
即利用三极管的输入、输出特性曲线与管外电路所确定的负载线,通过作图的方法进行求解

利用输入特性曲线( I b I_b Ib与 v B E v_{BE} vBE关系)和管外负载线交点
+输出特性曲线( I c I_c Ic与 v C E v_{CE} vCE关系)和管外负载线交点







