一键修复“一看就会,一学就废”bug——动态规划
阿伟在搞蓝桥杯的时候,属实是被动态规划按在地上摩擦、吊在树上打,看的懂答案、但是做的时候老是白给,于是我赶紧去找大佬的文章去读一下(可以看我下面的参考资料),下面是我自己的一些见解,希望在自己成长的同时,可以帮助到有需要的人。该文章用leetcode《53. 最大子序和》作为开始,leetcode《5. 最长回文子串》进阶和强化,leetcode《887. 鸡蛋掉落》做魔鬼训练,实际代码以及代码模板均用伪代码,后面有题目类型总结(看来源),建议点个小星星作为收藏,方便练习
白话解动态规划
- 1. 动态规划究竟是要干什么
- 2. 动态规划的思考步骤
- 3. 最大子序列和(入门难度,了解思维方式)
- 3.1 题目描述
- 3.2 那么好,这里用我的三个步骤进行分析
- 3.3 那么好,经过三个思维步骤确定了状态转移方程,就可以直接打伪代码了
- 3.4 做完了,进行入门题目的总结
- 4. 最长回文子串(medium难度,熟练一下)
- 4.1 题目描述
- 4.2 按照三个步骤进行分析
- 4.3 好,可以直接写出伪代码
- 4.4 该题总结
- 5. 知道了刷题的套路,再回头深入理解动态规划的本质,为什么动态规划会这么6
- 6. 高楼砸鸡蛋问题(hard难度,带着状态变化思考问题)
- 6.1 题目讲述
- 6.2 在正式解题前,吹一波水,稳住
- 6.3 等一下,我这题直接用二分搜索不就完事了嘛
- 6.4 三个思考步骤
- 6.5 构建伪代码
- 6.6 其实呢,这题还是有办法二分的
- 6.7 来一波反向操作,看一下你懂了没
- 7. 动态规划的题目练习(leetcode)——有生之年系列,来源于潮汐的知乎专栏
- 7.1 线性DP
- 7.2 区间DP
- 7.3 背包DP
- 7.4 树形DP
- 7.5 状态压缩DP
- 7.6 数位DP
- 7.7 计数型DP
- 7.8 递推型DP
- 7.9 概率型DP
- 7.10 博弈型DP
- 7.11 记忆化搜索
- 8. 优化问题
- 9. 总结:
- 9.1 动态规划的适用场景
- 9.2 动态规划的思考步骤
- 10. 参考资料:
1. 动态规划究竟是要干什么
动态规划就是暴力解决问题(穷举法),但是动态规划是练过军体拳的、一拳一个嘤嘤怪(穷举的优化),一般的穷举法是乱拳打老师傅、一大通王八拳完事(直接暴力)。动态规划的核心思想就是用一个备忘录将子问题的最优解全部叠加起来,将一个个小的问题进行叠加变成大问题,叠到最后就是整个问题的最优解。说的通俗一点就是:大事化小,小事化了,一般而言,他解决的求最值问题具有以下三个特征:
- 暴力穷举的时候,存在重叠子问题:通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,具有天然剪枝的功能,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。比较人话一点:上一个解决的子问题,可以用作下一个子问题的参考答案(又不是西方国家抗疫,抄都不会抄)。有的直接就抄,所以用一个备忘录来记录下解决过的东西,再遇到直接抄就完事了,从而减低了时间复杂度。
- 子问题存在最优子结构:每一个小的部分都可以找到各自在这个阶段的最优解,最后每一个小的子问题的最优解叠加起来起到质变得到最终解。
- 存在状态转移方程:上一个子问题可以通过某种方式(加上一些东西)变成下一个子问题的答案。
如果将已经学过的东西进行纵向对比的话,我觉得所谓的动态规划特别像高中数学的送(na)分(ming)题——等差数列里面通过A1和d确定An的值

其实动态规划的代码并不长,正所谓浓缩的就是精华,但是他的状态转移方程构建和重叠子问题的消除就很难,没什么关系,下面会有三个思考步骤,帮助构建状态转移方程。在这里,我不会去弄教科书里面什么自顶向下的办法之类的,那种花里胡哨的,我是怎么实用怎么来,在熟悉了动态规划的思考方式之后,我会再回到概念上加深理解。
2. 动态规划的思考步骤
其实leetcode题目medium难度已经是面试正常题目的难度了,hard难度的话都是面试中比较难的题目,所以medium难度多做一道作为训练,hard只有一道,想多做的话建议自己看后面的有生之年系列去练习
其实动态规划的三个步骤和“等差数列里面通过A1和d确定An的值”的求解思路,区别不大,思想都是找到“d”和“a0”,确定ak。(下标不好打,看间隔)
- 定义子问题的最优解(ak-2与ak-1)的含义(我是谁),动态规划毕竟不是等差数列,ak-2与ak-1并不是一个具体的数字,在解题中需要确定ak-2与ak-1是什么形式,是一个最长距离还是一个true or false 的flag,那么才好放到备忘录中消除重叠子问题,也方便确定最后解的形式。
- 找到“ak+1 = ak + d”这个方程式,确定子问题之间的递推关系(我要到哪里去),放在等差数列中就是找d,这就需要一点数学知识,稳住,这是最难的一部分了,但是稳住别慌,问题不大在涉及到递归的状态转移方程:有一个用于递归的思维框架(这个我是看Github项目《labuladong/fucking-algorithm》知道的,在解决确实好用):
明确「状态」 -> 定义 dp 数组/函数的含义 -> 明确「选择」-> 明确 base case。 - 找到初始值a0(我从哪里来),由零开始一层层往上走。
有了初始值,并且有了数组元素之间的关系式,那么我们就可以得到 dp[n] 的值了,而 dp[n] 的含义是由你来定义的,你想求什么,就定义它是什么,这样,这道题也就解出来了。
那么好,我们用例题进行讲解,因为确实干写干读实在太过于枯燥了。
3. 最大子序列和(入门难度,了解思维方式)
来源:leetcode《53. 最大子序和》
3.1 题目描述
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。

很巧的是这题有视频讲解,我可能讲的不太好,可以看这个视频:
官方题解,那里就有,一点开就可以了,b站链接:53. 最大子序和 Maximum Subarray 【LeetCode 力扣官方题解】
3.2 那么好,这里用我的三个步骤进行分析
来,拿出我们的小纸纸,对着例题来进行分析。
1.定义子问题的最优解(ak-2与ak-1)的含义。(我是谁)
题目问的是:给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。那么在这里直接找第k个数所对应的最大子序列之和不就完事了吗,用例子算一下先,嗯,怎么:
4 -1 2 1 -5找到的最大子序列是4 -1 2 1 ,4 -1 2 1 -5 4 找的还是 4 -1 2 1
这样子问题就重复了,想一想先,为什么重复,重复就是因为我停下来之后还使劲往前蹦跶,做别人的事情,那不是累死自己吗,那如果我直接在4 -1 2 1 -5 4的4那里刹住车,我也不往前面跳,我就踏踏实实的管住我门前的三亩地(也就是只管2 1 -5 4又或者是-1 2 1 -5 4,而不是4 -1 2 1)那不就ok了,如果每个数都管好自己的三亩地,并且把这个最大值记录下来,就不需要再往前跳(重复计算),我就可以少走一点路,趴在床上刷手机不妙吗,最后我再把这些记录来个全部比较大小不就完事了吗
所以:找到当前位置第k个数结尾所对应的最大连续子序列之和,最后直接返回a0,a1……an之间最大值ak。
比较动态的过程可以看上面视频。
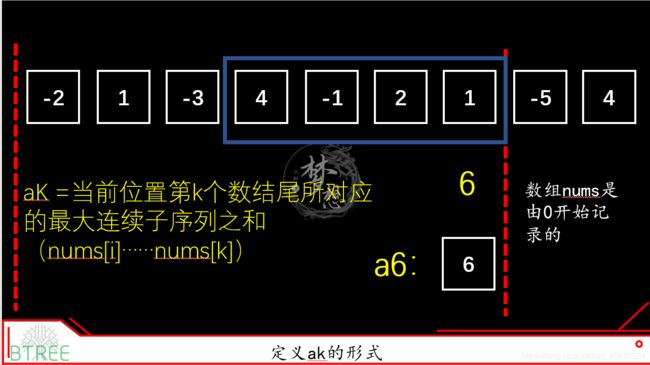
2.找到“ak+1 = ak+ d”这个方程式,确定子问题之间的递推关系。(我要到哪里去)
来看一下ak与ak-1
ak = 当前位置第k个数结尾所对应的最大连续子序列之和(nums[i]……nums[k])
ak+1 = 当前位置第k个数结尾所对应的最大连续子序列之和(nums[i]……nums[k],nums[k+1])
那么可以看到,两者之间的差别就在多了个nums[k+1],而ak的设定是当前位置第k个数结尾所对应的最大连续子序列之和,那么就比较num[k+1]单独成为一段与ak+nums[k+1]连接成段之间的大小,选取两者之间最大的那一个作为a[k]
所以得出状态转移方程:a[k+1] = max(ak + nums[k+1],nums[k+1])。
3.找到初始值a0,由零开始一层层往上走。(我从哪里来)
这个就简单了,初始值a0 = nums[0]
3.3 那么好,经过三个思维步骤确定了状态转移方程,就可以直接打伪代码了
1. MAX-SUB-ARRAY(nums)
2. maxAnswer = nums[0] //k = 0的情况
3.
4. //当前位置第k个数结尾所对应的最大连续子序列之和(nums[0]……nums[k])
5. pre = 0
6.
7. for i = 0 to the length of the nums,i++
8. pre = max(pre+nums[i],nums[i])
9. maxAnswer = max(maxAnswer,pre)
10. //直接比较可以减低空间复杂度,从O(N)(额外数组保存当前的最大值)降低到O(1)
11. end for
12. return maxAnswer
3.4 做完了,进行入门题目的总结
步骤一:在当前可能子情况不太明确的时候,可以把问题所问的整体改成局部(给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。变成第k个数所对应的最大子序列之和),然后用例子进行分析,做个人肉计算机,看一下算到哪里的时候会重复,发现重复的点就可以开始思考改正的方式,最后确定ak的形式。
步骤二:确定了形式,通过ak+1和ak之间形式的比较,以此确定两者之间的关系,当然对着例子是最方便的
步骤三:这个就看最小的时候是什么情况,没什么诀窍。
4. 最长回文子串(medium难度,熟练一下)
leetcode《5. 最长回文子串》
再做一道题,去熟悉一下,这里我不会讲的这么细,让读者自行思考一下(其实,就是懒得写)
4.1 题目描述
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

4.2 按照三个步骤进行分析
1.定义子问题的最优解(ak-2与ak-1)的含义。(我是谁)
这个就比较简单是能够一眼看出来的,ak = s[i]……s[j]是否为回文字符串的标志,是回文字符串则为true否则为false,如果最后a[i,j]到最后还是true,而且长度比较长,那就返回他的长度就完事了。那么考虑到他存储的是一个子字符串s[i]……s[j],所以这里应该用二维数组来保留 i(最左边的范围)与 j(最右边的范围):(在设置备忘录的元素含义的时候,也要考虑备忘录存储格式问题)
ak[ i ][ j ] = s[i]……s[j]是否为回文字符串的标志,是回文字符串则为true否则为false,如果最后a[i,j]到最后还是true,而且长度比较长,那就返回他就完事了。

2.找到“ak+1 = ak+ d”这个方程式,确定子问题之间的递推关系。(我要到哪里去)
这个问题嘛,画个图就了
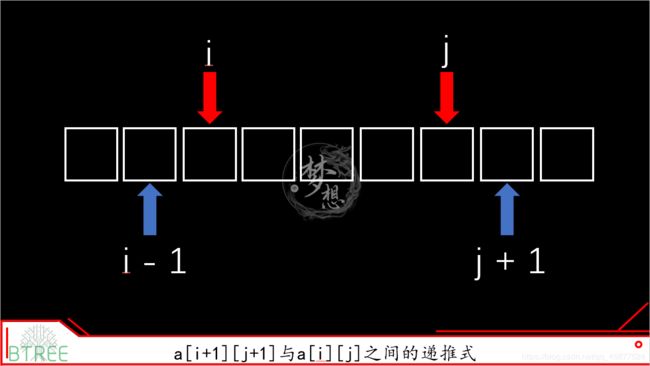
那很明显了,如果新加入的s[ i ][ j ]与a[ i ][ j ]都是true那就直接完事了,有一个是false那就歇逼。
换到方程式里面就是:

3.找到初始值a0,res = “ “为空字符串(我从哪里来)
4.3 好,可以直接写出伪代码
1. LONGEST-PALINDOMIC-SUBSTRING(s)
2. res = " "
3. n = the lenngth of the s
4. dp = [][]
5. for i = n - 1 to i = 0
6. for j = i to n
7. dp[i][j] = ( s[j] == s[j] ) && ( j - i < 2 ||dp[i + 1][j - 1]) //判断是否为回文字符串方程
8. if dp[i][j] == true && j - i + 1 > the length of the res
9. res = the substring from s[i] to s[j + 1] //比现在长就加进去
10. end if
11. end for
12. end for
13. return res
4.4 该题总结
要注意备忘录的存储格式问题,不仅仅只有一维数组。
5. 知道了刷题的套路,再回头深入理解动态规划的本质,为什么动态规划会这么6
那么好,到这里我相信都已经对动态规划怎么样思考,已经有点概念,对于怎么写应该有点数,但有了刷题的外功,没点内功还是花拳绣腿几下歇逼,因此回到动态规划的概念上,并且解决一个连在一起的问题:
什么是动态规划(Dynamic Programming)?动态规划的意义是什么?
在这里我建议直接看知乎用户王勐对问题的回答《什么是动态规划(Dynamic Programming)?动态规划的意义是什么?》,这个是比较直觉性的,比较严谨的带数学的看知乎用户覃含章对问题的回答《什么是动态规划(Dynamic Programming)?动态规划的意义是什么?》
该文章对于为什么需要动态规划,可以说是非常清楚,去看一下,再看下面的题目,你才能有更加深刻的理解。
精华摘要:
所谓的空间复杂度就是为了支持你的计算所必需存储的状态最多有多少,所谓时间复杂度就是从初始状态到达最终状态中间需要多少步!
对于状态转移方程,而言每求一个新数字只需要之前的两个状态。所以同一个时刻,最多只需要保存两个状态,空间复杂度就是常数;每计算一个新状态所需要的时间也是常数且状态是线性递增的,所以时间复杂度也是线性的。
动态规划对于贪心、递推、搜索之间有什么区别?
一个问题是该用递推、贪心、搜索还是动态规划,完全是由这个问题本身阶段间状态的转移方式决定的!每个阶段只有一个状态->递推;每个阶段的最优状态都是由上一个阶段的最优状态得到的->贪心;每个阶段的最优状态是由之前所有阶段的状态的组合得到的->搜索;每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的->动态规划。
6. 高楼砸鸡蛋问题(hard难度,带着状态变化思考问题)
leetcode《887. 鸡蛋掉落》
那么好,看完了前面的easy难度,是时候将难度进阶到面试中、考研上机的较难难度了,不要慌张,我会尽可能说明白,有视频不慌,·一道题不够,下面有生之年系列走起。
6.1 题目讲述
将获得 K 个鸡蛋,并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的,如果一个蛋碎了,你就不能再把它掉下去。(也就是一个鸡蛋没有碎,你可以继续往下丢,话说这算不算高空掷物,要去b站@一下罗老师先,看一下能不能把这个法外狂徒张三按在地上锤一顿)
你知道存在楼层 F,满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎,从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动,你可以取一个鸡蛋(如果你有完整的鸡蛋)并把它从任一楼层 X 扔下(满足 1 <= X <= N)。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何,你确定 F 的值的最小移动次数是多少?


吐槽一下,官方题解那一大堆文字(一堆公式,数学论文的既视感)属实没看懂,看视频倒是看懂了。
b站上有个很高播放量的视频也讲解了这个题目可以去看一下:
b站视频李永乐老师官方《复工复产找工作?先来看看这道面试题:双蛋问题》
leetcode官方也有视频(我没看懂,但是我的最后一个优化的代码是参考了官方的代码):
6.2 在正式解题前,吹一波水,稳住
这道题也是个老面试题了,不过说个实在话,动态规划能玩出个什么花样,无非就是一个dp方程,加上一个备忘录的利用,就是一个用空间换时间的优化版本穷举。奥里给
该题题解参考了:leetcode的 887. 鸡蛋掉落题目 labuladong的题解《题目理解 + 基本解法 + 进阶解法》
6.3 等一下,我这题直接用二分搜索不就完事了嘛
不行啊,鸡蛋够肯定可以往死里砸,但是现在问题是鸡蛋不够啊,你看如果你只有一个鸡蛋八层楼,你直接从4楼丢了下去,运气不好直接碎了就歇逼了,这种情况肯定也只能从一楼一路走上去。懂我意思吧,鸡蛋不够要省着点花。
6.4 三个思考步骤
1.定义子问题的最优解(ak-2与ak-1)的含义(我是谁),在这里由于有两个状态一个是楼层N一个是鸡蛋的数量K,因此用一个二维数组a[ i ][ j ]存储当前i个鸡蛋和j个楼层高度的时候,最少丢鸡蛋的次数。

2.找到“ak+1 = ak + d”这个方程式,确定子问题之间的递推关系(我要到哪里去),这时候考虑到两种情况,
- 鸡蛋碎了,那么 鸡蛋数目K应该减一,同时也要从当前楼层j往下移动。
- 如果 鸡蛋没有碎,那就往上移动,鸡蛋数目保持不变
因为我们要求的是 最坏情况下丢鸡蛋的次数,也就是意味着,鸡蛋在第 j 层没有炸,取得是往上走和往下走之间值最大的那一个。所以应该选择:
max(dp(K - 1,j - 1),dp(K,N - j))来获取在当前第j层最坏情况下扔鸡蛋的数目, 等一下,还有个最少次数,那就设立一个res去保留之前楼层所丢下鸡蛋的最小次数并且与当前的进行比较,看一下谁比较少,也就是说:
res = min(res,max(dp(K,N - i),dp(K - 1,i - 1))+ 1)
由于往上和往下走的探索方式一样,探索到最后都是把鸡蛋砸完或者是鸡蛋往下走楼层到底了,所以在这里采用递归的方式。
7.dp(K,N)
6. //基准情况
7. if K == 1
8. return N //只剩下一个鸡蛋,玩个锤子,最坏情况肯定是该楼层刚刚好
9. if N == 0
10. return 0 //楼层丢完了,就可以结束子情况
11.
12. if (K,N) in memeo
13. return memo[(K,N)] //如果子情况之前已经记录过,那就直接跳过
14.
15. for i to the N + 1 //穷举所有可能出现的情况,注意要从地面0开始往上算
16. res = min(res,max(dp(K,N - i),dp(K - 1,i - 1))+ 1)
17. end for
18.
19. memo[(K,N)] = res //放入备忘录中
20. return res //返回在当前N与K的数量时候,所需要的最小移动次数
3.初始值,这题没有初始值,每一个状态都要自己进行探索,如果硬说的话,基准情况可以作为初始值
6.5 构建伪代码
//方便理解版本
1.SUPER-EGG-DROP(K,N)
3. return dp(K,N)
4.
4.memo = {} //把备忘录,做成全局变量,用来记录每个不同时期子情况的值
5.
6.//动态规划方程
7.dp(K,N)
6. //基准情况
7. if K == 1
8. return N //只剩下一个鸡蛋,玩个锤子,从一楼往上扔吧
9. if N == 0
10. return 0 //楼层丢完了,就可以结束子情况
11.
12. if (K,N) in memeo
13. return memo[(K,N)] //如果子情况之前已经记录过,那就直接跳过
14.
15. for i to the N + 1 //穷举所有可能出现的情况,注意要从地面0开始往上算
16. res = min(res,max(dp(K,N - i),dp(K - 1,i - 1))+ 1)
17. end for
18.
19. memo[(K,N)] = res //放入备忘录中
20. return res //返回在当前N与K的数量时候,所需要的最小移动次数
6.6 其实呢,这题还是有办法二分的
//加上二分的版本
1.SUPER-EGG-DROP(K,N)
2. return dp(K,N)
3.
4.memo = {} //把备忘录,做成全局变量,用来记录每个不同时期子情况的值
5.
6.//动态规划方程
7.dp(K,N)
8. //基准情况
9. if K == 1
10. return N //只剩下一个鸡蛋,玩个锤子,从一楼往上扔吧
11. if N == 0
12. return 0 //楼层丢完了,就可以结束子情况
13.
14. //注意开始和前面的开始不一样
15. low = 1,high = N //开始往中间夹
16. while low <= high
17. mid = (low + high)/2
18. the number of broken = dp(K - 1,mid - 1) //碎了
19. the number of not broken = dp(K,N - mid) //没碎
20.
21. // res = min(res,max(the number of broken,the number of not broken) + 1)
22. if the number of broken > the number of no broken then
23. high = mid - 1
24. res = min(res,the number of broken + 1)
25. else
26. low = mid + 1
27. res = min(res,the number of not broken + 1)
28. end if
29. end while
30. memo[(K,N)] = res //放入备忘录中
31. return res //返回在当前N与K的数量时候,所需要的最小移动次数
6.7 来一波反向操作,看一下你懂了没
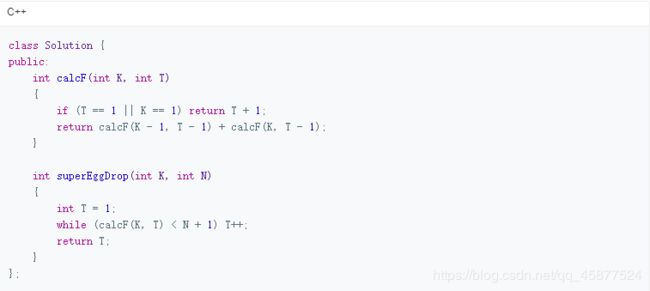
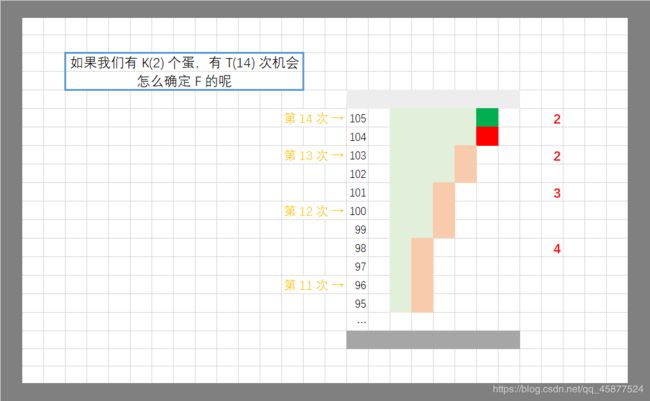
这一部分来源:Ikaruga的题解《【鸡蛋掉落】5行代码,从求扔几次变为求测多少层楼 =附面试经历=》
注意来源,这里不用做商用,只是作为学习笔记分享,本文章没有任何收益,如果侵权该部分立即删除

7. 动态规划的题目练习(leetcode)——有生之年系列,来源于潮汐的知乎专栏
注意这一部分,博主没有亲自收集,博主也是看别人的文章过来的,如果可以去帮别人点个赞吧。如果造成侵权(该部分并非商用,只是用作学习笔记),立马删除,不多bb。
潮汐的知乎专栏《[力扣] DP问题分类汇总》
我也准备按照它的题目分类去做一遍,大佬nb,大佬的分类是真好。
7.1 线性DP
最经典单串:《300. 最长上升子序列》
最经典的双串:《1143. 最长公共子序列》
经典问题:
leetcode题目《120. 三角形最小路径和》、《53. 最大子序和》、《152. 乘积最大子数组》、《887. 鸡蛋掉落 (DP+二分)》、《354. 俄罗斯套娃信封问题 (隐晦的LIS)》
打家劫舍系列: (打家劫舍3 是树形DP)
《198. 打家劫舍》、《213. 打家劫舍 II》
股票系列:
《121. 买卖股票的最佳时机》、《122. 买卖股票的最佳时机 II》、《123. 买卖股票的最佳时机 III》、《188. 买卖股票的最佳时机 IV》、《309. 最佳买卖股票时机含冷冻期》、《714. 买卖股票的最佳时机含手续费》
字符串匹配系列
《72. 编辑距离》、《44. 通配符匹配》、《10. 正则表达式匹配》
7.2 区间DP
《516. 最长回文子序列》、《730. 统计不同回文子字符串》、《1039. 多边形三角剖分的最低得分》、《664. 奇怪的打印机》、《312. 戳气球》
7.3 背包DP
《416. 分割等和子集 (01背包-要求恰好取到背包容量)》、《494. 目标和 (01背包-求方案数)》、《322. 零钱兑换 (完全背包)》、《518. 零钱兑换 II (完全背包-求方案数)》、《474. 一和零 (二维费用背包)》
7.4 树形DP
《124. 二叉树中的最大路径和》、《1245. 树的直径 (邻接表上的树形DP)》、《543. 二叉树的直径》、《333. 最大 BST 子树》、《337. 打家劫舍 III》
7.5 状态压缩DP
《464. 我能赢吗》、《526. 优美的排列》、《935. 骑士拨号器》、《1349. 参加考试的最大学生数》
7.6 数位DP
《233. 数字 1 的个数》、《902. 最大为 N 的数字组合》、《1015. 可被 K 整除的最小整数》
7.7 计数型DP
计数型DP都可以以组合数学的方法写出组合数,然后dp求组合数
《62. 不同路径》、《63. 不同路径 II》、《96. 不同的二叉搜索树 (卡特兰数)》、《1259. 不相交的握手 (卢卡斯定理求大组合数模质数)》
7.8 递推型DP
所有线性递推关系都可以用矩阵快速幂做,可以O(logN),最典型是斐波那契数列
《70. 爬楼梯》、《509. 斐波那契数》、《935. 骑士拨号器》、《957. N 天后的牢房》、《1137. 第 N 个泰波那契数》
7.9 概率型DP
求概率,求数学期望
《808. 分汤》、《837. 新21点》
7.10 博弈型DP
策梅洛定理,SG定理,minimax
《293. 翻转游戏》、《294. 翻转游戏 II》、《292. Nim 游戏》、《877. 石子游戏》、《1140. 石子游戏 II》、《348. 判定井字棋胜负》、《794. 有效的井字游戏》、《1275. 找出井字棋的获胜者》
7.11 记忆化搜索
本质是 dfs + 记忆化,用在状态的转移方向不确定的情况
《329. 矩阵中的最长递增路径、《576. 出界的路径数》
8. 优化问题
其实我认为优化改进集中在初始化定义哪里,确定的好就ok确定不好就歇逼,和我第一题一样,其实真的没有什么诀窍,做多一点题,吃多一点亏,再做题才能看到,因为你脑子里面根本没有优化的方向的话,再怎么分析也是歇逼
9. 总结:
本文还是实用解题为主,因此总结了动态规划的适用场景和思考步骤
9.1 动态规划的适用场景
- 子问题的答案依赖于问题的规模,也就是子问题的所有答案构成了一个数列
- 大规模问题的答案可以由小规模问题的答案递推得到
9.2 动态规划的思考步骤
动态规划的三个步骤可以概括成三个步骤:我是谁,我要去哪里,我从哪里来。
- 定义子问题的最优解(ak-2与ak-1)的含义(我是谁)
- 找到“ak+1 = ak + d”这个方程式,确定子问题之间的递推关系(我要去哪里)
- 找到初始值a0(我从哪里来),由零开始一层层往上走。
有了初始值,并且有了数组元素之间的关系式,那么我们就可以得到 dp[n] 的值了,而 dp[n] 的含义是由你来定义的,你想求什么,就定义它是什么,这样,这道题也就解出来了。
10. 参考资料:
- leetcode《887. 鸡蛋掉落》leetcode的 887. 鸡蛋掉落题目 labuladong的题解《题目理解 + 基本解法 + 进阶解法》、 Ikaruga的题解《【鸡蛋掉落】5行代码,从求扔几次变为求测多少层楼 =附面试经历=》
- leetcode《53. 最大子序和》,以及灵魂画手的题解《画解算法:53. 最大子序和》
- leetcode《5. 最长回文子串》,以及windliang的题解《详细通俗的思路分析,多解法》
- CSDN博主mmc2015的《非常好的动态规划总结,DP总结》、CSDN博主BS有前途的《经典中的经典算法:动态规划(详细解释,从入门到实践,逐步讲解)》、CSDN博主HankingHu的《算法-动态规划 Dynamic Programming–从菜鸟到老鸟》
- 帅地的知乎专栏《告别动态规划,连刷 40 道题,我总结了这些套路,看不懂你打我(万字长文)》、 潮汐的知乎专栏《[力扣] DP问题分类汇总》
- 博客园博主英雄哪里出来的《夜深人静写算法(二) - 动态规划》
- Github项目《labuladong/fucking-algorithm》,b站leetcode官方的《887. 鸡蛋掉落 Super Egg Drop 【LeetCode 力扣官方题解】》
- b站视频李永乐老师官方《复工复产找工作?先来看看这道面试题:双蛋问题》
- 我自己的博客《回溯算法以及剪枝技巧(内附通用构建模板,文末有C++、JAVA、Python的实现)》
- 知乎用户王勐对问题的回答《什么是动态规划(Dynamic Programming)?动态规划的意义是什么?》,知乎用户zhen tan对问题的回答《如何理解动态规划?》,知乎用户覃含章对问题的回答《什么是动态规划(Dynamic Programming)?动态规划的意义是什么?》,知乎用户阮行止在该问题的回答
- 算法导论P202-P236




