leetcode数组中的问题(四)
目前,遇到的滑动窗口,大体有两种思路右指针每次都右移,左指针依条件看是否要更新,但是右指针必定更新;直接依条件移动左右指针,每次必定会移动一个指针。
目录
541. 反转字符串 II
557. 反转字符串中的单词 III
11. 盛最多水的容器
209. 长度最小的子数组
325. 和等于 k 的最长子数组长度
718. 最长重复子数组
303. 区域和检索 - 数组不可变
304. 二维区域和检索 - 矩阵不可变
3. 无重复字符的最长子串
159. 至多包含两个不同字符的最长子串
541. 反转字符串 II
https://leetcode-cn.com/problems/reverse-string-ii/submissions/
给定一个字符串和一个整数 k,你需要对从字符串开头算起的每个 2k 个字符的前k个字符进行反转。如果剩余少于 k 个字符,则将剩余的所有全部反转。如果有小于 2k 但大于或等于 k 个字符,则反转前 k 个字符,并将剩余的字符保持原样。
示例:输入: s = "abcdefg", k = 2,输出: "bacdfeg"
要求:该字符串只包含小写的英文字母。给定字符串的长度和 k 在[1, 10000]范围内。
思路
一:与344反转字符串一个思路,只不过是每隔2k反转前k个元素,O(n)时间复杂度。
class Solution(object):
def reverseStr(self, s, k):
"""
:type s: str
:type k: int
:rtype: str
"""
s_l = list(s)
for i in range(0, len(s), 2 * k):
# 寻找每2k中的前k,若[l,r]中的元素不足k,则取到S的末尾即可
l, r = i, min(i + k - 1, len(s) - 1)
while l < r:
s_l[l], s_l[r] = s_l[r], s_l[l]
l += 1
r -= 1
return "".join(s_l)557. 反转字符串中的单词 III
https://leetcode-cn.com/problems/reverse-words-in-a-string-iii/
给定一个字符串,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
示例 1:输入: "Let's take LeetCode contest",输出: "s'teL ekat edoCteeL tsetnoc"
注意:在字符串中,每个单词由单个空格分隔,并且字符串中不会有任何额外的空格。
思路
一:先将字符串按空格分割,得到一个单词列表,列表中的元素是字符串,由于字符串不支持修改操作,故将单词转换成列表,元素是字符,对列表中的字符进行反转。注意res的结尾是空格,故只能返回res[:-1]。
class Solution(object):
def reverseWords(self, s):
"""
:type s: str
:rtype: str
"""
s_l = s.split(" ")
res = ""
for string in s_l:
str_cur_l = list(string)
l, r = 0, len(str_cur_l) - 1
while l < r:
str_cur_l[l], str_cur_l[r] = str_cur_l[r], str_cur_l[l]
l += 1
r -= 1
res += "".join(str_cur_l) + " "
return res[:-1]11. 盛最多水的容器
https://leetcode-cn.com/problems/container-with-most-water/
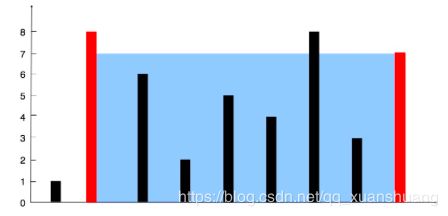
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。说明:你不能倾斜容器,且 n 的值至少为 2。
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:输入: [1,8,6,2,5,4,8,3,7],输出: 49
思路
一:双指针法,其思路是,形成的区域面积会受到其中较短那条线段长度的限制。此外,两线段距离越远,得到的面积就越大。所以我们用两个指针,一个放在开始,一个置于末尾。 使用变量capacity来持续存储到目前为止所获得的最大面积。 在每一步中,找出指针所指向的两条线段形成的区域,更新 capacity,并将指向较短线段的指针向较长线段那端移动一步。leetcode官方题解的动画做的很赞,附上链接 https://leetcode-cn.com/problems/container-with-most-water/solution/sheng-zui-duo-shui-de-rong-qi-by-leetcode/。
class Solution(object):
def maxArea(self, height):
"""
:type height: List[int]
:rtype: int
"""
capacity = 0
l, r = 0, len(height) - 1
while l < r:
h = min(height[l], height[r])
capacity = max(capacity, h * (r - l))
if height[l] < height[r]:
l += 1
else:
r -= 1
return capacity209. 长度最小的子数组
https://leetcode-cn.com/problems/minimum-size-subarray-sum/solution/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode/
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
示例: 输入: s = 7, nums = [2,3,1,2,4,3],输出: 2,解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
进阶:如果你已经完成了O(n) 时间复杂度的解法, 请尝试 O(n log n) 时间复杂度的解法。
思路
一:滑动窗口,注意到题目中的正整数的限制,维护[l,r]中的数据的累加和cur_sum大于等s,初始状态区间中没有数据,故r取-1。
若cur_sum小于s,则将r+1的元素累加进来,且r向右移动;
若cur_sum大于等于s,则将l元素从cur_sum减去,l向右移动;
若cur_sum大于等于s,更新res。
此处,res的初值必须比列表的长度大,因为存在没有符合条件的字数组,res不会更新的情况,初值大于列表长度,在特判的时候可以判断这种情况。
class Solution(object):
def minSubArrayLen(self, s, nums):
"""
:type s: int
:type nums: List[int]
:rtype: int
"""
if not nums:
return 0
n = len(nums)
l, r, cur_sum, res = 0, -1, 0, n + 1
while l < n:
if r + 1 < n and cur_sum < s:
cur_sum += nums[r + 1]
r += 1
else:
cur_sum -= nums[l]
l += 1
if cur_sum >= s:
res = min(res, r - l + 1)
if res == n + 1:
return 0
return res
同一思路,换种写法,此解法也必须借助正整数的条件,这样可以确保r一直大于等于l,且res至少等于1。
class Solution(object):
def minSubArrayLen(self, s, nums):
if not nums:
return 0
n = len(nums)
l, cur_sum, res = 0, 0, n + 1
for r in range(n):
cur_sum += nums[r]
while cur_sum >= s:
res = min(res, r - l + 1)
cur_sum -= nums[l]
l += 1
if res == n + 1:
return 0
return res二:借助二分查找,时间复杂度O(nlgn),题目中的进阶要求。二分查找要求数组必须有序,原数组无序,但是元素均是正整数,故其和有序,且要求也是累加和相关,故可行。此处为方便,累加和的列表长度是n+1,其中sum_nums[i]表示前i个元素的累加和,即[0,i-1]的和,并且要注意nums和sum_nums的下标差1,例如sum_nums[mid + 1] - sum_nums[i]表示下标在[i,mid]之间的元素的和。
class Solution(object):
def minSubArrayLen(self, s, nums):
if not nums:
return 0
n = len(nums)
sum_nums, res = [0] * (n + 1), n + 1
for i in range(1, n + 1):
sum_nums[i] = nums[i - 1] + sum_nums[i - 1]
if sum_nums[-1] < s:
return 0
for i in range(0, n):
l, r = i, n
while l < r:
mid = l + (r - l) // 2
if sum_nums[mid + 1] - sum_nums[i]< s:
l = mid + 1
else:
r = mid
res = min(res, r - i + 1)
return res325. 和等于 k 的最长子数组长度
https://leetcode-cn.com/problems/maximum-size-subarray-sum-equals-k/
给定一个数组 nums 和一个目标值 k,找到和等于 k 的最长子数组长度。如果不存在任意一个符合要求的子数组,则返回 0。
注意: nums 数组的总和是一定在 32 位有符号整数范围之内的。
示例 1:输入: nums = [1, -1, 5, -2, 3], k = 3,输出: 4 ,解释: 子数组 [1, -1, 5, -2] 和等于 3,且长度最长。
示例 2:输入: nums = [-2, -1, 2, 1], k = 1,输出: 2 ,解释: 子数组 [-1, 2] 和等于 1,且长度最长。
进阶:你能使时间复杂度在 O(n) 内完成此题吗?
思路
一:稍微优化的暴力解,时间复杂度O(n^2),leetcode上未通过,i,j的下标是指sum_nums数组的下标,而非nums数组的下标,其中sum_nums[i]表示前i个元素的累加和,即[0, i-1]的和,sum_nums[i] - sum_nums[j]表示nums中下标在区间[j, i-1]的元素的和。
class Solution(object):
def maxSubArrayLen(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
if not nums:
return 0
res, n = 0, len(nums)
sum_nums = [0] * (n + 1)
for i in range(1, n + 1):
sum_nums[i] = sum_nums[i-1] + nums[i-1]
for i in range(0, n + 1):
for j in range(n, i, -1):
if sum_nums[j] - sum_nums[i] == k:
res = max(res, j - i)
break
return res二:借助哈希表,此处用的字典,借用字典存储第一个出现该累积和的下标,只要保存第一个出现该累积和的位置,后面再出现直接跳过(最长的子数组肯定是左边界肯定是最早出现的)。只需要一次遍历,得到累加和的数组,再用一次遍历加查表即可完成,时间复杂度O(n)。
class Solution(object):
def maxSubArrayLen(self, nums, k):
if not nums:
return 0
n = len(nums)
sum_nums, res = [0] * (n + 1), 0
for i in range(1, n + 1):
sum_nums[i] = sum_nums[i-1] + nums[i-1]
rec,rec[0] = {}, 0
for i in range(1, n + 1):
# k : sum_nums[i] - sum_nums[j],是[j, i-1]的和
item = sum_nums[i] - k
if item in rec:
res = max(res, i - rec[item])
if sum_nums[i] not in rec:
rec[sum_nums[i]] = i
return res之前还做过一点点无用功,知道只用第一次出现该值的下标,但是却存储了该值的所有下标。
from collections import defaultdict
class Solution(object):
def maxSubArrayLen(self, nums, k):
if not nums:
return 0
res, n = 0, len(nums)
sum_nums = [0] * (n + 1)
for i in range(1, n + 1):
sum_nums[i] = sum_nums[i-1] + nums[i-1]
rec = defaultdict(list)
rec[0] = [0]
for i in range(1, n + 1):
# k : sum_nums[i] - sum_nums[j],是[j, i-1]的和
item = sum_nums[i] - k
if item in rec:
res = max(res, i - rec[item][0])
rec[sum_nums[i]].append(i)
return res718. 最长重复子数组
https://leetcode-cn.com/problems/maximum-length-of-repeated-subarray/
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例 1:输入:A: [1,2,3,2,1],B: [3,2,1,4,7],输出: 3,解释: 长度最长的公共子数组是 [3, 2, 1]。说明:1 <= len(A), len(B) <= 1000,0 <= A[i], B[i] < 100
思路
一:用动态规划,dp[i][j]表示以A[i]和B[j]结尾的重复字数组的长度,此处重复子数组,是指连续子数组。
- 若A[i]=B[j],则应该在dp[i-1][j-1]的基础上加1;
- 否则,不存在以A[i]和B[j]结尾的重复字数组,dp[i][j]应该为0,不用更新。
结果,取dp数组的最大值。
class Solution(object):
def findLength(self, A, B):
"""
:type A: List[int]
:type B: List[int]
:rtype: int
"""
if not A or not B:
return 0
dp = [[0] * len(B) for _ in range(len(A))]
res = 0
for j in range(len(B)):
if B[j] == A[0]:
dp[0][j], res = 1, 1
for i in range(len(A)):
if A[i] == B[0]:
dp[i][0], res = 1, 1
for i in range(1, len(A)):
for j in range(1, len(B)):
if A[i] == B[j]:
dp[i][j] = dp[i-1][j-1] + 1
res = max(res, dp[i][j])
return res303. 区域和检索 - 数组不可变
https://leetcode-cn.com/problems/range-sum-query-immutable/
给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点。
示例:给定 nums = [-2, 0, 3, -5, 2, -1],求和函数为 sumRange()
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
说明:你可以假设数组不可变。会多次调用 sumRange 方法。
思路
一:缓存,假设数组不可变,故可以缓存累加和,多次调用sumRange 方法,则sumRange函数的时间复杂度不能高,leetcode上通常只能O(1),偶尔O(n)也行。这题经典的求某区间的累加和。
class NumArray(object):
def __init__(self, nums):
"""
:type nums: List[int]
"""
if not nums:
self.rec = None
return
self.rec = [0] * len(nums)
self.rec[0] = nums[0]
for i in range(1, len(nums)):
self.rec[i] = self.rec[i - 1] + nums[i]
def sumRange(self, i, j):
"""
:type i: int
:type j: int
:rtype: int
"""
if not self.rec:
return None
if i == 0:
return self.rec[j]
return self.rec[j] - self.rec[i - 1]
# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(i,j)304. 二维区域和检索 - 矩阵不可变
https://leetcode-cn.com/problems/range-sum-query-2d-immutable/
给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2)。

上图子矩阵左上角 (row1, col1) = (2, 1) ,右下角(row2, col2) = (4, 3),该子矩形内元素的总和为 8。
示例:
给定 matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
说明:你可以假设矩阵不可变。会多次调用 sumRegion 方法。你可以假设 row1 ≤ row2 且 col1 ≤ col2。
思路
一:仿照303题的一维区域,开辟一个二维列表,存储按行的累加和,故init是O(n^2)的时间复杂度,sumRegion因为缓存的是按行的累加和,故需要按行累加,时间复杂度O(n)。leetcode上通过了。
class NumMatrix(object):
def __init__(self, matrix):
"""
:type matrix: List[List[int]]
"""
self.flag = True
if not matrix:
self.flag = False
return
row, col = len(matrix), len(matrix[0])
self.sum_region = [[0] * (col + 1) for _ in range(row)]
for i in range(row):
for j in range(1, col + 1):
self.sum_region[i][j] = self.sum_region[i][j-1] + matrix[i][j - 1]
def sumRegion(self, row1, col1, row2, col2):
"""
:type row1: int
:type col1: int
:type row2: int
:type col2: int
:rtype: int
"""
if not self.flag:
return
res = 0
for i in range(row1, row2 + 1):
res += self.sum_region[i][col2 + 1] - self.sum_region[i][col1]
return res
# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)二:依旧是缓存,只不过缓存的方式变了。
class NumMatrix(object):
def __init__(self, matrix):
self.rec = None
if not matrix or not matrix[0]:
return self.rec
m, n = len(matrix), len(matrix[0])
self.rec = [[0] * n for _ in range(m)]
self.rec[0][0] = matrix[0][0]
for i in range(1, m):
self.rec[i][0] = self.rec[i - 1][0] + matrix[i][0]
for j in range(1, n):
self.rec[0][j] = self.rec[0][j - 1] + matrix[0][j]
for i in range(1, m):
for j in range(1, n):
self.rec[i][j] = (self.rec[i - 1][j] + self.rec[i][j - 1]
- self.rec[i - 1][j - 1] + matrix[i][j])
def sumRegion(self, row1, col1, row2, col2):
if not self.rec:
return None
if row1 == 0 and col1 == 0:
return self.rec[row2][col2]
if row1 == 0:
return self.rec[row2][col2] - self.rec[row2][col1 - 1]
if col1 == 0:
return self.rec[row2][col2] - self.rec[row1 - 1][col2]
return (self.rec[row2][col2] - self.rec[row2][col1 - 1]
- self.rec[row1 - 1][col2] + self.rec[row1 - 1][col1 - 1])
# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)3. 无重复字符的最长子串
https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:输入: "abcabcbb",输出: 3 ,解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:输入: "bbbbb",输出: 1,解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:输入: "pwwkew",输出: 3,解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。,请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
思路
一:这种连续的可以想到滑动窗口,滑动窗口必须保证两个指针l,r,必须在保证逻辑正确的情况下确保至少有一个是会移动的,这边求最长,故只要右指针到最末尾就好。最短的话考虑左指针到最后,例如209-长度最小的子数组。
class Solution(object):
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
if not s:
return 0
char = [0] * 128
l, r = 0, -1
res = 0
# [l, r] 符合要求
while r < len(s):
if r + 1 < len(s) and char[ord(s[r + 1])] == 0:
char[ord(s[r + 1])] = 1
r += 1
res = max(res, r - l + 1)
if r == len(s) - 1:
break
else:
char[ord(s[l])] -= 1
l += 1
res = max(res, r - l + 1)
return res二:滑动窗口的另一种使用姿势,上述的方法最多需要执行 2n 个步骤。事实上,它可以被进一步优化为仅需要 n 个步骤。我们可以定义字符到索引的映射,而不是使用集合来判断一个字符是否存在。 当我们找到重复的字符时,我们可以立即跳过该窗口。也就是说,如果 s[j] 在 [i,j) 范围内有与![]() 重复的字符,不需要逐渐增加 i 。 可以直接跳过[i,
重复的字符,不需要逐渐增加 i 。 可以直接跳过[i,![]() ]范围内的所有元素,并将i变为
]范围内的所有元素,并将i变为![]() +1。这里char[ord(s[r])] = r + 1,是存的下一个元素的索引,这样做便于l = max(char[ord(s[r])], l) l的取值,若s[r]不重复,则是取的l,若s[r]重复则是取的重复元素下一元素的下标,即l到r之间永不重复。
+1。这里char[ord(s[r])] = r + 1,是存的下一个元素的索引,这样做便于l = max(char[ord(s[r])], l) l的取值,若s[r]不重复,则是取的l,若s[r]重复则是取的重复元素下一元素的下标,即l到r之间永不重复。
class Solution(object):
def lengthOfLongestSubstring(self, s):
if not s:
return 0
char = [0] * 128
l, r = 0, 0
res = 0
# [l, r] 符合要求
while r < len(s):
l = max(char[ord(s[r])], l)
char[ord(s[r])] = r + 1
res = max(res, r - l + 1)
r += 1
return resfrom collections import defaultdict
class Solution(object):
def lengthOfLongestSubstring(self, s):
if not s:
return 0
res = 1
l, rec = 0, defaultdict(int)
rec[s[0]] = 1
for r in range(1, len(s)):
rec[s[r]] += 1
if rec[s[r]] == 1:
res = max(res, r - l + 1)
else:
while s[l] != s[r]:
rec[s[l]] -= 1
l += 1
rec[s[l]] -= 1
l += 1
res = max(res, r - l + 1)
return res
159. 至多包含两个不同字符的最长子串
https://leetcode-cn.com/problems/longest-substring-with-at-most-two-distinct-characters/
给定一个字符串 s ,找出 至多 包含两个不同字符的最长子串 t 。
示例 1:输入: "eceba",输出: 3,解释: t 是 "ece",长度为3。
示例 2:输入: "ccaabbb",输出: 5,解释: t 是 "aabbb",长度为5。
思路
一:借用题3-无重复字符的最长子串的思路一,只不过判断右指针是否能向右移的标准变了一下,3是下一个字符不能[l,r]的重复,此处的是下一个字符和[l,r]中加起来最多只有两个不同字符,解中通过_helper函数实现判断。
from collections import defaultdict
class Solution(object):
def lengthOfLongestSubstringTwoDistinct(self, s):
"""
:type s: str
:rtype: int
"""
if not s:
return 0
l, r, res, rec = 0, -1, 0, defaultdict(int)
while r < len(s):
if r + 1 < len(s) and self._helper(rec, s[r + 1]) <= 2:
rec[s[r + 1]] += 1
r += 1
res = max(res, r - l + 1)
if r + 1 == len(s):
break
else:
rec[s[l]] -= 1
l += 1
return res
def _helper(self, rec, val):
res = 0
for key, value in rec.items():
if value != 0:
res += 1
if rec[val] == 0:
res += 1
return res二:就是判断方式又改了,我们使用一个 字典rec ,把字符串里的字符都当做键,在窗口中的最右边的字符位置作为值。每一个时刻,这个字典包括不超过 3 个元素。res = max(res, r - l),是因为目前为止确定满足条件的是r-1,[l,r-1]之间有r-l个元素。
from collections import defaultdict
class Solution(object):
def lengthOfLongestSubstringTwoDistinct(self, s):
n = len(s)
if n < 3:
return n
l, r, res, rec = 0, 0, 0, defaultdict(int)
while r < n:
if len(rec) < 3:
rec[s[r]] = r
r += 1
if len(rec) == 3:
del_idx = min(rec.values())
del rec[s[del_idx]]
l = del_idx + 1
res = max(res, r - l)
return res