动态规划法求解TSP问题 C++

    “鸡汤惠”帮“鸭汤莹”看代码，于是翻出了自己写的动态规划法求解TSP问题，于是整理了一下。（算法思想在知识点整理的部分，这里是具体实现的代码）

问题描述：

      TSP问题是指旅行家要旅行n个城市，要求各个城市经历且仅经历一次然后回到出发城市，并要求所走的路程最短。各个城市间的距离可以用代价矩阵来表示。假设从顶点i出发，令d(i, V')表示从顶点i出发经过V'中各个顶点一次且仅一次，最后回到出发点i的最短路径长度，开始时，V'＝V－{i}，于是，TSP问题的动态规划函数为：

    d(i,V')=min{cik+d(k,V－{k})}(k∈V')      （式1）

    d(k,{})=cki(k≠i)                                     （式2）

程序清单：

#include
#include
#include
using namespace std;
#define MAX_IN 10

class Tsp
{
	private:
		int city_number;		//城市个数
		int **distance;			//城市距离矩阵
		int **process;			//求最短路径的过程矩阵
	public:
		Tsp(int city_number);		//构造函数
		void correct();			//矫正输入的城市代价矩阵
		void printCity();		//打印城市的距离矩阵
		void getShoretstDistance();	//动态规划法求最短路径
		void printProcess();		//打印过程矩阵

};

//构造函数
Tsp::Tsp(int city_num)
{
	int i=0,j=0;
	city_number=city_num;

	//初始化城市距离矩阵
	distance=new int*[city_number];
	cout<<"请输入"<>distance[i][j];
	}

	//生成过程矩阵
	process=new int*[city_number];
	for(i=0;i> (i - 1) ) & 1) == 1的真值来实现

			if(((j>>(i-1))&1)==1)
			{
				continue;
			}
			for(k=1;k>(k-1))&1)==0)
				{
					continue;
				}
				if(process[i][j]>distance[i][k]+process[k][j ^ (1 << (k - 1))])
				{
					process[i][j]=distance[i][k]+process[k][j ^ (1 << (k - 1))];				
					//cout<>city_number)
	{
       Tsp tsp(city_number);		//初始化城市代价矩阵
	   tsp.correct();					//纠正用户输入的代价矩阵
	   tsp.printCity();				//打印城市
	   tsp.getShoretstDistance();		//求出最短路径
	   tsp.printProcess();			//打印计算矩阵
	   cout<<"---------------------------------------"<

*/

部分说明：

 

   个人认为动态规划法求解TSP问题的难点在于（1）求城市（除了起点）之外的其他城市子集；（2）判断城市是否位于一个子集中。

       我遇到的问题是起初认为子集需要按照子集元素的个数从小到大需要排序，在这里花费了比较多的时间，后来发现其实没有必要去排序。

（1）关于求子集

   例如4个城市{0,1,2,3}，{1,2,3}依次为{}，{1}，{2}，{1,2}，{3}，{1,3}，{2,3}，{1,2,3}，如果用111表示城市321，则上述子集转换成二进制为0，01，10，001，100,101,110,111，十进制恰好是0,1,2,3,4,5,6,7。虽然子集{1,2}在{3}之前，但遍历子集{1,2}的过程并不会使用过程矩阵中关于3的行列，因此不需要排序。

（2）判断一个城市是否位于子集中

      判断一个城市是否在子集中，通过位运算(((x>>(i-1))&1)==1来实现，比如集合{1,3,5,6,7}表示成二进制串用1110101，其中集合里面有的数对应的位数写成1，没有的写成0。要判断第3位是不是1，就把1110101右移(3-1)位，得到11101，然后结果和00001进行&运算，如果结果是1说明第3位是1，则说明城市在子集中。

（3）填过程矩阵，以process[2][5]为例。

    process[2][5] 表示从2出发，通过｛1，3｝，最后回到起点。那么process[2][5] = min{C21 + process [1][{3}],C23 + process [3][{1}]} = min{C21 + process [1][4],C23 + process [3][1]} ;

  从2出发，要去{1,3}。先考虑去1的路，去了1集合{1,3}中只剩下{3} ,{3}对应二进制100，十进制4,所以要求的process表就是process [1][4],这个4可以通过(101)^(1)得到,(1) = 1<<(1-1);再看去3的路，去了3集合{1,3}中只剩下{1},{1}对应这1，所以要求的process表就是process [3][1],1通过(101) ^ (100)得到。(100) = 1<<(3-1)。

 

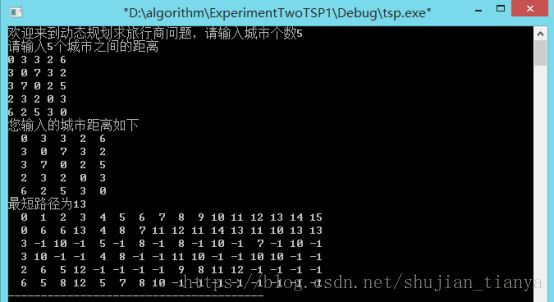
参考结果：