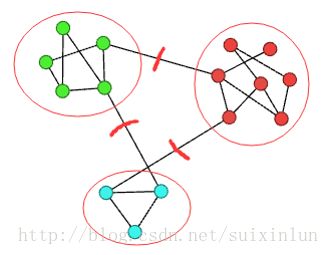
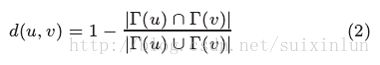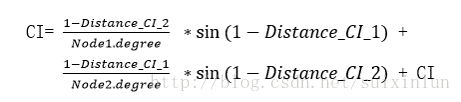Attractor算法代码整理
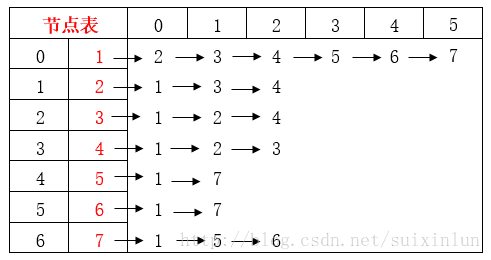
- 建立节点表
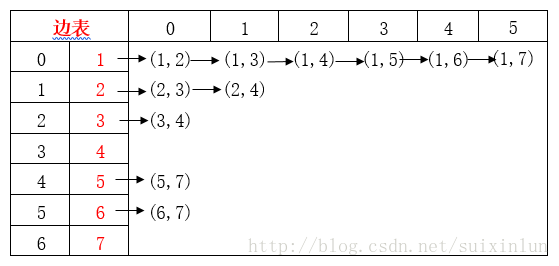
- 建立边表
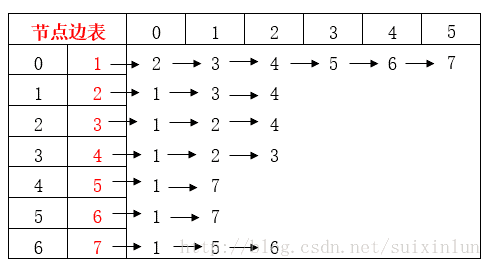
- 建立节点边表
- 交互
- 社区发现
1-3为交互做准备
一、建立节点表
EstablishNodeTable(argv[1], ator(argv[3]));参数:
argv[1]: 表示输入的数据集文件名
ator(argv[3])): 表示数据集边的数量,ator将字符串转为整型数
打开数据集文件
FILE * file = fopen(inputfilename, "r");对于每个节点i,初始其邻居节点数量为0
int NeighborNumber[NetNodeNum];
for(int i = 0; i < NetNodeNum; i++)
NeighborNumber[i] = 0;求每个节点的邻居节点数,用于为指针申请合适空间内存
for(int i=0; i"%d %d", &node_1, &node_2);
NeighborNumber[node_1-1]++;
NeighborNumber[node_2-1]++; 建立节点表
for(int i=0; i"%d %d", &node_1, &node_2);
NodeTable[node_1-1].Pointer[NodeTable[Node_1-1].NodeNum++]=node_2;
NodeTable[node_2-1].Pointer[NodeTable[Node_2-1].NodeNum++]=node_1; 为每个节点的邻居节点排序(升序)
SortFun(NodeTable[i].Pointer, NodeTable[i].NodeNum);
void SortFun(int *Pointer, int Num) 采用冒泡排序算法,但设置了“最后改变位置”来确定是否排序完毕
二、建立边表
EstablishEdgeTable();求每个节点的边数(每边只保存一次)
for(int loop_i=0; loop_i0;
for(int loop_j=0; loop_jif(NodeTable[loop_i].Pointer[loop_j]>loop_i+1)
EdgeNumber[Loop_i]++; 建立边表
int edgeid = 0; //网络总的边数
for(int loop_i=0; loop_iint edge_loc_tmp=0;//边表中每个节点的边的下标
for(int loop_j=0; loop_jif(NodeTable[loop_i].Pointer[loop_j]>loop_i+1)
{
EdgeWithAttachmentTable[loop_i].Pointer[edge_loc_tmp].n_1_ID=loop_i+1;
EdgeWithAttachmentTable[loop_i].Pointer[edge_loc_tmp].n_2_ID=NodeTable[loop_i].Pointer[loop_j];
EdgeWithAttachmentTable[loop_i].Pointer[edge_loc_tmp].e_ID=edgeid;
edge_loc_tmp++;
}
}
} 发现两个节点的共同邻居,以及各自的独有邻居
void FindNeighbors(int node_1, int node_j)
{
//变量
int num1=NodeTable[node_i-1].NodeNum;//邻居总数
int *A1=NodeTable[node_i-1].Pointer; //指向node_i的邻接表的指针
int num2=NodeTable[node_j-1].NodeNum;
int *A2=NodeTable[node_j-1].Pointer;
int p1_loc=0;//表示node_1节点的邻接表下标
int p2_loc=0;
int *p1=&A1[0];//p1指向node_i的第一个邻节点
int *p2=&A2[0];
int cn_length=0;//共同邻居(邻域)的长度
int diffa_length=0;//node_i独有邻居的长度
int diffb_length=0;
int cn_loc=1;//邻域地址下标,从1开始,0用于保存长度大小
int diffa_loc=1;
int diffb_loc=1;
while(p1_locif(A1[p1_loc]if(A1[p1_loc]!=node_j)
{
DiffA[diffa_loc]=A1[p1_loc];
diffa_length++;
diffa_loc++;
p1_loc++;
}
else
p1_loc++;
}//求node_i的独有邻居 else if(A1[p1_loc]==A2[p2_loc])
{
CN[cn_loc]=A1[p1_loc];
cn_length++;
cn_loc++;
p1_loc++;
p2_loc++;
}//求共同邻居 else
{
if(A2[p2_loc]!=node_i)
{
DiffB[diffb_loc]=A2[p2_loc];
diffb_length++;
diffb_loc++;
p2_loc++;
}
else
p2_loc++;
}//求node_j的独有邻居
}
}求剩余独有邻居
if(p1_loc==num1)
{
while(p2_locif(A2[p2_loc]!=node_i)
{
DiffB[diffb_loc]=A2[p2_loc];
diffb_length++;
diffb_loc++;
p2_loc++;
}
else
p2_loc++;
}//p2_loc余下节点为node_j的独有邻居(node_i除外)
}
else
{
while(p1_locif(A1[p1_loc]!=node_j)
{
DiffA[diffa_loc]=A1[p1_loc];
diffa_length++;
diffa_loc++;
p1_loc++;
}
else
p1_loc++;
}
}//p1_loc余下节点为node_i的独有邻居(node_j除外) 保存邻居长度
CN[0]=cn_length;
DiffA[0]=diffa_length;
DiffB[0]=diffb_length;计算每条边的杰卡德距离
EdgeWithAttachmentTable[i].Pointer[j].dist=1.0-(double)(CN[0]+2)/(double)(CN[0]+DiffA[0]+DiffB[0]+2);2为边的两端节点
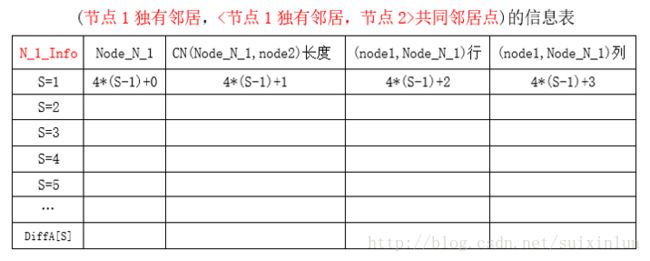
建立共同邻居的四列二维矩阵,如图:
//对于边表中第i个节点的第j条边
for(int s=1; s<=CN[0];s++)
{
int NodeCN=CN[s];
int Loc_Node_1_R=-1;//node_1和node_CN中最小节点对于id
int Loc_Node_1_C=-1;//边(node_1,node_CN)对应id(相对于最小节点)
int Loc_Node_2_R=-1;
int Loc_Node_2_C=-1;
int NodeMin=(node_1int NodeMax=(node_1>NodeCN)?node_1:NodeCN;
//求最小节点对应id
Loc_Node_1_R=NodeMin-1;
//求边所在id
for(int loop=0;loop1].EdgeNum;loop++)
if(EdgeWithAttachmentTable[NodeMin-1].Pointer[loop].n_2_ID==NodeMax)
{
Loc_Node_1_C=loop;
break;
}
//同理求Loc_Node_2_R, Loc_Node_2_C 构建二维矩阵
EdgeWithAttachmentTable[i].Pointer[j].CN_Loc[4*(s-1)+0)=Loc_Node_1_R;
EdgeWithAttachmentTable[i].Pointer[j].CN_Loc[4*(s-1)+1)=Loc_Node_1_C;
EdgeWithAttachmentTable[i].Pointer[j].CN_Loc[4*(s-1)+2)=Loc_Node_2_R;
EdgeWithAttachmentTable[i].Pointer[j].CN_Loc[4*(s-1)+3)=Loc_Node_2_C; //对于边表中第i个节点的第j条边
int Edgenum_tmp=0;//保存边(DiffA,node_2)的共同邻居总长度
for(int s=1;s<=DiffA[0];s++)
{
int Node_N_1=DiffA[s];
//求边(node_N_1,node_2)的共同邻居
FindCN(Node_N_1, node_2);
//此时,CN[0]表示Node_N_1和node_2的共同邻居长度
//求边(DiffA[s],node_2)的共同邻居总长度
Edgenum_tmp=Edgenum_tmp+CN[0];
EdgeWithAttachmentTable[i].Pointer[j].N_1_Info[4*(s-1)+0]=Node_N_1;
EdgeWithAttachmentTable[i].Pointer[j].N_1_Info[4*(s-1)+1]=CN[0];
//下述求边表中对应行列值的方法同上述共同邻居矩阵表
EdgeWithAttachmentTable[i].Pointer[j].N_1_Info[4*(s-1)+2]=NodeMin-1;
EdgeWithAttachmentTable[i].Pointer[j].N_1_Info[4*(s-1)+3]=loop;
}Edgenum_tmp=0;
for(int s=1;s<=DiffA[0];s++)
{
int Node_N_1=DiffA[1];
FindCN(Node_N_1,node_2);
//CN[0]表示Node_N_1和node_2的共同邻居长度
for(int ss=1;ss<=CN[0];ss++)
{
int NodeCN=CN[ss];
int Loc_Node_N_1_R=-1;//(Node_N_1,NodeCN)所在行
int Loc_Node_N_1_C=-1;//所在列
int Loc_Node_2_R=-1;
int Loc_Node_2_C=-1;
EdgeWithAttachmentTable[i].Pointer[j].N_1_Loc[4*Edgenum_tmp+0]=Loc_Node_N_1_R;
EdgeWithAttachmentTable[i].Pointer[j].N_1_Loc[4*Edgenum_tmp+1]=Loc_Node_N_1_C;
EdgeWithAttachmentTable[i].Pointer[j].N_1_Loc[4*Edgenum_tmp+2]=Loc_Node_2_R;
EdgeWithAttachmentTable[i].Pointer[j].N_1_Loc[4*Edgenum_tmp+3]=Loc_Node_2_C;三、建立节点边表
EstablishEdgesOfNodeTable();构建节点边表
for(int i=0;i
for(int j=0;j
{
int node_1=EdgeWithAttachmentTable[i].Pointer[j].n_1_ID;
int node_2=EdgeWithAttachmentTable[i].Pointer[j].n_2_ID;
EdgesOfNodeTable[node_1_1].Pointer[EdgesOfNodeTable[node_1-1].EdgeNum].Row=i;
EdgesOfNodeTable[node_1-1].Pointer[EdgesOfNodeTable[node_1-1].EdgeNum].Column=j;
EdgesOfNodeTable[node_1-1].EdgeNum++;
EdgesOfNodeTable[node_2-1].Pointer[EdgesOfNodeTable[node_2-1].EdgeNum].Row=i;
EdgesOfNodeTable[node_2-1].Pointer[EdgesOfNodeTable[node_2-1].EdgeNUm].Column=j;
EdgesOfNodeTable[node_2-1].EdgeNum++; 四、交互
Interaction(BETA, atoi(argv[3]));边的距离
double D[NetEdgeNum];//边的距离
int EdgeLocCount=0;//边的下标
for(int s_1=0;s_1for(int s_2=0;s_2 开始交互
int Terminate=1;//终止条件
int Loop=0;//迭代次数
while(Terminate)
{
Loop++;
for(int s_1=0;s_1for(int s_2=0;s_2if(EdgeWithAttachmentTable[s_1].Pointer[s_2].dist>0 && EdgeWithAttachmentTable[s_1].Pointer[s_2].dist<1)
{
EA ThisEA=EdgeWithAttachmentTable[s_1].Pointer[s_2];
int ThisNode_1=ThisEA.n_1_ID;
int ThisNode_2=ThisEA.n_2_ID;
int ThisEdgeId=ThisEA.e_ID;//在总边数中id
double CI=0.0;//共同邻居的影响
double N_1_I=0.0;//node_1的独有邻居影响
double N_2_I-0.0;//node_2的独有邻居影响 共同邻居影响
for(int s_3=0;s_3double Distance_CI_1;//节点1和共同邻居节点间的距离
double Distance_CI_2;//节点2和共同邻居节点间的距离
int *CNLocTmp=ThisEA.CN_Loc;//共同邻居表
Distance_CI_1=EdgeWithAttachmentTable[CNLocTmp[s_3*4+0]].Pointer[CNLocTmp[s_3*4+1]].dist;
Distance_CI_2=EdgeWithAttachmentTable[CNLocTmp[s_3*4+2]].Pointer[CNLocTmp[s_3*4+3]].dist;
int CNTmp_1=EdgeWithAttachmentTable[CNLocTmp[s_3*4+0].Pointer[CNLocTmp[s_3*4+1].n_1_ID;
int CNTmp_2=EdgeWithAttachmentTable[CNLocTmp[s_3*4+0].Pointer[CNLocTmp[s_3*4+1].n_2_ID;
int CNTmp_3=(CNTmp_1==ThisNode_1)?CNTmp_2:CNTmp_1;//表示邻居节点
CI=CI+((double)(1-Distance_CI_2)/(double)NodeTable[ThisNode_1-1].NodeNum)*sin(1-Distance_CI_1);
CI=CI+((double)(1-Distance_CI_1)/(double)NodeTable[ThisNode_2-1].NodeNum)*sin(1-Distance_CI_2);
} 节点1独有邻居影响——求lambda
int s_3=0;
int s_4=0;//节点1的所有独有邻居与节点2的共同邻居下标
int s_4_count;//当前独有邻居与节点2的共同邻居下标
while(s_3//节点1的独有邻居长度
{
int Ngh_N_1=ThisEA.N_1_Info[s_3*4+0];//节点1独有邻居
int CN_Num=ThisEA.N_1_Info[s_3*4+1];//Node_N_1和node2的共同邻居长度
double Distance_N_N_1=EdgeWithAttachmentTable[ThisEA.N_1_Info[s_3*4+2]].Pointer[ThisEA.N_1_Info[s_3*4+3]].dist;
s_4_count=s_4;
double lambda_numerator=0;//lambda的分子
//求的是当前独有邻居与共同邻居的相似度之和之和+节点2与共同邻居的相似度之和
for(s_4=s_4_count;s_4int loc_1;
int loc_2;
loc_1=ThisEA.N_1_Loc[s_4*4+0];//(Node_N_1,NodeCN)所在行
loc_2=ThisEA.N_1_Loc[s_4*4+1];//(Node_N_1,NodeCN)所在列
lambda_numerator=lambda_numerator+(1-EdgeWithAttachmentTable[loc_1].Pointer[loc_2].dist);
loc_1=ThisEA.N_1_Loc[s_4*4+2];//(node2,NodeCN)所在行
loc_2=ThisEA.N_1_Loc[s_4*4+3];//(node2,NodeCN)所在列
lambda_numerator=lambda_numerator+(1-EdgeWithAttachmentTable[loc_1].Pointer[loc_2].dist);
}
double lambda_denominator=0;//lambda的分母
//求的是当前独有邻居的所有边的相似度之和
for(int s_5=0;s_5int loc_r=EdgesOfNodeTable[Ngh_N_1].Pointer[s_5].Row;
int loc_c=EdgesOfNodeTable[Ngh_N_1].Pointer[s_5].Column;
lambda_denominator=lambda_denominator+(1-EdgeWithAttachmentTable[loc_r].Pointer[loc_c].dist);
}
double lambda=(double)lambda_numerator/(double)lambda_denominator; 节点1独有邻居影响
double parameter=(lambda>beta)?1:-1;
if(parameter==1)
N_1_I=N_1_I+parameter*lambda/(double)NodeTable[ThisNode_1-1].NodeNum*sin(1-Distance_N_N_1);
else
N_1_I=N_1_I+parameter*(beta-lambda)/(double)NodeTable[ThisNode_1-1].NodeNum*sin(1-Distance_N_N_1);
s_3++;//node1独有邻居下标
}三种交互模式总影响
D[ThisEdgeId] = D[ThisEdgeId]+(-(N_1_I+N_2_I)-(((double)1.0/(double)NodeTable[ThisNode_1-1].NodeNum+(double)1.0/(double)NodeTable[ThisNode_2-1].NodeNum)*sin(1-ThisEA.dist) +CI));
if(D[ThisEdgeId]<0)
D[ThisEdgeId]=0;
if(D[ThisEdgeId]>1)
D[ThisEdgeId]=1;
}终止迭代判断
double sum_1=0;//网络中每条边的距离之和
double sum_2=0;//更新后每条边的距离之和
int EdgeCounter=0;
for(int s_1=0;s_1for(int s_2=0;s_2if(sum_1==sum_2||Loop>1000)
Terminate=0;//结束迭代 更新距离
EdgeCounter=0;
for(int s_1=0;s_1for(int s_2=0;s_2 五、发现社区并输出结果
FindClusters(argv[2]);建立新的节点表,距离等于1的边(邻居节点)不在考虑范围内
结合队列,通过广度优先搜索算法发现簇
int clusters[NetNodeNum+1];//每个节点所在簇,cluster[0]未被使用
for(int k=0;k<=NetNodeNum;k++)
clusters[k]=-1;
int Q[NetNodeNum];//队列
int ClusterID=1;//簇的值,从1开始
int Terminate=1;//终止条件
while(Terminate){
Terminate = 0;
int id;
for(id=1; id<=NetNodeNum; id++)
if(clusters[id]==-1)
{//开始每个节点的簇均为-1,表示该节点尚未分簇
Terminate = 1;//有尚未分簇的节点便不能终止循环
clusters[id] = ClusterID;//开始,网络中第一个节点所在簇为1
Q[0] = id;//插入队列,last从-1到0
int first=-1;
int last = 0; //队尾
int v;
while(first!=last)
{ //队列不为空
v = Q[++first]; //出队列保存到v
for(int len=0; len1].NodeNum; len++) {
int RelatedNode = NodeTable_New[v-1].Pointer[len];
if(clusters[RelatedNode]==-1)
{
Q[++last] = RelatedNode; //入队列
clusters[RelatedNode] = ClusterID;
}
}
}
ClusterID = ClusterID + 1;
}
}
// 【将簇保存在二维数组】
FILE * fout = fopen(outputfile,"w");
if(fout==NULL)
printf("opening outputfile fails\n"); exit(0);
for(int i=1; i<=NetNodeNum; i++)
fprintf(fout, "%d %d\n", i, clusters[i]);//网络节点所在簇
fclose(fout);