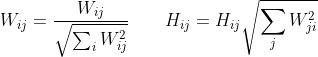Study notes for Non-negative Matrix Factorization
1. Introduction
- Non-negative matrix factorization (NMF) is a group of algorithms where V is factorized into two matrices W and H :V=WH, subjective to the non-negative constraints:Vij>=0, Wij>=0, Hij>=0; where W contains the basis vectors (of the feature space), and H is the coefficient matrix. NMF has the following properties:
- basis vectors Wi are not orthogonal, i.e., can have overlap of topics (each column, basis vector is regarded as a topic)
- can restrict W and H to be sparse
- NMF has a good interpretability
- NMF is algorithm-dependent: W and H are not unique. Because for any arbitrary invertible K x K matrix Q, we have V=WH=(WQ-1)(QV). Therefore, there could be many possible solutions, and it is important to enforce additional constraints to ensure the uniqueness of the factorization in clustering. In essence, NMF is an ill-posed problem.
- Well-posed problem refers to the problem has the properties that:
- a solution exists
- the solution is unique
- the solution's behavior hardly changes when there is a slight change in the initial conditions.
- The motivation is that features with negative values are meaningless and hard to explain in real applications
- Factorization of matrices is generally non-unique, depending on different constraints, such as PCA and vector quantization (also known as k-means, or isodata).
- PCA enforces only a weak orthogonality constraint
- Vector quantization uses a hard winner-take-all constraint
- Many different types of non-negative matrix factorization exist due to
- different cost functions for measuring the divergence between V and WH
- different regularization of the W and/or H matrices.
- A paper reading list can be found in here
- NMF is interesting because it does data clustering. In fact, NMF = Generalized K-means Clustering.
- K-means clustering = PCA
- PCA + Kmeans is a long-hold practice in dealing with high dimensional data:
- User PCA to project to low-dimension subspace
- Do K-means clustering in the subspace
- PCA guids us towards global solution, while K-means is easily trapped in local minima at high dimensions
- Cluster subspace = PCA subspace: PCA automatically projects into cluster subspace.
- PCA + Kmeans is a long-hold practice in dealing with high dimensional data:
- Many unsupervised learning methods are closely related in a simple way, including PCA, NMF, K-means, Spectral Clustering.
- NMF can be regarded as a data clustering method. Details can be referred to (Ding et al., 2005)
- K-means clustering = PCA
- NMF Summary
- NMF is doing K-means clustering (or PLSA).
- Interpretability is a key to motivate new NMF-like factorization.
- The main merits of NMF are parts-based representation and sparseness included, at the price of more complexity (Wang and Zhang, 2013).
- NMF-like algorithms can solve NP-hard combinatorial problems.
- NMF-like algorithms are extremely simple to implement.
- In conclusion, NMF is a rich paradigm for unsupervised learning and combinatorial optimization problems.
- More contents and implementations can be referred to nimfa module
2. Basic NMF Algorithm
The basic NMF algorithm is detailed in (Lee &s; Seung, 2001).
Cost Functions
Two commonly used distance measures are introduced by (Lee & Seung, 2001)
- Euclidean distance (L2 norm)
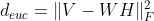
- Generalized Kullback-Leibler divergence
- The distance measure should be chosen according to the properties of the data
- Euclidean distance assumes additive Gaussian noise
- KL assumes Poisson observation model (variance scales linearly with the model)
Multiplicative Update Rules
It is known that the objective function above is not convex in W and H together. Therefore, it is unrealistic to expect an algorithm to find the global minimum. The "multiplicative update rules" are guaranteed to be non-increasing, and easy to implement and to extend.
- Euclidean distance In order to standardize while keeping the factorization unique, the resulting W and H is normalized such that the norm of each column vector is equal to one. More precisely:
- KL divergence
where
 is all-one matrix of size
is all-one matrix of size  .
.
Optimization
The currently available optimization methods are sub-optimal as they can only guarantee finding a local minimum, rather than a global minimum of the cost function. A provably optimal algorithm is unlikely in the near future as the NMF problem has been shown to generalize the k-means clustering problem which is known to be computationally difficult (NP-complete). However, as in many other data mining applications, a local minimum may still prove to be useful.
Initialize the entries in W and H with random positive values
Update W
Update H
Iterate steps 2 and 3 until loss function = 0- NMF by multiplicative update rules is implemented ===> code
- The problem is slow convergence due to a first-order convergence rate.
- Once one element of W or H becomes 0 during the iterations, it will remain 0 after that. Hence, in real implementation, we usually add a small positive epsilon to the denominator.
- NMF is not unique, depending on the initially selected values for W and H
- The initialization has a great impact on the performance of NMF. Several approaches are proposed:
- Random: non-negative random matrices
- NNDSVD: non-negative double singular value decomposition (NNDSVD) introduced in (Boutsidis and Gallopoulos, 2008). It is better for sparseness, based on two SVD processes: one approximating the data matrix, the other approximating positive sections of the resulting partial SVD factors utilizing an algebraic property of unit rank matrices.
- NNDSVDa: NNDSVD with zeros filled with the average of V. It is better when sparsity is not desired
- NNDSVDar: NNDSVD with zeros filled with small random values. It is generally faster, less accurate alternative to NNDSVDa for when sparsity is not desired.
- Many update methods are proposed to speedup the decomposition.
- Multiplicative update rules (Lee and Seung, 2001).
- Alternative Least Square.
- A state-of-the-art method is proposed by Paatero and Tapper (1994) based on alternative non-negative least square (ANLS) framework.
- Lin (2007) proposes a projected gradient method which converges faster than the multiplicative update rules. code
- Coordinate Descent.
- Cichocki and Phan (2009) propose a coordinate descend method, called FastHals, which is regarded as one of state-of-the-art methods to solve NMF.
- Hsieh and Dhillon (2011) propose a fast coordinate descend method, where Matlab codes are available via NMF-CD. This method is shown to be much faster than the FastHals method.
- Cichocki and Phan (2009) propose a coordinate descend method, called FastHals, which is regarded as one of state-of-the-art methods to solve NMF.
3. Relations with other ML Methods
NMF vs. PLSA
- Both NMF and PLSA are instances of multinomial PCA (Buntine, 2002).
- PLSA is NMF with KL-divergence (Gaussier and Goutte, 2005).
- NMF can help estimates the parameters of the PLSA model. In particular, WQ-1 corresponds to conditional probabilities while QV corresponds to joint probabilities.
- It shows that NMF works comparably with EM algorithm (Bruno and Marchand-Maillet, 2009).
- Another reference is (Ding et al., 2008)
NMF vs. kernel K-means
- NMF for clustering is equivalent to the kernel K-means algorithm (Ding et al., 2005).
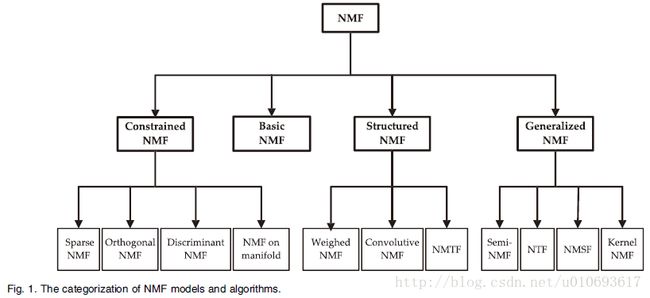
4. NMF Variants
- Wang and Zhang (2013) give an overview of the family of the NMF methods shown as follows.
- Constrained NMF approaches add regularization (penalty) terms to enforce certain constraints to NMF.
- Structured NMF approaches modify the objective function to enforce structures of data.
- Generalized NMF approaches can be regarded as deep extension to NMF.
- Hoyer (2002, 2004) introduces sparsity to NMF:
- Non-negative Sparse Coding
- NMF with Sparseness Constraints
Convex NMF
- Convex-NMF (CNMF) enhance clustering interpretation. CNMF could be reformulated as purely convex optimization, called Convex-hull non-negative matrix factorization (CHNMF). Both CNMF and CHNMF are implemented in the Python Matrix Factorization (PyMF) module (slow) and scikit-learn (sklearn) module.
- CNMF-LP is proposed by Bittorf et al. 2013
- The CNMF can be solved using a very fast, shared-memory, lock-free implementation of a SGD solver, called hottopix.
- This means we can solve very large scale problems with the same performance we have come to expect from our SVMs.
- An insightful post is worth reading via here
Local NMF (LNMF)
5. Applications in Recommender Systems
- Matrix factorization in recommender systems is reviewed in here.
- The major steps of NMF for recommendations include:
- Factorize item-user rating matrix: Rnxm=WnxrHrxm
- For the feature-user matrix H, and a specific user u whose correlation with features is defined as a column vector Hu:
- compare with other rows in Hv, and compute the euclidean distance between Hu and Hv
- find the top K users with the minimum distances, those users are used as candidates of nearest neighbors (KNN)
- adopt Pearson correlation coefficient to compute user similarity and generate predictions
- Note that it also can be used to find similar items.
- Hence, the major use of NMF is to cluster users based on the latent features, essentially it is a KNN method. The difference is to use matrix factorization to reduce dimensionality.
- Example: topic extraction with NMF
Incomplete Ratings
- The difficulty to apply NMF to recommender systems lies in that the matrix V is not complete. To address this problem, two approaches are proposed in (Zhang et al., 2006).
- EM algorithm: each step needs to execute NMF algorithm, hence really expensive.
- Weighted NMF (WNMF): only compute the cost function on the entries where the original ratings exist.
- The results show that EM-based NMF achieves better performance than WNMF at the cost of execution time.
- NMF-based approaches work better than SVD.
- A hybrid approach by mixing the EM and Weighted NMF is proposed as a compromise.
Online NMF
- It is developed for real-time data analysis in an online context, proposed by Cao et al. (2007).
- In the past, NMF is only used for static data analysis and pattern recognition due to the time and memory expensive nature.
- Online NMF is proposed to perform rapid NMF analysis to produce real-time recommendations.
- Online NMF (Cao et al., 2007)
- Incrementally update W and H using new coming data and previously trained H.
- Imposing an orthogonality constraint on H, alleviating the partial-data (i.e., data sparsity) problem.
- Incrementally update W and H using new coming data and previously trained H.
Paper list
- Gu et al., Collaborative Filtering: Weighted Nonnegative Matrix Factorization Incorporating User and Item Graphs, SDM 2010.
Online NMF Pseudocodes
time step 0: initialization; using current data V to calculate W and H by orthogonal NMF.
time step t:
using the new data U and H, calculate W' and H' via orthogonal NMF;
update W and H by W' and H' using online NMF;
time step T: output final W and H.References
- Bittorf et al., 2013, Factoring nonnegative matrices with linear programs.
- Bruno and Marchand-Maillet, 2009, Multiview clustering: A late fusion approach using latent models, SIGIR.
- Buntine, 2002, Variational extensions to EM and multinomial PCA, ECML.
- Cao et al., 2007, Detect and Track Latent Factors with Online Nonnegative Matrix Factorization.
- Cichocki and Phan, 2009, Fast local algorithms for large scale nonnegative matrix and tensor factorizations.
- Hsieh and Dhillon, 2011, Fast Coordinate Descent Methods with Variable Selection for Non-negative Matrix Factorization, KDD.
- Ding et al., 2005, On the equivalence of nonnegative matrix factorization and spectral clustering, SDM.
- Ding et al., 2008, On the equivalence between non-negative matrix factorization and probabilistic latent semantic indexing.
- Gaussier and Goutte, 2005, Relation between PLSA and NMF and implications, SIGIR.
- Lee and Seung, 2001, Algorithms for Non-negative Matrix Factorization.
- Li et al., 2001, Learning spatially localized, parts-based representation. CVPR.
- Liu et al., 2010, Distributed nonnegative matrix factorization for web-scale dyadic data analysis on MapReduce, WWW.
- Paatero and Tapper, 1994, Positive matrix factorization: A non-negative factor model with optimal utilization of error.
- Wang and Zhang, 2013, Nonnegative matrix factorization: A comprehensive review, TKDE.
- Zhang et al., 2006, Learning from incomplete ratings using non-negative matrix factorization, SIAM.