基于遗传算法二维下料问题/矩形件排样/matlab程序
基于遗传算法的二维板材切割下料优化问题/matlab程序
关键词: 遗传算法, 二维板材切割, matlab
引言
二维板材切割问题在实际的工程中有很多的应用,该问题基本等同于矩形件优化排样,具体是指将若干尺寸不相同的矩形零件在给定的矩形板材上以最优的方式排布,要求所有待排零件都必须排放在板材内,且各个零件之间不发生重叠,并满足一定的工艺要求.排样问题普遍存在于工程领域中,如钣金下料、玻璃切割、造船、车辆、家具生产、报刊排版、服装和皮革裁剪等.最优的排样方案可以最大限度地节约材料、提高材料利用率,在经济上制造可观的效益.排样问题属于典型的组合优化问题,从理论上讲,该类问题属于具有最高计算复杂性的优化计算问题,即 NP完全问题.对于 NP完全问题,以目前计算理论和方法,在可行的时间界限内不可能找到问题的最优解,只能求其局部最优的近似解.
遗传算法是一种全局随机搜索算法,它借鉴了生物界的自然选择思想和自然遗传机制,将问题的可行解构成种群,把每一个可能的解看作种群的个体,算法运行时在整个解空间里随机搜索,并按一定的评估策略(或适应度函数)对每一个个体做出评价,然后不断地使用选择、交叉、变异3个遗传算子来进化问题的解,直至产生最优解.其优点是:强调概率转移规则,具有快速随机的全局搜索能力,鲁棒性强.缺点是:对于系统中的反馈信息利用不够,当求解到一定范围时往往做大量的冗余迭代,求解效率低。
本文采用遗传算法对二维板材切割/矩形件优化排样问题进行优化求解
遗传算法实现
遗传算法设计如下:
- 编码:采用十进制整数编码方式.
- 适应度函数:将适应度函数定义为f® = Area / Area1,
其中,Area是待排入矩形零件的面积总和,Area1是所得排样图高度轮廓线以下的矩形板材面积. - 初始种群:使用随机函数来生成一定数量的十进制整数序列组成父辈群体,设定种群规模 M=50.
- 交叉算子:采用单点交叉和双点交叉
.设置交叉概率pc=1,单点交叉与双点交叉各占一半. - 变异算子:采用位置变异和旋转变异
.设置位置变异概率pm1=0.1和旋转变异概率pm2=0.1. - 选择算子:根据适应度函数值从大到小排列执行完交叉、变异操作的个体,选择前 M 个个体组成下
一代父辈群体. - 结 束 条 件:设置迭代多少代.设置maxgen = 200.
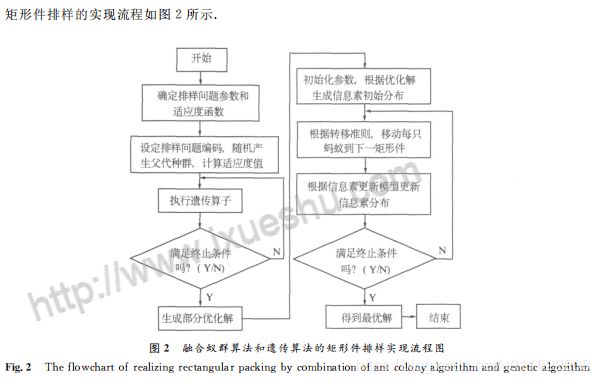
流程图
算例
在一块高10m,宽度没有没有限制的板材上,切割出一定数量的以下两种规格的零件,并使所消耗的板材的宽度最小,或容积利用率最大。
- 零件1:高度1m,宽度2m,个数10
- 零件2:高度1.5m,宽度2.5m,个数30
Matlab程序
% Author: 怡宝2号 博士猿工作室
% 淘宝链接: https://shop437222340.taobao.com/index.htm?spm=2013.1.w5002-16262391244.6.733e1fb4LF2f58
% Use: 用遗传求解二维板材物料切割问题
% 物料参数视自己的具体情况而定。
% Illustrate:输入变量(must):
% initial:零件的相关信息
% parameter:板材参数
%
% Can—changed parameter:
% Option:遗传算法的相关参数
% Option.NIND:蚁群的规模
% Option.MAXGEN:蚁群的最大迭代代数
%
% 输出: bestpop:最短路程对应的路径
% trace :最短路程
% remark:如有疑问请咨询qq:778961303
clc
clear all
close all
format compact
%遗传算法参数:NIND/种群规模;MAXGEN/最大迭代代数;PC/交叉概率;PM/变异概率;GGAP/遗传代沟
Option = struct('NIND',60, 'MAXGEN', 200, 'PC', 0.85, 'PM', 0.1, 'GGAP', 0.8);
Option.w1 = 1; Option.w2 = 0; %多目标时每个目标函数的比重//没有用到
%导入数据
[initial, parameter] = initialFunc();
%初始化种群
chrom = initialpop( Option.NIND, initial);
% 画出各客户的初始坐标
figure();
Initial_Draw_( chrom(1:2,:), parameter, initial );
%结果记录的结构体
Result = struct('mintrace',zeros( Option.MAXGEN,1),'bestpop',[]);
trace =Result;
%迭代开始
gen = 1;
while gen<=Option.MAXGEN
%计算目标函数
[cost, fitness] = CalculateFitness_( chrom, initial, parameter, Option);
%选择
[selch] = Select(chrom,fitness, Option.GGAP);
%随机交叉
[selch] = CrossOver(selch, Option.PC);
%交换变异
selch = ExchangeMutation_(selch, Option.PM);
%计算子代的目标函数和适应度
[selcost, selfitness] = CalculateFitness_( selch, initial, parameter, Option);
%重插入
[chrom,cost]=reins_(chrom,selch,1,1,cost,selcost); %也就是ObjVSel中个体目标函数越小则月容易被选择,按fitval和selfitval来进行选择
%结果记录
[mincost,index] = min(cost);
trace.mintrace(gen) = min(cost);
trace.bestpop(gen*2-1:gen*2,:) = chrom(index(1)*2-1:index(1)*2,:);
disp(['共迭代',num2str( Option.MAXGEN ),'次,现在为:',num2str(gen)]);
gen = gen + 1;
end
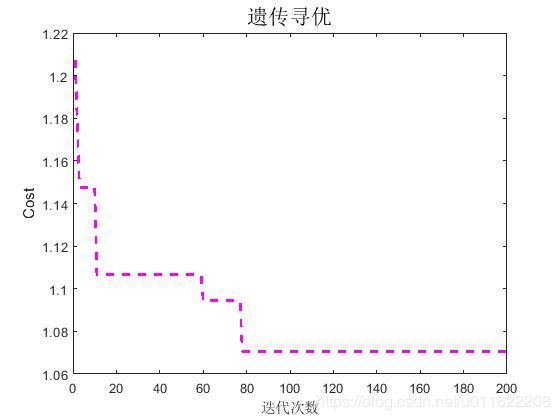
%绘制寻优迭代图
figure()
plot(trace.mintrace,'--m',...
'LineWidth',2);
grid off
xlabel('迭代次数')
ylabel('Cost')
title('遗传寻优','fontsize',16)
%显示信息
FuncDisplay(trace);
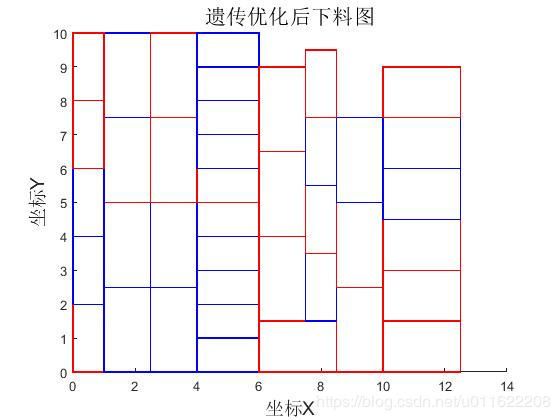
%画出最优下料图
[minvalue minindex] = min(trace.mintrace);
minchrom = trace.bestpop(minindex*2-1:minindex*2,:);
figure();
Final_Draw_( minchrom, parameter, initial );
结果
由结果可以看到,整个优化过程提高了12.785%的容积利用率。结果图如下所示:


Reference
- 融合蚁群算法和遗传算法的矩形件排样问题研究
- 矩形件排样问题的遗传算法求解
- 遗传算法求解立体仓库货位优化
- 基于遗传算法的二维板材切割下料优化问题/矩形件排样/matlab程序