Coursea-吴恩达-machine learning学习笔记（十六）【week 9之Recommender Systems】

推荐系统：
举例(预测电影评分)
用户使用 0∼5 0 ∼ 5 星给电影打分，如下图所示：

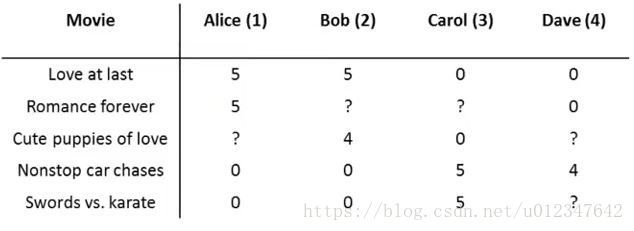
一些定义如下：
nu n u ：表示用户数量；
nm n m ：表示电影数量；
r(i,j) r ( i , j ) ：如果用户 j j 给电影 i i 打过分，则 r(i,j)=1 r ( i , j ) = 1 ；
y(i,j) y ( i , j ) ：当用户 j j 给电影 i i 打过分，即 r(i,j)=1 r ( i , j ) = 1 时，用来表示用户 j j 给电影 i i 的评分分值。

推荐系统问题就是给定 r(i,j) r ( i , j ) 和 y(i,j) y ( i , j ) ，关注所有没有评分的地方并试图预测；
推荐系统的主要工作是想出一种学习算法，能够帮助我们自动填充缺失值，试图预测用户可能感兴趣的电影，进行推荐。

第一种构建推荐系统的方法—-“基于内容的推荐”

假设每部电影有两种特征，用 x1 x 1 和 x2 x 2 表示， x1 x 1 表示这部电影属于爱情电影的程度， x2 x 2 表示这部电影属于动作电影的程度，如下图所示：

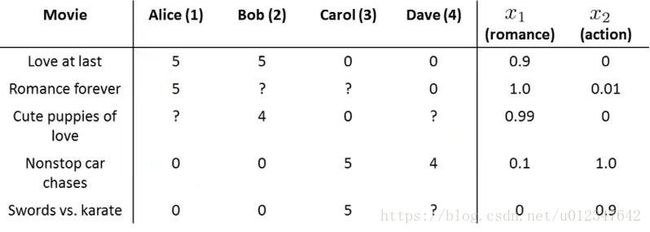
对于第一部电影来说，两个特征值分别是 0.9 0.9 和 0 0 ，加上一个特征变量 x0=1 x 0 = 1 ，则 x(1)=⎡⎣⎢10.90⎤⎦⎥ x ( 1 ) = [ 1 0.9 0 ] ， n n 表示特征变量数(不包括 x0 x 0 )，故 n=2 n = 2 ；
我们可以把每个用户的打分预测当成一个独立的线性回归问题，对于每个用户 j j ，学习参数 θ(j)∈Rn+1 θ ( j ) ∈ R n + 1 ，根据 (θ(j))Tx(i) ( θ ( j ) ) T x ( i ) 来预测用户 j j 对电影 i i 的打分。

更正式的表达：
r(i,j) r ( i , j ) ：如果用户 j j 给电影 i i 打过分，则为1，否则为0；
y(i,j) y ( i , j ) ：当 r(i,j)=1 r ( i , j ) = 1 时，表示用户 j j 给电影 i i 的评分分值；

θ(j) θ ( j ) ：表示用户 j j 的参数向量；
x(i) x ( i ) ：表示电影 i i 的特征向量。

对于用户 j j 和电影 i i ，预测评分为： (θ(j))Tx(i) ( θ ( j ) ) T x ( i ) ；
m(j) m ( j ) ：表示用户 j j 评分的电影数量；

为了学习 θ(j) θ ( j ) ，则：

minθ(j)12m(j)∑i:r(i,j)=1((θ(j))Tx(i)−y(i,j))2+λ2m(j)∑k=1n(θ(j)k)2 min θ ( j ) 1 2 m ( j ) ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 m ( j ) ∑ k = 1 n ( θ k ( j ) ) 2

去掉 1m(j) 1 m ( j ) 不影响 θ(j) θ ( j ) 的最优化结果，所以，为了学习 θ(j) θ ( j ) ，则：

J(θ(j))=minθ(j)12∑i:r(i,j)=1((θ(j))Tx(i)−y(i,j))2+λ2∑k=1n(θ(j)k)2 J ( θ ( j ) ) = min θ ( j ) 1 2 ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ k = 1 n ( θ k ( j ) ) 2

为了学习 θ(1),θ(2),⋯,θ(nu) θ ( 1 ) , θ ( 2 ) , ⋯ , θ ( n u ) ，则：

J(θ(1),⋯,θ(nu))=minθ(1),⋯,θ(nu)12∑j=1nu∑i:r(i,j)=1((θ(j))Tx(i)−y(i,j))2+λ2∑j=1nu∑k=1n(θ(j)k)2 J ( θ ( 1 ) , ⋯ , θ ( n u ) ) = min θ ( 1 ) , ⋯ , θ ( n u ) 1 2 ∑ j = 1 n u ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2

梯度下降法：

θ(j)k:=θ(j)k−α∑i:r(i,j)=1((θ(j))Tx(i)−y(i,j))x(i)k(for k=0) θ k ( j ) := θ k ( j ) − α ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) ( f o r   k = 0 )

θ(j)k:=θ(j)k−α(∑i:r(i,j)=1((θ(j))Tx(i)−y(i,j))x(i)k+λθ(j)k)(for k≠0) θ k ( j ) := θ k ( j ) − α ( ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) + λ θ k ( j ) ) ( f o r   k ≠ 0 )

注： ∂∂θ(j)kJ(θ(1),⋯,θ(nu))=∑i:r(i,j)=1((θ(j))Tx(i)−y(i,j))x(i)k+λθ(j)k ∂ ∂ θ k ( j ) J ( θ ( 1 ) , ⋯ , θ ( n u ) ) = ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) + λ θ k ( j )

第二种构建推荐系统的方法—-“协同过滤”

这种算法能自行学习所要使用的特征。
假设我们并不知道每部电影的爱情成分和动作成分，如下图：

我们采访每位用户，得到每个用户是否喜欢爱情电影和动作电影：
如： θ(1)=⎡⎣⎢050⎤⎦⎥θ(2)=⎡⎣⎢050⎤⎦⎥θ(3)=⎡⎣⎢005⎤⎦⎥θ(4)=⎡⎣⎢005⎤⎦⎥ θ ( 1 ) = [ 0 5 0 ] θ ( 2 ) = [ 0 5 0 ] θ ( 3 ) = [ 0 0 5 ] θ ( 4 ) = [ 0 0 5 ]
θ(j) θ ( j ) 可以明确告诉我们每个用户对不同题材电影的喜欢程度。

通过 θ(j) θ ( j ) 及 y(i,j) y ( i , j ) 可以推算出每部电影的特征值。
将问题标准化：
已知 θ(1),⋯,θ(nu) θ ( 1 ) , ⋯ , θ ( n u ) ，学习 x(i) x ( i ) ，使得

minx(i)12∑j:r(i,j)=1((θ(j))Tx(i)−y(i,j))2+λ2∑k=1n(x(i)k)2 min x ( i ) 1 2 ∑ j : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ k = 1 n ( x k ( i ) ) 2

已知 θ(1),⋯,θ(nu) θ ( 1 ) , ⋯ , θ ( n u ) ，学习 x(1),⋯,x(nm) x ( 1 ) , ⋯ , x ( n m ) ，使得

minx(1),⋯,x(nm)12∑i=1nm∑j:r(i,j)=1((θ(j))Tx(i)−y(i,j))2+λ2∑i=1nm∑k=1n(x(i)k)2 min x ( 1 ) , ⋯ , x ( n m ) 1 2 ∑ i = 1 n m ∑ j : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2

结合前两种方法，得到协同过滤算法的代价函数：

J(x(1),⋯,x(nm),θ(1),⋯,θ(nu))=12∑(i,j):r(i,j)=1((θ(j))Tx(i)−y(i,j))2+λ2∑i=1nm∑k=1n(x(i)k)2+λ2∑j=1nu∑k=1n(θ(j)k)2 J ( x ( 1 ) , ⋯ , x ( n m ) , θ ( 1 ) , ⋯ , θ ( n u ) ) = 1 2 ∑ ( i , j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2

算法目标为： minx(1),⋯,x(nm)θ(1),⋯,θ(nu)J(x(1),⋯,x(nm),θ(1),⋯,θ(nu)) min x ( 1 ) , ⋯ , x ( n m ) θ ( 1 ) , ⋯ , θ ( n u ) J ( x ( 1 ) , ⋯ , x ( n m ) , θ ( 1 ) , ⋯ , θ ( n u ) )
注：当用这种形式去学习特征量时，应摒弃 x0=1 x 0 = 1 和 θ0 θ 0 ， x∈Rn x ∈ R n ， θ∈Rn θ ∈ R n 。

协同过滤算法步骤：

1. 初始化 x(1),⋯,x(nm),θ(1),⋯,θ(nu) x ( 1 ) , ⋯ , x ( n m ) , θ ( 1 ) , ⋯ , θ ( n u ) 为小的随机值；
2. 用梯度下降法或其他高级优化算法，最小化代价函数( for every j=1,⋯,nu,i=1,⋯,nm f o r   e v e r y   j = 1 , ⋯ , n u , i = 1 , ⋯ , n m )
   
   x(i)k:=x(i)k−α(∑j:r(i,j)=1((θ(j))Tx(i)−y(i,j))θ(j)k+λx(i)k) x k ( i ) := x k ( i ) − α ( ∑ j : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) θ k ( j ) + λ x k ( i ) )
   θ(j)k:=θ(j)k−α(∑i:r(i,j)=1((θ(j))Tx(i)−y(i,j))x(i)k+λθ(j)k) θ k ( j ) := θ k ( j ) − α ( ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) + λ θ k ( j ) )
3. 对一个用户(参数 θ θ )和一个电影(特征值 x x )，预测评分 θTx θ T x (即 (θ(j))Tx(i) ( θ ( j ) ) T x ( i ) )

协同过滤算法的向量化方法：
有五部电影的数据集如下图：

将用户评分存储到矩阵中：
Y=⎡⎣⎢⎢⎢⎢⎢⎢55?005?4000?05500?4?⎤⎦⎥⎥⎥⎥⎥⎥ Y = [ 5 5 0 0 5 ? ? 0 ? 4 0 ? 0 0 5 4 0 0 5 ? ]
预测评分矩阵为：
⎡⎣⎢⎢⎢⎢⎢(θ(1))Tx(1)(θ(1))Tx(2)⋮(θ(1))Tx(nm)(θ(2))Tx(1)(θ(2))Tx(2)⋮(θ(2))Tx(nm)⋯⋯⋯(θ(nu))Tx(1)(θ(nu))Tx(2)⋮(θ(nu))Tx(nm)⎤⎦⎥⎥⎥⎥⎥ [ ( θ ( 1 ) ) T x ( 1 ) ( θ ( 2 ) ) T x ( 1 ) ⋯ ( θ ( n u ) ) T x ( 1 ) ( θ ( 1 ) ) T x ( 2 ) ( θ ( 2 ) ) T x ( 2 ) ⋯ ( θ ( n u ) ) T x ( 2 ) ⋮ ⋮ ⋮ ( θ ( 1 ) ) T x ( n m ) ( θ ( 2 ) ) T x ( n m ) ⋯ ( θ ( n u ) ) T x ( n m ) ]
若电影特征矩阵为 X=⎡⎣⎢⎢⎢⎢⎢(x(1))T(x(2))T⋮(x(nm))T⎤⎦⎥⎥⎥⎥⎥ X = [ ( x ( 1 ) ) T ( x ( 2 ) ) T ⋮ ( x ( n m ) ) T ] 用户参数矩阵为 Θ=⎡⎣⎢⎢⎢⎢⎢(θ(1))T(θ(2))T⋮(θ(nu))T⎤⎦⎥⎥⎥⎥⎥ Θ = [ ( θ ( 1 ) ) T ( θ ( 2 ) ) T ⋮ ( θ ( n u ) ) T ]
则预测评分矩阵为 XΘT X Θ T ，这种方法叫作低秩矩阵分解。

寻找相关电影
对于每个电影 i i ，存在特征向量 x(i)∈Rn x ( i ) ∈ R n
寻找电影 i i 的关联电影 j j ：
若 ∥x(i)−x(j)∥ ‖ x ( i ) − x ( j ) ‖ 很小 → → 电影 i i 和电影 j j 相似。

协同过滤算法实现细节：均值归一化
如下图，有一个用户没有给任何电影评分

在协同过滤算法中，目标为：

minx(1),⋯,x(nm)θ(1),⋯,θ(nu)12∑(i,j):r(i,j)=1((θ(j))Tx(i)−y(i,j))2+λ2∑i=1nm∑k=1n(x(i)k)2+λ2∑j=1nu∑k=1n(θ(j)k)2 min x ( 1 ) , ⋯ , x ( n m ) θ ( 1 ) , ⋯ , θ ( n u ) 1 2 ∑ ( i , j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2

假设 n=2 n = 2 ， θ(5)∈R2 θ ( 5 ) ∈ R 2 ，由于用户 5 5 没有对任何电影评分，所以影响 θ(5) θ ( 5 ) 的唯一项为 λ2∑k=1n(θ(5)k)2 λ 2 ∑ k = 1 n ( θ k ( 5 ) ) 2 ，为了让代价函数最小化，最终 θ(5)=[00] θ ( 5 ) = [ 0 0 ] ，所以预测用户5对电影的评分时 (θ(5))Tx(i)=0 ( θ ( 5 ) ) T x ( i ) = 0 ，其对所有电影的评分均为 0 0 ，无法推荐。

均值归一化可以解决这一情况。
Y=⎡⎣⎢⎢⎢⎢⎢⎢55?005?4000?05500?40?????⎤⎦⎥⎥⎥⎥⎥⎥ Y = [ 5 5 0 0 ? 5 ? ? 0 ? ? 4 0 ? ? 0 0 5 4 ? 0 0 5 0 ? ] 计算每个电影评分均值 μ=⎡⎣⎢⎢⎢⎢⎢⎢2.52.522.251.25⎤⎦⎥⎥⎥⎥⎥⎥ μ = [ 2.5 2.5 2 2.25 1.25 ]
令 Y=Y.−μ=⎡⎣⎢⎢⎢⎢⎢⎢2.52.5?−2.25−1.252.5?2−2.25−1.25−2.5?−22.753.75−2.5−2.5?1.75−1.25?????⎤⎦⎥⎥⎥⎥⎥⎥ Y = Y . − μ = [ 2.5 2.5 − 2.5 − 2.5 ? 2.5 ? ? − 2.5 ? ? 2 − 2 ? ? − 2.25 − 2.25 2.75 1.75 ? − 1.25 − 1.25 3.75 − 1.25 ? ] 用该矩阵学习 θ(j) θ ( j ) 和 x(i) x ( i )
用户 j j 对电影 i i 的评分预测为： (θ(j))Tx(i)+μi ( θ ( j ) ) T x ( i ) + μ i
本例中，因为 θ(5)=[00] θ ( 5 ) = [ 0 0 ] ，所以其对电影的评分为 μ=⎡⎣⎢⎢⎢⎢⎢⎢2.52.522.251.25⎤⎦⎥⎥⎥⎥⎥⎥ μ = [ 2.5 2.5 2 2.25 1.25 ]