jc2020_

【ML】李宏毅机器学习笔记

我的github链接 - 课程相关代码：

https://github.com/YidaoXianren/Machine-Learning-course-note

0. Introduction

Machine Learning: define a set of function, goodness of function, pick the best function
Regression输出的是一个标量，Classification输出的是(1)是或否(Binary Classification) (2) Multi-class Classification
选不同的function set其实就是选不同的model，model里面最简单的就是linear model;此外还有很多nonlinear model，如deep learning, SVM, decision tree, kNN...... 以上都是supervised learning - 需要搜集很多training data
Semi-supervised learning(半监督学习) - 有些有有些没有label
Transfer Learning - data not related to the task considered
Unsupervised Learning(非监督学习)
Structured Learning - Beyond Classification (输出的是一个有结构性的object)
Reinforcement Learning - 没有监督知道，只有一个好or坏的评分机制(learning from critics)
蓝色: scenario; 红色: task - 要解的问题; 绿色: method.

1. Regression

output a scalar
Step1: Model: $y = b + wx_{cp}$ w and b are parameters, w: weight, b: bias
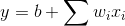
Linear Model: $y = b + \sum w_ix_i$
Step2: Goodness of Function - Loss function L: input is a function, output is how bad it is (损失函数)
first version of Loss Function: $L(f) = \sum (\hat y^n - f(x^n_{cp}))^2$ or $L(w,b) = \sum (\hat y^n - (b+wx^n_{cp}))^2$
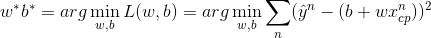
Step3: Best Function - $w^*b^* = arg \min_{w,b}L(w,b) = arg \min_{w,b}\sum_n (\hat y^n-(b+wx^n_{cp}))^2$
Gradient Descent (梯度下降法) - 只要loss func对与它的参数是可微分的就可以用，不需要一定是线性方程
- Pick an initial value ; - Compute $\frac{dL}{dw}|_{w=w^0}$ ; - $w1 \leftarrow w^0 - \eta \frac{dL}{dw}|_{w=w^0}$ , where $\eta$ is learning rate. Continue this step until finding gradient that is equal to zero.
For two parameters: ; - Pick initial value: ; - Compute $\frac{\partial L}{\partial w}|_{w=w_0, b=b_0}, \frac{\partial L}{\partial b}|_{w=w_0, b=b_0}$ ; - $w^1 \leftarrow w^0 - \eta \frac{\partial L}{\partial w}|_{w=w^0, b=b^0}$ $b^1 \leftarrow b^0 - \eta \frac{\partial L}{\partial b}|_{w=w^0, b=b^0}$ 。Continue this step until finding gradient that is equal to zero.
以上方法得出来的结果 $\theta^*$ 满足： $\theta^* = arg \min_\theta L(\theta)$
gradient descent缺点：可能会卡在saddle point或者local minima
对于linear regression, 由于它是convex的函数，所以不存在上述缺点。
Liner Regression - Gradient descent formula summary:
复杂的模型在test data上不一定有更好的表现，有可能是overfitting(过拟合)
overfit的解决方法：1. 增加input数据集 2. regularization
Regularization (正则化)
- $y = b + \sum w_ix_i$ $L = \sum_n(\hat y^n-(b + \sum w_ix_i))^2 + \lambda (w_i)^2$
- 不但要选择一个loss小的function，还要选择一个平滑的function(正则化使函数更平滑, 因为w比较小) - smoother function is more likely to be correct
- $\lambda$ 大，找出来的function就比较smooth。反之，找出来的则不太smooth. 在 $\lambda$ 由小到大变化的过程中，函数不止要考虑loss最小化还要考虑weights最小化，所以对training error最小化的考虑就会相对(于没有正则化的时候)减小，因此training error会随着 $\lambda$ 增大而增大。test error则先减小再增大。

2. Error

Bias: 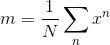$m = \frac{1}{N}\sum_nx^n$ ; Variance: $s^2 = \frac{1}{N}\sum_n(x^n-m)^2$ ; $E[s^2] = \frac{N-1}{N}\sigma^2 \neq \sigma^2$ ; want low bias & low variance
when using low degree(simple) models, variance is small, while complicate model leads to large variance. 简单的模型受采样数据的影响较小
Bias: If we average all the , it is close to $\hat f$ . 是每次训练的最佳函数(model)解(注:每次训练包含多个数据样本-sample data)，而 $\hat f$ 是真实的函数(model)。
simple models have larger bias & smaller variance, while complicate models have smaller bias & larger variance.
如果error来自于variance很大，说明现在的模型是overfitting;如果error来自bias很大，说明现在的模型是underfitting
如果模型没法fit training data，说明此时bias很大；如果模型很fit training data, 但是很不fit test data，说明此时variance很大
For large bias: add more feature, make a more complicate model
For large variance: get more data, or regularization (所有曲线都会变得比较平滑)
Cross Validation: Training Set, Validation Set, Testing Set (Public, Private)
N-fold Cross Validation - 交叉验证：可以先分成training set和validation set, train的用来训练model, validation的用来挑选model。选定model之后再用整个data set (training set+validation set)来重新train这个model的参数

3. Gradient Descent

$\theta^* = arg \min_\theta L(\theta)$ L: loss function, $\theta$ : parameters
假设 $\theta$ 有两个变量 ${\theta_1, \theta_2}$ , 则：
$\theta^0 = \left[ \begin{matrix} \theta^0_1 \\ \theta^0_2 \end{matrix} \right]$ ; $\theta^1 = \theta^0 - \eta\triangledown L(\theta^0)$ ; --> $\left[ \begin{matrix} \theta^1_1 \\ \theta^1_2 \end{matrix} \right] = \left[ \begin{matrix} \theta^0_1 \\ \theta^0_2 \end{matrix} \right] - \eta \left[ \begin{matrix} \partial L(\theta^0_1)/\partial \theta_1 \\ \partial L(\theta^0_2)/\partial \theta_2 \end{matrix} \right]$ 这里: $\triangledown L(\theta)= \left[ \begin{matrix} \partial L(\theta_1)/\partial \theta_1 \\ \partial L(\theta_2)/\partial \theta_2 \end{matrix} \right]$
设置learning rate:
- 可以绘制loss vs. No. of parameters updates(同一个循环的参数迭代次数)的曲线，观察变化趋势；
- Reduce the learning rate by some factor every few epochs - e.g. 1/t decay: $\eta^t = \eta/\sqrt{t+1}$ ；
- Give different learning rates to different parameters - Adagrad - divide the learning rate of each parameter by the root mean square of its previous derivatives
  
  $\eta^t / \sigma^t$ can be elimated... then it comes to the following form:
- Adagrad 更新法则： $w^{t+1} \leftarrow w^t - \frac{\eta}{\sqrt{\sum^t_{i=0}(g^i)^2}}g^t$ , $g^t = \frac{\partial L(\theta^t)}{\partial w}$ 为当下的梯度值(偏微分) - 造成反差效果
- The best step is $\frac{|First\ derivative|}{Second\ derivative}$ . Adagrad实际上是在模拟这样一个运算。但是又比直接算二次微分节省时间。
Stochastic Gradient Descent (让training更快):
- Gradient Descent的loss function是对全部example而言，加总的所有loss (update after seeing all examples)。而SGD是随机选一个example，然后计算这一个example的loss，然后更新参数(update for each example)
- $L^n = (\hat y^n - (b + \sum w_ix^n_i))^2$ $\theta^i = \theta^{i-1} - \eta \triangledown L^n(\theta^{i-1})$
Feature Scaling (归一化)
- 如果不做归一化，不同参数的scale不一样可能导致同样是稍微改变一个权重的大小，对于scale小的变量而言变化很小，而对于scale大的变量而言变化很大。
- 由于做update的时候是沿着等高线垂直方向更新的，归一化之后的更新效率会高一些。
- 做feature scaling:
  - for each dimension i: compute mean () and standard deviation ( $\sigma_i$ ).
  - change each data using: $x^r_i \leftarrow \frac{x^r_i - m_i}{\sigma_i}$ - after this step, the means of all dimensions are 0, and variance are all 1

可以从泰勒级数的角度理解gradient descent - learning rate够小，泰勒级数才能约等于只有一次项，才能保证每次都能往loss最小的方向移动
Gradient Descent可能不work的情况：
- Stuck at local minima
- Stuck at saddle point
- Very slow at the plateau
解析解(Analytical solution) = 封闭解(Closed-form solution): 根据严格的公式推导，给出任意自变量可以得到因变量的问题的解。数值解(Numerical solution):用数值分析，各种逼近的方法得到的近似解。

4. Classification: Probabilistic Generative Model

Generative model
- Given x, which class does it belong to:
- $P(C_1|x) = \frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$
- Estimating the probabilities from training data. Consider 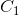as class 1, and as class 2.
- Generative Model:
- Assume the points are sampled from a Gaussian distribution
- Gaussian distribution: $f_{\mu, \Sigma}(x) = \frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}}exp\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\}$
- Input - vector x; Output - probability of sampling x. 函数的形状取决于mean ( $\mu$ ) and covariance matrix ( $\Sigma$ )
- 思路：假设examples都是在一个高斯分布中取样出来的点，通过这些点计算出mean和covariance matrix，找到这个高斯分布，再用这个高斯分布函数来计算新进来的点(是不是这一类)的概率
- 任意一个组合的mean和covariance matrix都可以表示出平面上的任意一个点，只是似然值不一样，有极大似然值(maximum likelihood)的那个就假设为这个类的高斯分布函数的参数
- Likelihood of a Gaussian with mean and covariance matrix = the probability of the Gaussian samples
  - 似然值等于所有这个类的点的概率的乘积
  - $L(\mu,\Sigma) = f_{\mu,\Sigma}(x^1)f_{\mu,\Sigma}(x^2)f_{\mu,\Sigma}(x^3)......f_{\mu,\Sigma}(x^N)$
- 拥有极大似然值的一组mean和covariance matrix为：
  - $\mu^* = \frac{1}{N}\sum^N_{n=1}x^n$ $\Sigma^* = \frac{1}{N}\sum^N_{n=1}(x^n - \mu^*)(x^n - \mu^*)^T$
- 使不同class共用同一个covariance,likelihood:
  - $L(\mu^1, \mu^2, \Sigma) = f_{\mu^1,\Sigma}(x^1)f_{\mu^1,\Sigma}(x^2)...f_{\mu^1,\Sigma}(x^{79})\times f_{\mu^2,\Sigma}(x^{80})f_{\mu^2,\Sigma}(x^{81})...f_{\mu^2,\Sigma}(x^{140})$
  - $\mu_1$ 和 $\mu_2$ 都和之前一样，分别算自己类样本的平均数。
  - $\Sigma = \frac{79}{140}\Sigma^1 + \frac{61}{140}\Sigma^2$
  - 如果用同一个covariace matrix，训练出来的boundary是线性的
Probability Distribution
- For binary features, you can use Bernoulli distributions instead.
  - If assume all dimension are independent, then it is Naive Bayes Classifier.
Posterior Probability
- 描述概率算出来的模型和logistic regression的联系，下图中在covariance matrix一致时又可以写成wx+b的形式。
- Sigmoid function形式的导出
Bayes - 先验，后验，似然
- 贝叶斯公式： P(y|x) = (P(x|y)*P(y))/P(x)
- P(y|x) 为后验概率， P(x|y)为条件概率or似然概率，P(y)和P(x)为先验概率
- 所以贝叶斯公式也可以表述为：后檐概率=（似然度*先验概率）/标准化常量。即：后验概率与先验概率和似然度的乘积成正比。

5. Logistic Regression

want to find 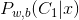$P_{w,b} (C_1|x)$ , if it is larger than or equal to 0.5, then output C1; otherwise, output C2.
Assume the data is generated based on $f_{w,b}(x) = P_{w,b}(C_1|x)$ , then the probability of generating the data is $L(w,b) = f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))...f_{w,b}(x^N)$ , where is training data. Then the most likely and is the one with largest 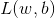: $w^*, b^* = arg \max_{w,b}L(w,b) = arg \min_{w,b} -lnL(w,b)$
$w^*, b^* = arg \min_{w,b} \sum_n-[\hat y^nlnf_{w,b}(x^n) + (1-\hat y^n)ln(1-f_{w,b}(x^n))]$ - the sum is cross entropy between two Bernoulli distribution (交叉熵).
交叉熵 - cross entropy
- assume distribution p: $p(x=1) = \hat y^n$ ; $p(x=0) = 1 - \hat y^n$
- assume distribution q: ;
- Then the cross entropy is: $H(p,q) = - \sum_xp(x)ln(q(x))$
- cross entropy实际上就是在maximize likelihood
- 注:上图的C是交叉熵
Logistic regression的step2只能用交叉熵不能用square error, 因为后者不管 $f_{w,b}(x^n)$ 等于1还是0,算出来的偏微分 $\partial L/\partial w_i$ 都等于0,无法更新。
Discriminative v.s. Generative
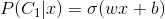
- $P(C_1|x) = \sigma(wx + b)$
- Discriminative: 直接用logistic regression的方法算出w和b
- Generative: 算出高斯分布的参数，再推导出对应的w和b (or其他概率论的方式)
- 假设不一样，所以算出来的结果是不一样的 - 在dataset一样的前提下，discriminative算出的结果准确率往往要比generative的高
  - Naive Bayes里面假设每个事件都是independent的，比如00|01|10 & 11的分类，样本不均的时候可能会分错，因为model可能会脑补不存在的情况
  - generative模型的好处：基于概率分布的假设，所需的training data比较少；对noise比较robust；Priors and class-dependent probabilities can be estimated from different sources
Multi-class Classification - Softmax (待更新 - 参数更新公式)
Limitation of Logistic Regression
- 异或问题无法直接解决 - 可以用feature transformation转成可以解决的问题(not always easy...)
- Cascading logistic regression models (把多个logistic regression堆叠起来，一些用来feature transformation,一些用来classification) - 其实就是深度学习(deep learning)

6. Deep Learning

Given network structure, define a function set.
Machine learning有一些问题不可分的时候需要做feature transformation。而deep learning就只需要设计一个structure，确定多少层，每层多少个neurons
Universality Theorem: Any continuous function f can be realized by a network with one hidden layer given enough hidden neurons

7. Backpropagation

Chain rule
Forward Pass:每个神经元输出值对输入值的偏微分 $a = \frac{\partial z}{\partial w}$
Backward Pass: 每个神经元从远端过来的偏微分 $\frac{\partial l}{\partial z}$
最后，有： $\frac{\partial l}{\partial w} = \frac{\partial z}{\partial w} \times \frac{\partial l}{\partial z} = a \times \frac{\partial l}{\partial z}$

8. Keras

例子: https://keras.io/
mnist数据集下载地址: http://yann.lecun.com/exdb/mnist/
- dense - 指的是添加的是一个fully connected的layer
- activation function: softplus, softsign, sigmoid, tanh, hard_sigmoid, linear, softmax.
- loss function: categorical crossentropy
- optimizer: adam, SGD, RMSprop, Adagrad, Adadelta, Adamax, Nadam
Mini-batch:
- 一：将全部训练集分成许多组，每组内随即分配example
- 二：随机初始化一组网络参数
- 三：选择第一组batch计算它的total loss，根据这个loss更新一次网络参数
- 四：重复步骤三直到所有的mini-batch都选择完了（完成一个步骤四称为一个epoch）
- *batch size = 1的话就相当于是Stochastic gradient descent(SGD), smaller batch size means more updates in one epoch. batch size主要是为了提速 -- 同样多的数据，大的batch size完成一次epoch需要的时间远小于小的batch size。batch size = 10 is more stable, converge faster.
- *very large batch size can yield worse performance - 很容易卡到local minima. (SGD 或者小batch size能缓解这个问题是因为每次更新时的随机batch有助于跳出gradient为0的区域)

9. Deep Neuron Networks Troubleshooting

先看看在training set上训练的结果好不好，如果结果也不好，可能是卡在了local minima等地方，要回去看看前面设置的参数；如果training结果好testing结果不好，说明是overfitting；如果两个都好，就是一个好的可以用的DNN。*区别于machine learning(SVM with rbf kernel, decision, knn with k=1), deep learning在training set不一定能得到100%准确率
Network叠很深不一定会更好，可能会有Vanishing Gradient Problem(梯度消失)的问题：接近input的几层gradient非常小，接近output的几层gradient非常大，所以当learning rate都一样的时候，前面几层的学习速度(参数更新速度)非常慢，而后面几层学习速度快很多 - 所以前面还是随机的时候(还没怎么更新)，后面的已经收敛了，因此不会在更新，卡在了一个performance很差的situation。- 该现象是来自于sigmoid function(这个activation func)，它会使input衰减，把正负无穷大的input压到0-1之间，所以当层数很多的时候就会越来越小，导致前面几层的gradient非常小。
- 解决方案1: 改成dynamic (adaptive)的learning rate
- 解决方案2: 直接改activation func为ReLU (Rectified Linear Unit)
  - 换成ReLU的原因：1. 比sigmoid计算快(没有指数运算) 2. 有生物学上的理由 3. ReLU是由无限的sigmoid叠起来形成的 4. 能够解决梯度消失的问题
  - 当用ReLU的时候，由于小于0的output都变成了0，就相当于对后面的网络没有影响，这样就只保留下了input大于0的unit和他们有链接的unit, 所以整个网络就变成了一个线性的网络(thinner linear network)，所以就没有小的gradient。 - 注：这里指的线性是局部线性(在某次input的附近范围线性)，但是整体上还是非线性的 - 分段线性。
  - 变形：Leaky ReLU; Parametric ReLU; Exponential Linear Unit (ELU)
Maxout: 每一个neuron有一个自动学出来的activation function(特指piecewise linear convex function) - 分为几段取决于把几个element放在一个group。（比如ReLU就是其中一种，两个element放一个group，所以分成了两段）
- Maxout是可以train的，当给定input的时候，我们就知道每一层里面哪个是max的值，所以可以简化成一个thin and linear的网络(只保留了max的unit)，所以用gradient descent直接算就可以了。 - 注！每个example放进来生成的简化网络是不一样的，因为每次局部的max都不一样。所以当全部example都跑完，一开始那个network的全部参数都会被训练到。
Adaptive learning rate
- Adagrad $w^{t+1} \leftarrow w^t - \frac{\eta}{\sqrt{\sum^t_{i=0}(g^i)^2}}g^t$
- RMSProp (Adagrad的变形)
- Momentum: momentum of last step minus gradient at present
  - 考虑前一次的移动方向，其实就是考虑过去所有的移动方向
- Adam: RMSProp + Momentum
- Overfitting解决方法：
  - Early Stopping:overfit的时候随着epoch的增加training的error会越来越小，但是testing的会先减小后变大，所以可以让它停在testing error最小的epoch那里(这里用validation set代替testing set)。
  - Regularization
    - Find a set of weight not only minimizing original cost(e.g. minimize square error, cross entropy) but also close to zero
    - L2 regularization
      - $L'(\theta) = L(\theta) + \lambda \frac{1}{2}\left \| \theta \right \|_2$ $\theta = {w_1, w_2, ...}$
      - L2 regularization: $\left\| \theta \right\| _2 = (w_1)^2 + (w_2)^2 + ...$ Gradient: $\frac{\partial L'}{\partial w} = \frac{\partial L}{\partial w} + \lambda w$
      - 更新规则： $w^{t+1} \leftarrow w^t - \eta (\frac{\partial L}{\partial w} + \lambda w^t) = (1-\eta \lambda)w^t - \eta \frac{\partial L}{\partial w}$
      - 第一项小于1,所以每次更新w的值都会越来越接近于0，但是由于有后面偏微分这项的存在，所以并不会最终变成0，除非是对于L影响不大的w，这些w由于影响不大，偏微分接近0，所以自然就慢慢变成了0，从而达到减少参数数量的效果。 - 所以L2 regularization也叫做weight decay。
    - L1 regularization
      - $L'(\theta) = L(\theta) + \lambda \frac{1}{2}\left \| \theta \right \|_1$ $\theta = {w_1, w_2, ...}$
      - L1 regularization: $\left\| \theta \right\| _1 = |w_1| + |w_2| + ...$ Gradient: $\frac{\partial L'}{\partial w} = \frac{\partial L}{\partial w} + \lambda sgn(w)$
      - 更新规则： $w^{t+1} \leftarrow w^t - \eta (\frac{\partial L}{\partial w} + \lambda sgn(w^t)) = w^t - \eta \frac{\partial L}{\partial w} - \eta \lambda sgn(w^t)$
      - 最后一项不管w是大于0还是小于0总是让w不断的趋近与0。
    - L1和L2正则化的比较：L2对数值大的weight的惩罚力度比较大(因为每次更新是直接消w*一个固定的值)，而L1对所有weight都一视同仁(因为每次更新消的都是sign，正负1*一个固定的值); L1做出来参数间的差距可以拉的很大，有一些会很接近于0,而L2做出来整体上比较靠近，但是很难有非常靠近0的参数。
    - Regularization在DNN中作用不是很大，因为一开始就是从接近0的地方初始化参数的。而且Regularization跟early stopping的作用有些重叠，所以有early stopping就不太需要regularization.
  - Dropout:
    - 每次在update之前: each neuron has p% to dropout - 同这些neurons链接的线也消失，使整个网络变得很thin, then using the new thinner network for training. (注！for each mini-batch, we resample the dropout neurons)
    - 在testing的时候，没有dropout。另外，如果训练的时候每个weight的dropout rate是p%，则每个weight要乘以1 - p%
    - Dropout is a kind of ensemble(训练很多种不同的network然后加权平均)
Practice - mnist:
- 如果training data不够fit，可以尝试改大hidden layer的neuron数量
- cross entropy在分类问题上比mse好很多。
- 要用GPU加速，batch size一定要开大一些才行（如10000)
- batch size从100调到10000正确率就降低了（因为相当于更新的次数少了）
- batch size从100调到1速度就会变得很慢，因为GPU不能发挥并行运算的效能
- 如果加深network的层数，会有梯度消失，performance不会变好。
- 如果把sigmoid都变成ReLU，准确率就升高了。
- 如果一开始没有做normalization，维持0-255的input区间，也无法训练成功
  - 注！要养成先看一遍training set的习惯，如笔者的数据集本身就是0-1的，再按照视频做多一次normalization就无法训练出来
- 把optimizer从SGD改成Adam可以让收敛速度更快 - 体现在accuracy变化上
- 添加了noise之后的testing data准确率不高(此时training set的准确率很高)，可以用dropout - 注！加了dropout之后在training上的performance是会变差的，但在testing set上performance会变好
- 注：Keras上每个步骤输出的acc是指在当下training的epoch的准确率

10. Convolutional Neural Network (CNN)

Why CNN for image:
- Some patterns are much smaller than the whole image: a neuron does not have to see the whole image to discover the pattern. (convolution)
- The same patterns appear in different regions. (convolution)
- Subsampling the pixels will not change the object. (max pooling)
CNN - Convolution
- Filter matrix中的data都是train出来的参数(根据training data)，但是filter matrix的size和一共有多少个filter是自己设计的。
- stride = 步长 = 每次filter移动的距离
- Filter走完生成的新的image叫做feature map
- Convolution就是fully connected的进化版 - 把每个filter中的各个元素当成一个个weight分别和每个局部图的pixel相乘。 -不过举例如果filter是3x3的就只连接9个input，不是fully connected. 并且由于整张image用的是同一个filter来卷积，相当于share weights
- 做完之后each filter is a channel
CNN - Max Pooling (下采样)
- nxn的一个范围内保留最大的一个pixel值
- 下采样也可以用average pooling
CNN - Flatten
- 把每一个channel里面的pixel值全部拉出来，拉成一个nx1的vector
- 做完以上处理之后就可以放进fully connected的network里面做gradient descent了
CNN - Example (注意参数数量)
CNN - What does CNN learn
- Degree of the activation of the k-th filter: $a^k = \sum^{11}_{i=1}\sum^{11}_{j=1}a^k_{ij}$ (assume the output of the k-th filter is a 11x11 matrix.)
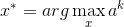
- 假设X是input图像，利用偏导 $\frac{\partial a^k}{\partial x_{ij}}$ 和gradient descent算出来的图像就是每个filter最兴奋的图像，即特征(pattern)。这里有 $x^* = arg \max_x a^k$
- DNN很容易被欺骗（如雪花噪点），可以通过增加一些额外的constraint来防止这种情况发生：
- 偏微分求出对正确class贡献最大的pixel并表示出来
- 用灰色框遮掉某一部分看是不是无法辨识出来，从而看出哪部分最有利于class判定
- 风格迁移：
  - A Neural Algorithm of Artistic Style
  - https://arxiv.org/abs/1508.06576
- Shallow(Fat+Short) v.s. Deep(Thin+Fall) - 要保证neurons数量一致才可以比较：deep的比较好
  - 在做deep的时候其实就是在做modularization(结构化,模组化的架构)，某个output class的例子太少的时候如果直接一层train会比较weak，而用modularization分类归纳就容易很多(share by following neurons as modulus) - can be trained by little data. - use previous layer as module to build classifiers.
  - 单层网络可以完成全部function，但是是很没有效率的。
  - 所以deep的可以用比较少的data和参数，也比较不容易overfitting
  - deep可以处理更复杂的问题
- 语音 - 模组化
  - Determine the state each acoustic feature belongs to
  - Gaussian Mixture Model (GMM)
  - In HMM-GMM, all the phonemes are modeled independently - not efficient.
  - DNN input - one acoustic feature; DNN output - probability of each state
- end to end learning
  - what each function should do is learned automatically
  - only provide input and output and let each layer learnt by itself - do not need to deal too much with original data, just replace them by a new layer.

11. Semi-supervised learning

semi-supervised 就是有部分训练集没有label，并且通常没有label的data比有label的多。
Trasductive learning: unlabeled data is the testing data; Inductive learning: unlabeled data is not the testing data.
semi的准确率很大程度取决于对于未知的data假设的label是否准确
Semi-supervised Learning for Generative Model
- The unlabeled data help re-estimate $P(C_1), P(C_2), \mu^1, \mu^2, \Sigma$ (可能看了unlabeled的之后知道概率分布的均值和方差在其他地方) - 进而影响decision boundary
- 算法最后总能收敛，但是怎么样初始化会影响到收敛的结果
- 类似EM算法
- 注意考虑了unlabeled data的最大似然的公式
Low-density Separation Assumption
- low-density: 在两个类的boundary附近density是最低的，数据点最少
- Self-training
  - 不能用在regression上
  - 跟generative training相似，但是Self-training用的是hard label, 而前者用的是soft label(属于两种类都可能，只是概率不一样)
  - 如果用neural network, 只能用hard label,soft label相当于反复自证，无法更新。hard label - It looks like class 1, then it is class 1.
- Entropy-based Regularization
  - Entropy of (class of an unlabeled data): evaluate how concentrate the distribution is: $E(y^u) = -\sum^5_{m=1}y^u_mln(y^u_m)$ , 要让它越小越好。（信息熵） - 这里的m指的是class
  - 所以一开始loss function只考虑labelled data的交叉熵越小越好(第一项)，现在就可以添加一项，让unlabelled data的信息熵也越小越好(第二项)： $L = \sum_{x^r}C(y^r, \hat y^r) + \lambda\sum_{x^u}E(y^u)$
- Semi-supervised SVM
  - 枚举出所有unlabelled data的分类可能，每一种都做一下svm
  - 再看那一种可能性能够让margin最大，又minimize error，又少分类错误
  - 存在一个问题是如果数据过多很难处理，需要做一些approximation
Smoothness Assumption
- Assumption: "similar" x has the same $\hat y$
- More precisely: x is not uniform, if x1 and x2 are close in a high density region, then $\hat y^1$ and $\hat y^2$ are the same.
- Cluster and then Label
- 待补充：deep auto encoder - 用来让cluster时各种类别差异更明显
- Graph-based Approach(谱聚类) - represented the data points as a graph - 如果两个点之间有相连就是一类
  - Graph Construction:
    - 首先要定义两个数据点的相似度(similarity) -
    - Add edge
      - k Nearest Neighbor(kNN)
      - e-Neighborhood: 每个点只有跟它相似度超过某个threshold的才算
    - Edge weight is proportional to
      - Gaussian Radial Basis Function (RBF): $s(x^i, x^j) = exp(-\gamma\left\|x^i-x^j\right\|^2)$
- 数据点要够多，否则有可能会传不过去
- 定量的使用方式 - 定义一个smoothness of the labels - labels有多符合假设，每个相邻data之间都用线连起来，每条线都赋予一个权重(weight)，然后smoothness表示为： $S = \frac{1}{2}\sum_{i,j}w_{i,j}(y^i-y^j)^2$ for all data, no matter labelled or not. 算出来的smoothness越小越好
  - 另一种表示方法
  - 同理，可以在原先只考虑labelled data的loss function里再加上smoothness这一项，然后gradient descent： $L = \sum_{x^r}C(y^r,\hat y^r) + \lambda S$ , 后面这项也相当于regularization.

12. Unsupervised Learning - Linear Methods (线性降维)

Clustering & Dimension Reduction (化繁为简) - only have function input; Generation(无中生有) - only have function output
Clustering
- K means
- Hierarchical Agglomerative Clustering (HAC) - 凝聚层次聚类: 分多少类取决于threshold切在哪里
Distributed Representation - 不把object定为某一类，而写成每一类百分之几
- 如果一开始某个data是很高维的，现在表示成distributed representation，就相当于降维了，dimension reduction.
Dimension Reduction - linear methods
- Feature Selection - 观察样本的数据，将没有用的dimension直接拿掉
- Principle Component Analysis (PCA) - 主成分分析 - z=Wx
  - 重要前提(假设)： $\left \| w^1 \right \|_2 = 1$
  - 希望降维之后得到的z的variance越大越好，这样可以保持data point之间的奇异度 - 才能看出区别。 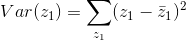$Var(z_1) = \sum_{z_1}(z_1-\bar z_1)^2$ , 这里的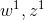表示第一维
  - 假设还想要第二维，第二维要满足 $Var(z_2) = \sum_{z_2}(z_2-\bar z_2)^2$ 且 $\left \| w^2 \right \|_2 = 1$ , 即第二维跟第一维垂直： $w^1 \cdot w^2 = 0$
  - 依次算出所需维数的z，则总的权重矩阵为各个维按顺序排列而成，且这个W是一个orthogonal matrix (因为每个row都互相垂直)
  - PCA的推导
  - SVD - 待补充
  - PCA looks like a neural network with one hidden layer (linear activation function) - autoencoder
  - PCA involves adding up and subtracting some components(images) - 如人脸的PCA是很多类似个别人脸的图像。-本质是SVD分解出来的两个matrix的值可正可负。
    - 如果非要让做出来的PCA的eigen image为可拼接笔画(或组成部分)，要用non-negative matrix factorization (NMF): 1. forcing a1, a2, ... be non-negative (can only use add when making a image by eigen images); 2. forcing w1, w2, ... be non-negative(more like "part of digits")
  - weakness of PCA
    - 由于是unsupervised的learning,有可能第一个主成分分的就刚好在两个类的boundary上，导致所有data point在这上面的投影都混在一起，无法分开。
    - 无法做non-linear dimension reduction
- Matrix Factorization （常用于推荐系统）
  - K: 潜在因素 - latent factor
  - $R^{M\times K} \cdot R^{K\times N} = R^{M \times N}$
  - 如果matrix中有一些missing data，就用gradient descent的方法做: minimizing $L = \sum_{(i,j)}(r^i \cdot r^j - n_{i,j})^2$ only considering the defined value. - Find and by gradient descent.
  - 算出和之后，就可以用来预测矩阵中缺少的值。
  - 用在文本上就叫做潜在语义分析(latent semantic analysis - LSA)
    - Number in table: term frequency(weighted by inverse document frequency)

13. Unsupervised Learning: Word Embedding （词嵌入）

即用在文字上的dimension reduction
word embedding - 表示词汇关系的vector - machine learns the meaning of words from reading a lot of documents without supervision.
1-of-N encoding: 一个很大的vector,只有一个词汇本身对应的element是1其他都是0. 缺点：词汇间关系无法从vector中表现出来
word class - 主动将词汇分成很多类并直接用类表示
word embedding: 每一个词汇都用一个continuous的vector来描述，这个vector的每个dimension都可以代表某种含义(比如会动不会动，生物非生物etc..)。
根据词汇context的上下文找vector
- Count based: If two words and 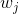frequently co-occur, and would be close to each other. 两个V的inner product正相关与两个w在同个文本中相似语义出现的次数
- Prediction-based: predict接下来要出现的词汇是哪一个词汇
- 不需要deep,一层的线性模型就可以。太多层反而不容易计算
Bag of word - 一对词汇放到一个bag里面当作一个整体
- Beyond bag of word: To understand the meaning of a word sequence, the order of the words can not be ignored.

14. Unsupervised Learning: Neighbor Embedding

Manifold Learning (流型学习)
如果在将维的过程中可以将曲面展开的话，就可以用欧几里得距离 - suitable for clustering or following supervised learning.
Locally Linear Embedding (LLE)
- 先找出一组w使得下图式子最小，然后再根据这个w找出降维后的空间，使得第二个式子也最小。

Reference:

1. https://www.bilibili.com/video/av10590361?from=search&seid=18363492564668253415

你可能感兴趣的:(【ML】李宏毅机器学习笔记)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
swagger访问路径 igotyback swagger
Swagger2.x版本访问地址：http://{ip}:{port}/{context-path}/swagger-ui.html{ip}是你的服务器IP地址。{port}是你的应用服务端口，通常为8080。{context-path}是你的应用上下文路径，如果应用部署在根路径下，则为空。Swagger3.x版本对于Swagger3.x版本（也称为OpenAPI3）访问地址：http://{ip
html 中如何使用 uniapp 的部分方法某公司摸鱼前端 html uni-app 前端
示例代码：Documentconsole.log(window);效果展示：好了，现在就可以uni.使用相关的方法了
高级编程--XML+socket练习题 masa010 java 开发语言
1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人（1）使用dom4j将信息存入xml中（2）读取信息，并打印控制台（3）添加一个city节点与子节点（4）使用socketTCP协议编写服务端与客户端，客户端输入城市ID，服务器响应相应城市信息（5）使用socketTCP协议编写服务端与客户端，客户端要求用户输入city对象，服务端接收并使用dom4j
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
四章-32-点要素的聚合彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记，使用的openlayers5.3.xapi。源码见1032.html，对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
DIV+CSS+JavaScript技术制作网页（旅游主题网页设计与制作）云南大理 STU学生网页设计网页设计期末网页作业 html静态网页 html5期末大作业网页设计 web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业：【HTML5网页期末作业(1000套)】程序员有趣的告白方式：【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面：计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript 二挡起步 web前端期末大作业 javascript html css 旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业，Web大学生网页HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
HTML网页设计制作大作业（div+css）云南我的家乡旅游景点带文字滚动二挡起步 web前端期末大作业 web设计网页规划与设计 html css javascript dreamweaver 前端
Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript：做与用户的交互行为文章目录前端学习路线
【目标检测数据集】卡车数据集1073张VOC+YOLO格式熬夜写代码的平头哥∰ 目标检测 YOLO 人工智能
数据集格式：PascalVOC格式+YOLO格式(不包含分割路径的txt文件，仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数)：1073标注数量(xml文件个数)：1073标注数量(txt文件个数)：1073标注类别数：1标注类别名称:["truck"]每个类别标注的框数：truck框数=1120总框数：1120使用标注工具：labelImg标注
钢筋长度超限检测检数据集VOC+YOLO格式215张1类别 futureflsl 数据集 YOLO 深度学习机器学习
数据集格式：PascalVOC格式+YOLO格式(不包含分割路径的txt文件，仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数)：215标注数量(xml文件个数)：215标注数量(txt文件个数)：215标注类别数：1标注类别名称:["iron"]每个类别标注的框数：iron框数=215总框数：215使用标注工具：labelImg标注规则：对类别进
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
SpringBlade dict-biz/list 接口 SQL 注入漏洞文章永久免费只为良心 oracle 数据库
SpringBladedict-biz/list接口SQL注入漏洞POC:构造请求包查看返回包你的网址/api/blade-system/dict-biz/list?updatexml(1,concat(0x7e,md5(1),0x7e),1)=1漏洞概述在SpringBlade框架中，如果dict-biz/list接口的后台处理逻辑没有正确地对用户输入进行过滤或参数化查询（PreparedSta
BART&BERT Ambition_LAO 深度学习
BART和BERT都是基于Transformer架构的预训练语言模型。模型架构：BERT(BidirectionalEncoderRepresentationsfromTransformers)主要是一个编码器（Encoder）模型，它使用了Transformer的编码器部分来处理输入的文本，并生成文本的表示。BERT特别擅长理解语言的上下文，因为它在预训练阶段使用了掩码语言模型（MLM）任务，即
spring如何整合druid连接池？惜.己 spring spring junit 数据库 java idea 后端 xml
目录spring整合druid连接池1.新建maven项目2.新建mavenModule3.导入相关依赖4.配置log4j2.xml5.配置druid.xml1)xml中如何引入properties2)下面是配置文件6.准备jdbc.propertiesJDBC配置项解释7.配置druid8.测试spring整合druid连接池1.新建maven项目打开IDE（比如IntelliJIDEA,Ecl
matlab mle 优化,MLE+: Matlab Toolbox for Integrated Modeling, Control and Optimization for Buildings... Simon Zhong matlab mle 优化
摘要：FollowingunilateralopticnervesectioninadultPVGhoodedrat,theaxonguidancecueephrin-A2isup-regulatedincaudalbutnotrostralsuperiorcolliculus(SC)andtheEphA5receptorisdown-regulatedinaxotomisedretinalgan
遥感影像的切片处理 sand&wich 计算机视觉 python 图像处理
在遥感影像分析中，经常需要将大尺寸的影像切分成小片段，以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务，如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程，同时确保每个影像片段保留正确的地理信息。准备环境首先，确保安装了必要的Python库，包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
入门MySQL——查询语法练习 K_un
前言：前面几篇文章为大家介绍了DML以及DDL语句的使用方法，本篇文章将主要讲述常用的查询语法。其实MySQL官网给出了多个示例数据库供大家实用查询，下面我们以最常用的员工示例数据库为准，详细介绍各自常用的查询语法。1.员工示例数据库导入官方文档员工示例数据库介绍及下载链接：https://dev.mysql.com/doc/employee/en/employees-installation.h
00. 这里整理了最全的爬虫框架（Java + Python）有一只柴犬爬虫系列爬虫 java python
目录1、前言2、什么是网络爬虫3、常见的爬虫框架3.1、java框架3.1.1、WebMagic3.1.2、Jsoup3.1.3、HttpClient3.1.4、Crawler4j3.1.5、HtmlUnit3.1.6、Selenium3.2、Python框架3.2.1、Scrapy3.2.2、BeautifulSoup+Requests3.2.3、Selenium3.2.4、PyQuery3.2
详解：如何设计出健壮的秒杀系统？夜空_2cd3
作者：Yrion博客园：cnblogs.com/wyq178/p/11261711.html前言：秒杀系统相信很多人见过，比如京东或者淘宝的秒杀，小米手机的秒杀。那么秒杀系统的后台是如何实现的呢？我们如何设计一个秒杀系统呢？对于秒杀系统应该考虑哪些问题？如何设计出健壮的秒杀系统？本期我们就来探讨一下这个问题：image目录一：****秒杀系统应该考虑的问题二：****秒杀系统的设计和技术方案三：*
RabbitMQ生产者重复机制与确认机制 java炒饭小能手 java-rabbitmq rabbitmq java
重复机制生产者发送消息时，出现了网络故障，导致与MQ的连接中断。为了解决这个问题，SpringAMQP提供的消息发送时的重试机制。即：当RabbitTemplate与MQ连接超时后，多次重试。需要修该发送端模块的application.yaml文件，添加下面的内容：spring:rabbitmq:connection-timeout:1s#设置MQ的连接超时时间template:retry:ena
yolov5＞onnx＞ncnn＞apk 图像处理大大大大大牛啊 opencv实战代码讲解 yolo onnx ncnn 安卓
一.yolov5pt模型转onnx条件：colabnotebookyolov51.安装环境!pipinstallonnx>=1.7.0#forONNXexport!pipinstallcoremltools==4.0#forCoreMLexport!pipinstallonnx-simplifier2.修改common.py在classFocus下面
使用由 Python 编写的 lxml 实现高性能 XML 解析 hunyxv python 笔记 python xml
转载自：文章lxml简介Python从来不出现XML库短缺的情况。从2.0版本开始，它就附带了xml.dom.minidom和相关的pulldom以及SimpleAPIforXML(SAX)模块。从2.4开始，它附带了流行的ElementTreeAPI。此外，很多第三方库可以提供更高级别的或更具有python风格的接口。尽管任何XML库都足够处理简单的DocumentObjectModel(DOM
设计模式之建造者模式(通俗易懂--代码辅助理解【Java版】） ok!ko 设计模式设计模式建造者模式 java
文章目录设计模式概述1、建造者模式2、建造者模式使用场景3、优点4、缺点5、主要角色6、代码示例：1）实现要求2）UML图3)实现步骤：1）创建一个表示食物条目和食物包装的接口2）创建实现Packing接口的实体类3）创建实现Item接口的抽象类，该类提供了默认的功能4）创建扩展了Burger和ColdDrink的实体类5）创建一个Meal类，带有上面定义的Item对象6）创建一个MealBuil
斟一小组鸡血视频和自己一起成长
http://m.v.qq.com/play/play.html?coverid=&vid=c0518henl2a&ptag=2_6.0.0.14297_copy有一种努力叫做靠自己http://m.v.qq.com/play/play.html?coverid=&vid=i0547o426g4&ptag=2_6.0.0.14297_copy世界最励志短片https://v.qq.com/x/pa
Dockerfile命令详解之 FROM 清风怎不知意容器化 java 前端 javascript
许多同学不知道Dockerfile应该如何写，不清楚Dockerfile中的指令分别有什么意义，能达到什么样的目的，接下来我将在容器化专栏中详细的为大家解释每一个指令的含义以及用法。专栏订阅传送门https://blog.csdn.net/qq_38220908/category_11989778.html指令不区分大小写。但是，按照惯例，它们应该是大写的，以便更容易地将它们与参数区分开来。(引用
《HTML 与 CSS—— 响应式设计》陈在天box html css 前端
一、引言在当今数字化时代，人们使用各种不同的设备访问互联网，包括智能手机、平板电脑、笔记本电脑和台式机等。为了确保网站在不同设备上都能提供良好的用户体验，响应式设计成为了网页开发的关键。HTML和CSS作为网页开发的基础技术，在实现响应式设计方面发挥着重要作用。本文将深入探讨HTML与CSS中的响应式设计原理、方法和最佳实践。二、响应式设计的概念与重要性（一）概念响应式设计是一种网页设计方法，旨在
【C语言】- 自定义类型：结构体、枚举、联合 Cavalier_01 C语言
【C语言】：操作符（https://mp.csdn.net/editor/html/115218055）数据类型（https://mp.csdn.net/editor/html/115219664）自定义类型：结构体、枚举、联合（https://mp.csdn.net/editor/html/115373785）变量、常量（https://mp.csdn.net/editor/html/11523
html+css网页设计旅游网站首页1个页面 html+css+js网页设计 html css 旅游
html+css网页设计旅游网站首页1个页面网页作品代码简单，可使用任意HTML辑软件（如：Dreamweaver、HBuilder、Vscode、Sublime、Webstorm、Text、Notepad++等任意html编辑软件进行运行及修改编辑等操作）。获取源码1，访问该网站https://download.csdn.net/download/qq_42431718/897527112，点击
[数据集][目标检测]汽车头部尾部检测数据集VOC+YOLO格式5319张3类别 FL1623863129 数据集目标检测汽车 YOLO
数据集制作单位：未来自主研究中心(FIRC)版权单位：未来自主研究中心(FIRC)版权声明：数据集仅仅供个人使用，不得在未授权情况下挂淘宝、咸鱼等交易网站公开售卖,由此引发的法律责任需自行承担数据集格式：PascalVOC格式+YOLO格式(不包含分割路径的txt文件，仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数)：5319标注数量(xml文件
mongodb3.03开启认证 21jhf mongodb
下载了最新mongodb3.03版本，当使用--auth 参数命令行开启mongodb用户认证时遇到很多问题，现总结如下：（百度上搜到的基本都是老版本的，看到db.addUser的就是，请忽略） Windows下我做了一个bat文件，用来启动mongodb，命令行如下： mongod --dbpath db\data --port 27017 --directoryperdb --logp
【Spark103】Task not serializable bit1129 Serializable
Task not serializable是Spark开发过程最令人头疼的问题之一，这里记录下出现这个问题的两个实例，一个是自己遇到的，另一个是stackoverflow上看到。等有时间了再仔细探究出现Task not serialiazable的各种原因以及出现问题后如何快速定位问题的所在，至少目前阶段碰到此类问题，没有什么章法 1. package spark.exampl
你所熟知的 LRU(最近最少使用) dalan_123 java
关于LRU这个名词在很多地方或听说，或使用，接下来看下lru缓存回收的实现 1、大体的想法 a、查询出最近最晚使用的项 b、给最近的使用的项做标记通过使用链表就可以完成这两个操作，关于最近最少使用的项只需要返回链表的尾部；标记最近使用的项，只需要将该项移除并放置到头部，那么难点就出现你如何能够快速在链表定位对应的该项？这时候多
Javascript 跨域周凡杨 JavaScript jsonp 跨域 cross-domain
linux下安装apache服务器 g21121 apache
安装apache 下载windows版本apache，下载地址：http://httpd.apache.org/download.cgi 1.windows下安装apache Windows下安装apache比较简单，注意选择路径和端口即可，这里就不再赘述了。 2.linux下安装apache：下载之后上传到linux的相关目录，这里指定为/home/apach
FineReport的JS编辑框和URL地址栏语法简介老A不折腾 finereport web报表报表软件语法总结
JS编辑框： 1.FineReport的js。作为一款BS产品，browser端的JavaScript是必不可少的。 FineReport中的js是已经调用了finereport.js的。大家知道，预览报表时，报表servlet会将cpt模板转为html，在这个html的head头部中会引入FineReport的js，这个finereport.js中包含了许多内置的fun
根据STATUS信息对MySQL进行优化墙头上一根草 status
mysql 查看当前正在执行的操作，即正在执行的sql语句的方法为: show processlist 命令 mysql> show global status;可以列出MySQL服务器运行各种状态值，我个人较喜欢的用法是show status like '查询值%';一、慢查询mysql> show variab
我的spring学习笔记7-Spring的Bean配置文件给Bean定义别名 aijuans Spring 3
本文介绍如何给Spring的Bean配置文件的Bean定义别名？原始的 <bean id="business" class="onlyfun.caterpillar.device.Business"> <property name="writer"> <ref b
高性能mysql 之性能剖析 annan211 性能 mysql mysql 性能剖析剖析
1 定义性能优化 mysql服务器性能，此处定义为响应时间。在解释性能优化之前，先来消除一个误解，很多人认为，性能优化就是降低cpu的利用率或者减少对资源的使用。这是一个陷阱。资源时用来消耗并用来工作的，所以有时候消耗更多的资源能够加快查询速度，保持cpu忙绿，这是必要的。很多时候发现编译进了新版本的InnoDB之后，cpu利用率上升的很厉害，这并不
主外键和索引唯一性约束百合不是茶索引唯一性约束主外键约束联机删除
目标;第一步;创建两张表用户表和文章表第二步;发表文章 1,建表; ---用户表 BlogUsers --userID唯一的 --userName --pwd --sex create
线程的调度 bijian1013 java 多线程 thread 线程的调度 java多线程
1. Java提供一个线程调度程序来监控程序中启动后进入可运行状态的所有线程。线程调度程序按照线程的优先级决定应调度哪些线程来执行。 2. 多数线程的调度是抢占式的（即我想中断程序运行就中断，不需要和将被中断的程序协商） a)
查看日志常用命令 bijian1013 linux 命令 unix
一.日志查找方法，可以用通配符查某台主机上的所有服务器grep "关键字" /wls/applogs/custom-*/error.log 二.查看日志常用命令1.grep '关键字' error.log：在error.log中搜索'关键字'2.grep -C10 '关键字' error.log：显示关键字前后10行记录3.grep '关键字' error.l
【持久化框架MyBatis3一】MyBatis版HelloWorld bit1129 helloworld
MyBatis这个系列的文章，主要参考《Java Persistence with MyBatis 3》。样例数据本文以MySQL数据库为例，建立一个STUDENTS表，插入两条数据，然后进行单表的增删改查 CREATE TABLE STUDENTS ( stud_id int(11) NOT NULL AUTO_INCREMENT,
【Hadoop十五】Hadoop Counter bit1129 hadoop
1. 只有Map任务的Map Reduce Job File System Counters FILE: Number of bytes read=3629530 FILE: Number of bytes written=98312 FILE: Number of read operations=0 FILE: Number of lar
解决Tomcat数据连接池无法释放 ronin47 tomcat 连接池　优化
近段时间，公司的检测中心报表系统(SMC)的开发人员时不时找到我，说用户老是出现无法登录的情况。前些日子因为手头上有Jboss集群的测试工作，发现用户不能登录时，都是在Tomcat中将这个项目Reload一下就好了，不过只是治标而已，因为大概几个小时之后又会再次出现无法登录的情况。今天上午，开发人员小毛又找到我，要我协助将这个问题根治一下，拖太久用户难保不投诉。简单分析了一
java-75-二叉树两结点的最低共同父结点 bylijinnan java
import java.util.LinkedList; import java.util.List; import ljn.help.*; public class BTreeLowestParentOfTwoNodes { public static void main(String[] args) { /* * node data is stored in
行业垂直搜索引擎网页抓取项目 carlwu Lucene Nutch Heritrix Solr
公司有一个搜索引擎项目，希望各路高人有空来帮忙指导，谢谢！这是详细需求：（1）通过提供的网站地址(大概100-200个网站)，网页抓取程序能不断抓取网页和其它类型的文件（如Excel、PDF、Word、ppt及zip类型），并且程序能够根据事先提供的规则，过滤掉不相干的下载内容。（2）程序能够搜索这些抓取的内容，并能对这些抓取文件按照油田名进行分类，然后放到服务器不同的目录中。
[通讯与服务]在总带宽资源没有大幅增加之前,不适宜大幅度降低资费 comsci 资源
降低通讯服务资费，就意味着有更多的用户进入，就意味着通讯服务提供商要接待和服务更多的用户，在总体运维成本没有由于技术升级而大幅下降的情况下，这种降低资费的行为将导致每个用户的平均带宽不断下降，而享受到的服务质量也在下降，这对用户和服务商都是不利的。。。。。。。。 &nbs
Java时区转换及时间格式 Cwind java
本文介绍Java API 中 Date, Calendar, TimeZone和DateFormat的使用，以及不同时区时间相互转化的方法和原理。问题描述：向处于不同时区的服务器发请求时需要考虑时区转换的问题。譬如，服务器位于东八区（北京时间，GMT+8:00），而身处东四区的用户想要查询当天的销售记录。则需把东四区的“今天”这个时间范围转换为服务器所在时区的时间范围。
readonly,只读，不可用 dashuaifu js jsp disable readOnly readOnly
readOnly 和 readonly 不同，在做js开发时一定要注意函数大小写和jsp黄线的警告！！！我就经历过这么一件事：使用readOnly在某些浏览器或同一浏览器不同版本有的可以实现“只读”功能，有的就不行，而且函数readOnly有黄线警告！！！就这样被折磨了不短时间！！！（期间使用过disable函数，但是发现disable函数之后后台接收不到前台的的数据！！！）
LABjs、RequireJS、SeaJS 介绍 dcj3sjt126com js Web
LABjs 的核心是 LAB（Loading and Blocking）：Loading 指异步并行加载，Blocking 是指同步等待执行。LABjs 通过优雅的语法（script 和 wait）实现了这两大特性，核心价值是性能优化。LABjs 是一个文件加载器。RequireJS 和 SeaJS 则是模块加载器，倡导的是一种模块化开发理念，核心价值是让 JavaScript 的模块化开发变得更
[应用结构]入口脚本 dcj3sjt126com PHP yii2
入口脚本入口脚本是应用启动流程中的第一环，一个应用（不管是网页应用还是控制台应用）只有一个入口脚本。终端用户的请求通过入口脚本实例化应用并将将请求转发到应用。 Web 应用的入口脚本必须放在终端用户能够访问的目录下，通常命名为 index.php，也可以使用 Web 服务器能定位到的其他名称。控制台应用的入口脚本一般在应用根目录下命名为 yii（后缀为.php），该文
haoop shell命令 eksliang hadoop hadoop shell
cat chgrp chmod chown copyFromLocal copyToLocal cp du dus expunge get getmerge ls lsr mkdir movefromLocal mv put rm rmr setrep stat tail test text
MultiStateView不同的状态下显示不同的界面 gundumw100 android
只要将指定的view放在该控件里面，可以该view在不同的状态下显示不同的界面，这对ListView很有用，比如加载界面，空白界面，错误界面。而且这些见面由你指定布局，非常灵活。 PS：ListView虽然可以设置一个EmptyView，但使用起来不方便，不灵活，有点累赘。 <com.kennyc.view.MultiStateView xmlns:android=&qu
jQuery实现页面内锚点平滑跳转 ini JavaScript html jquery html5 css
平时我们做导航滚动到内容都是通过锚点来做，刷的一下就直接跳到内容了，没有一丝的滚动效果，而且 url 链接最后会有“小尾巴”，就像#keleyi，今天我就介绍一款 jquery 做的滚动的特效，既可以设置滚动速度，又可以在 url 链接上没有“小尾巴”。效果体验：http://keleyi.com/keleyi/phtml/jqtexiao/37.htmHTML文件代码： &
kafka offset迁移 kane_xie kafka
在早前的kafka版本中（0.8.0），offset是被存储在zookeeper中的。到当前版本（0.8.2）为止，kafka同时支持offset存储在zookeeper和offset manager（broker）中。从官方的说明来看，未来offset的zookeeper存储将会被弃用。因此现有的基于kafka的项目如果今后计划保持更新的话，可以考虑在合适
android > 搭建 cordova 环境 mft8899 android
1 , 安装 node.js http://nodejs.org node -v 查看版本 2, 安装 npm 可以先从 https://github.com/isaacs/npm/tags 下载源码解压到
java封装的比较器，比较是否全相同，获取不同字段名字 qifeifei
非常实用的java比较器，贴上代码： import java.util.HashSet; import java.util.List; import java.util.Set; import net.sf.json.JSONArray; import net.sf.json.JSONObject; import net.sf.json.JsonConfig; i
记录一些函数用法 .Aky. 位运算 PHP 数据库函数 IP
高手们照旧忽略。想弄个全天朝IP段数据库，找了个今天最新更新的国内所有运营商IP段，copy到文件，用文件函数，字符串函数把玩下。分割出startIp和endIp这样格式写入.txt文件，直接用phpmyadmin导入.csv文件的形式导入。（生命在于折腾，也许你们觉得我傻X，直接下载人家弄好的导入不就可以，做自己的菜鸟，让别人去说吧）当然用到了ip2long()函数把字符串转为整型数
sublime text 3 rust wudixiaotie Sublime Text
1.sublime text 3 => install package => Rust 2.cd ~/.config/sublime-text-3/Packages 3.mkdir rust 4.git clone https://github.com/sp0/rust-style 5.cd rust-style 6.cargo build --release 7.ctrl

【ML】 李宏毅机器学习笔记

你可能感兴趣的:(【ML】 李宏毅机器学习笔记)

【ML】李宏毅机器学习笔记

你可能感兴趣的:(【ML】李宏毅机器学习笔记)