三维点云网络——PointNet论文解读

PointNet¹ 是斯坦福大学研究人员提出的一个点云处理网络，与先前工作的不同在于这一网络可以直接输入无序点云进行处理，而无序将数据处理成规则的3Dvoxel形式进行处理。输入点云顺序对于网络的输出结果没有影响，同时也可以处理旋转平移后的点云数据。

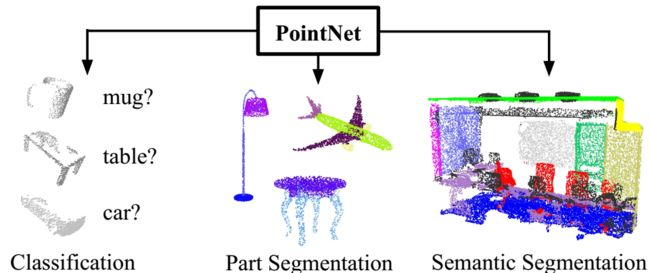
点云是一种重要的几何数据形式。卷积网络通常需要规则的数据形式作为输入，但由于点云是非规则数据类型所以通常的做法大都先对点云进行规则化的处理，将空间划分成网格的体素voxel就是一种典型的做法。但这样的方式会造成有很多不必要的体积划分使得输入数据变得稀疏，同时会影响点云数据的不变性。

PointNet从不同的角度出发来解决这一问题，考虑到点云数据的本质是一个点集，它具有一下特征：

• 无序性，点云是一个点集，没有固定的顺序；
• 与邻域点又相互作用，点云中的个体不是独立的，与周围的点具相关，具有局域特征；
• 刚体旋转、平移不变性，旋转和平移不会改变点云的分类、分割结果。

PointNet的结构十分简单，它可以直接输出点云数据，随后得到分类/分割的结果。模型对无序点云的每一个点进行独立的处理，由此来实现与输入顺序无关的点云处理。在网络中关键的结构是一个单对称函数最大池化（max pooling）。

模型通过学习选择出点云中感兴趣点/信息点，并将选择的原理编码到模型中，最后利用全连接层将学习到的特征合称为全局的描述子。

这一模型中输入点是独立的，研究人员同时增加了不依赖于数据的空间变化网络来处理刚体或仿射变换，在输入网络前对点云数据进行规范化(canonicalize)处理, 消除旋转等变换带来的影响。

---

1.处理点云通常的方法分为一下几类：

类别	方法1	方法2	方法3	方法4
点云特征	编码统计特性（不变性）	内蕴/外部特征	全局/局部特征	^ @ ^
3D数据深度学习	Volumetric（稀疏+计算量大）	Multiview多视角卷积（不易拓展）	Special空间卷积	Featurebased基于特征的卷积(受制于表达能力)
无序数据的深度学习sort规范化	序列模型RNN	对称函数集成每点信息	^ @ ^	^ @ ^

2.Framework

PointNet 利用了对称函数——最大池化的方法来对点云中各点的信息进行融合。它的具体结构如下图所示，其中输入是3通道$(x,y,z)$的点云数据, 输出是分类标签或者是分割结果。


下面让我们来看看网络的每一部分具体功能 ,网络共分为 个部分：

• 输入变换——>对齐输入点云（规范化canonical space）
• 点云处理——>MLP处理点云（升维到64）
• 特征变换——>对齐输入特征（规范化canonical space）
• 特征处理——>MLP处理特征（升维到1024）
• 对称函数处理——>全局特征（Max pooling）
• 感知机

点云变换

特征变换

max pooling

输入点云

特征: D64

特征处理: D1024

全局特征: D1024

其中第一部分的$T-Net$是一个微型网络，用于生成一个仿射变换矩阵来对点云的旋转、平移等变化进行规范化处理。这个变换/对齐网络是一个微型的PointNet，它输入原始点云数据，输出为一个$3\ast 3$的旋转矩阵：

MLP:64*128*1024

MLP:512*256

输入点云

n*1024

MaxPooling

3*3 Transform Matrix

同样的思路也可以用于对于特征空间的对齐.变换,唯一的不同在于输入编程了64维的特征，而输出则是$64\ast 64$的变换矩阵了：

MLP:64*128*1024

MLP:512*256

输入点云

n*1024

MaxPooling

64*64 Transform Matrix

第二部分则是对点云和特征进行处理的n个感知机，将$n\ast 3$的点云输入后，对于每一个点都有一个$64\ast 64$的两层感知机来对点云进行处理，这里相当于利用MLP近似了一个通用的函数，将每个点的信息通过感知机进行学习和提取，随后利用最大池化层对信息进行融合生成全局特征：
$$f(\{x_1,x_2,...,x_n\})\approx g(h(x_1),...,h(x_n)$$
其中h就相当于上面的MLP感知机，而$g$就是起到对称函数作用的Max Pooling。在网络中mlp(64,64)和mlp(64,128,1024)都是复用的，是一个MLP的n份复制。

最后，每一个输入的点都将得到1024维的描述，通过最大池化，将n-1024融合为1024维的特征来描述这一向量：

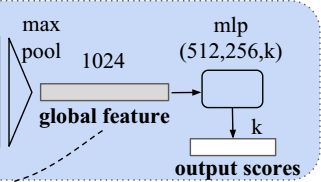
在分类任务中，点云生成的1024维特征通过最后一个MLP来进行学习，其中k是最后一层的输出数量，代表分类的类别，每个类别会对应对于点云的分类得分。

而在分割任务中，由于需要考虑局部特征，需要将n*64局域特征和1024维的全局特征结合在一起进行融合，在每一个点的64维特征后接续1024全局特征：

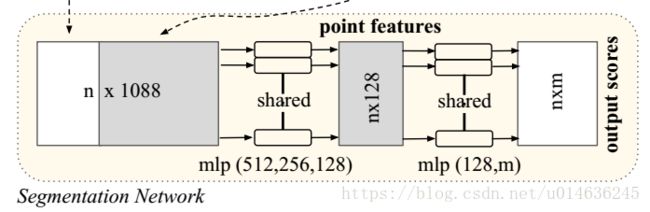
随后利用一个mlp(512,512,128)对$n\ast 1088$维的特征维度进行学习，生成$n\ast 128$的向量，再利用(128,m)的感知机对最后的特征进行分类（分割问题其实是针对每一个点的分类问题），其中n对应n个点，而m对应的是点对应的m个分类得分。

3.结果

PointNet通过上面的操作，可以得到一个稀疏的关键点集来描述总结点云所表示的形状：

上图中，第一行是原始数据、第二行树关键点集（类似于骨架）、第三行为外形的上边界。关键点集相当于定义了形状的全局特征，所有的点都将落在第二行和第三行表示之间。网络的鲁棒性就来源于此处，只要保留了关键点，及时点云有变换和扰动结果也不会受到影响。同时关键点集合也意味着可以描述整个点云的性质。

---

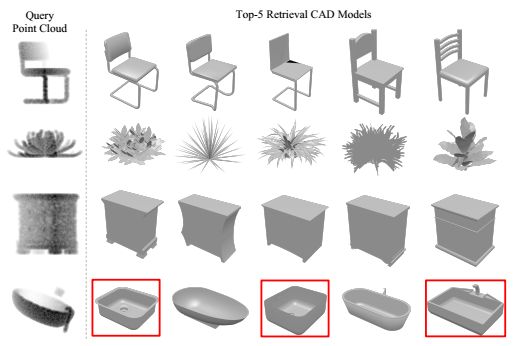
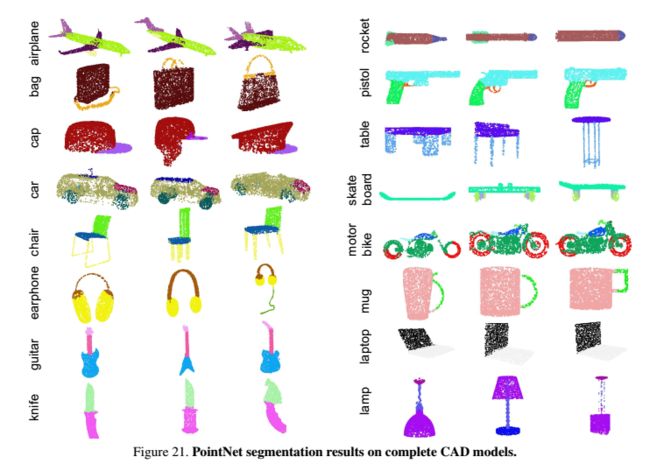
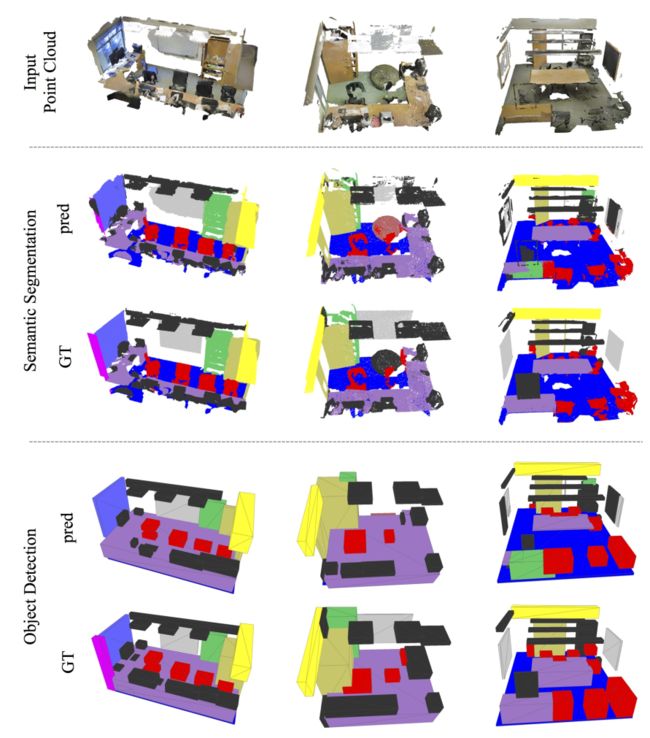
4.最后贴几个不错的结果：

1.模型检索、分割、语义分割：

5.对于点云的编码好$h(p)$

最后maxpooling输出的点云编码，可以看做是对于点云的描述。下图是对于1024个点函数在立方中进行可视化的结果，有灰度的范围描述了他们的激活区域，描述了从点云中抽取出的特征表达。

这一项目还有配套的代码, 接下来继续对代码进行学习。

》》传送门：模型及代码分析

在pointNet后，还有一个PointNet++²的工作,通过层级使用PointNet的方法，致力于解决对于局域结构和细粒度任务，主要探索了度量空间中的距离。

---

1. PointNet Project: http://stanford.edu/~rqi/pointnet/ ↩︎

2. PointNet++ Project:http://stanford.edu/~rqi/pointnet2/ ↩︎