【Machine Learning, Coursera】机器学习Week9 推荐系统笔记

ML: Recommender Systems

1. Content-based recommendations

思考：已有用户对部分电影的评价(1-5星)，且已知电影的内容构成，如何预测用户对没看过的电影的评价并作出推荐？

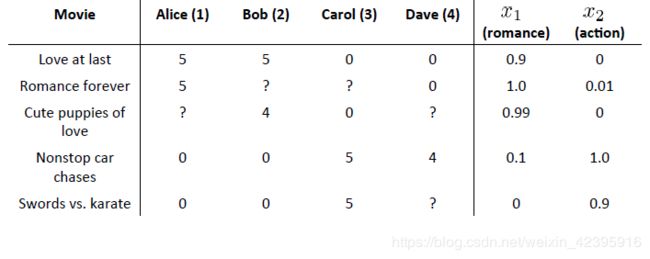
1.1 Problem formulation

首先给出一些notations:
$n_u=numberofusers$ 用户数量
$n_m=numberofmovies$ 电影数量
$r(i,j)=1ifuserjhasratedmoviei$ 用户$j$是否评价了电影$i$
$y^{(i,j)}=ratinggivenbyuserjtomoviei$ 用户$j$对电影$i$的评分，只有当 $r(i,j)=1$时有定义

$x^{(i)}=featurevectorformoviei$
电影$i$的特征向量，如$x_1$表示其爱情成分比重，$x_2$表示其动作成分比重。$x_0$为偏置项，值为1.
${\theta }^{(j)}=parametervectorforuserj$
用户$j$的参数，如${\theta }_1$表示其对爱情片的喜好程度，${\theta }_2$表示其对动作片的喜好程度。${\theta }_0$为偏置项，值为1.

对于用户$j$和电影$i$，预测其评价为$({\theta }^{(j)}{)}^T{x}^{(i)}$

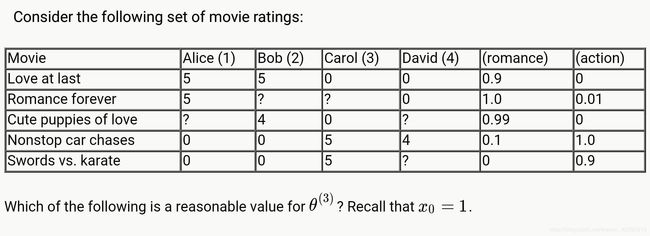
如下图中，$n_u=4$，$n_m=5$，右侧两栏是各个电影的特征。
可以看出电影1、2、3属于爱情类电影，4、5属于动作类。
观众3(Carol)对电影4和5评价很高，而对电影1和3评价很低，由此可以推断$({\theta }^{(3)}{)}^T=[0,0,5]$的可能性较高。
因此，观众3对电影2的打分可能为$({\theta }^{(3)}{)}^T{x}^{(2)}=[0,0,5]\times ([1,1,0.01]{)}^T=0.05$

1.2 Optimization objective

求某个用户的参数${\theta }^{(j)}$其实是一个基本的线性回归问题：
$$mi{n}_{{\theta }^{(j)}}\frac{1}{2m^{(j)}}\sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i.j)}{)}^2+\frac{\lambda }{2m^{(j)}}\sum _{k=1}^n({\theta }_k^{(j)}{)}^2$$
其中$m^{(j)}$为用户$j$评价过的电影数目。注意k从1开始，偏置项无需正则化。

\quad
在设计推荐系统的实践过程中，简单起见，我们会去掉$m^{(j)}$这一项，于是上式变为：
$$mi{n}_{{\theta }^{(j)}}\frac{1}{2}\sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i.j)}{)}^2+\frac{\lambda }{2}\sum _{k=1}^n({\theta }_k^{(j)}{)}^2$$

\quad
更一般地，如果要学习所有用户的参数${\theta }^{(1)},{\theta }^{(2)},....,{\theta }^{(n_u)}$，只需把$n_u$个线性回归相加：
$$mi{n}_{{\theta }^{(1)},...,{\theta }^{(n_u)}}\frac{1}{2}\sum _{j=1}^{n_u}\sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i.j)}{)}^2+\frac{\lambda }{2}\sum _{j=1}^{n_u}\sum _{k=1}^n({\theta }_k^{(j)}{)}^2$$
\quad

1.3 Optimization algorithm

$$mi{n}_{{\theta }^{(1)},...,{\theta }^{(n_u)}}\frac{1}{2}\sum _{j=1}^{n_u}\sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i.j)}{)}^2+\frac{\lambda }{2}\sum _{j=1}^{n_u}\sum _{k=1}^n({\theta }_k^{(j)}{)}^2$$

依然用梯度下降的方法求最小值，每步的更新值为：
$${\theta }_k^{(j)}:={\theta }_k^{(j)}-\alpha \sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i.j)})x_k^{(i)}(fork=0)$$
$${\theta }_k^{(j)}:={\theta }_k^{(j)}-\alpha (\sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i.j)})x_k^{(i)}+\lambda {\theta }_k^{(j)})(fork̸=0)$$
\quad

2. Collaborative Filtering

2.1 Introduction

思考：已有用户对部分电影的评价(1-5星)，且已知用户的参数${\theta }^{(1)},{\theta }^{(2)},....,{\theta }^{(n_u)}$，是不是也能反过来求$x^{(i)}$呢？

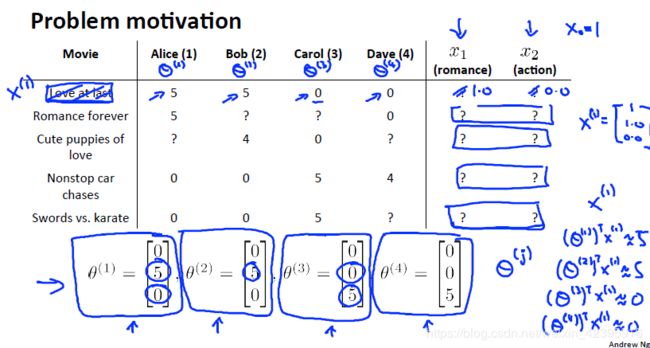
根据第一部分的分析，很容易得到由${\theta }^{(1)},{\theta }^{(2)},....,{\theta }^{(n_u)}$，求$x^{(1)},x^{(2)},...,x^{(n_m)}$的目标函数：
$$mi{n}_{x^{(1)},x^{(2)},...,x^{(n_m)}}\frac{1}{2}\sum _{i=1}^{n_m}\sum _{j:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i.j)}{)}^2+\frac{\lambda }{2}\sum _{i=1}^{n_m}\sum _{k=1}^n(x_k^{(i)}{)}^2$$

也就是说，我们知道$\theta$就能学习$x$，知道$x$也能学习$\theta$.
因此，我们可以先随机初始化一组$\theta$，学习出$x$，并根据已有的一些电影的原始特征，优化出更好的$\theta$。重复$\theta \to x\to \theta \to x\to \theta \to x$的过程，最终算法将会收敛到合理的$\theta$和$x$。这一过程，我们称之为协同过滤(collaborative filtering)。
\quad

2.2 Collaborative filtering algorithm

同时最小化${\theta }^{(1)},{\theta }^{(2)},....,{\theta }^{(n_u)}$和$x^{(1)},x^{(2)},...,x^{(n_m)}$：
$$J=\frac{1}{2}\sum _{(i,j):r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i.j)}{)}^2+\frac{\lambda }{2}\sum _{i=1}^{n_m}\sum _{k=1}^n(x_k^{(i)}{)}^2+\frac{\lambda }{2}\sum _{j=1}^{n_u}\sum _{k=1}^n({\theta }_k^{(j)}{)}^2$$
$$mi{n}_{{\theta }^{(1)},....,{\theta }^{(n_u)},x^{(1)},...,x^{(n_m)}}J({\theta }^{(1)},....,{\theta }^{(n_u)},x^{(1)},...,x^{(n_m)})$$