计算机视觉——计算视图差(python)
计算视差图
- 一、原理
- 1.立体重建算法
- 2.立体匹配分类
- 3.立体匹配步骤
- 二、实现NCC
- 1.NCC算法代码
- 2.增加高斯滤波器
- 3.调用
- 三、分析实验
- 1.实验结果
- 2.对比实验
- 四、总结
- 遇到的问题
一、原理
1.立体重建算法
立体重建:基于视觉的三维重建,指的是通过摄像机获取场景物体的数据图像,并对此图像进行分析处理,再结合计算机视觉知识推导出现实环境中物体的三维信息。
在本文介绍的该种算法中,我们将对于每个像素尝试不同的偏移,并按照局部图像周围 归一化的互相关值,选择具有最好分数的偏移,然后记录下该最佳偏移。因为每个 偏移在某种程度上对应于一个平面,所以该过程有时称为扫平面法。
注:虽然该方法并不是立体重建中最好的方法,但是非常简单,通常会得出令人满意的结果。
2.立体匹配分类
在立体匹配中,匹配问题可以看成是寻找两组数据相关程度的过程。立体匹配算法有多种分类。
①根据算法运行时约束的作用范围:分为局部(local)匹配算法和全局(Global)匹配算法。
全局匹配算法一般定义如下能量函数:
E ( d ) = E d a t a ( d ) + E s m o o t h ( d ) = ∑ p ∈ R C ( p , d ) + ∑ q , p ∈ R P ( d q − d p ) E(d)=E_{data}(d)+E_{smooth}(d)=\sum_{p\in R}C(p,d)+\sum_{q,p\in R}P(d_{q}-d_{p}) E(d)=Edata(d)+Esmooth(d)=p∈R∑C(p,d)+q,p∈R∑P(dq−dp)
其中 E d a t a ( d ) E_{data}(d) Edata(d)描述了匹配程度, E s m o o t h ( d ) E_{smooth}(d) Esmooth(d)是定义场景的约束,C是匹配代价,P是不同两个像素p和q视差的函数,一般称作惩罚项。
即使全局算法具有准确性较高的优点,其计算速度确非常慢,在实时性要求高的场合不适合使用全局立体匹配算法。
②基于生成的视差图:可分为稠密(Dense)匹配和稀疏(Sparse)匹配。
3.立体匹配步骤
深度恢复:
通过上述匹配结果得到的视差图D,我们可以很简单的利用相似三角形反推出以左视图为参考系的深度图。
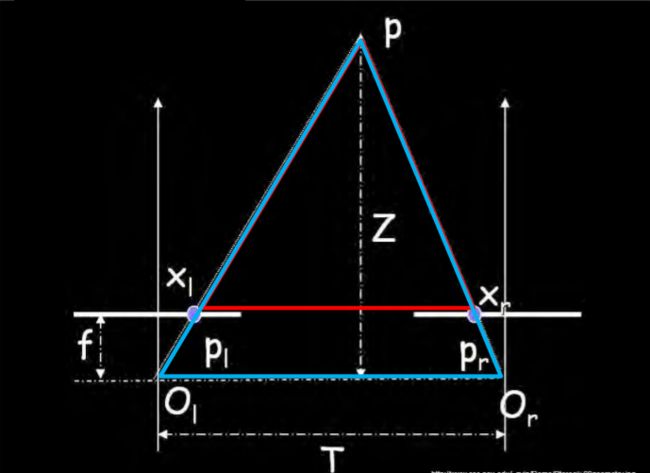
T为双目相机基线,f为相机焦距,这些可以通过相机标定得到,xr-xl就是视差d。通过 z = f ∗ T / d z=f*T/d z=f∗T/d.
- 匹配代价计算
目的是衡量待匹配像素与候选像素之间的相关性。两个像素无论是否为同名点,都可以通过匹配代价函数计算匹配代价,代价越小则说明相关性越大,是同名点的概率也越大。
每个像素在搜索同名点之前,往往会指定一个视差搜索范围D(Dmin ~ Dmax),视差搜索时将范围限定在D内,用一个大小为W×H×D(W为影像宽度,H为影像高度)的三维矩阵C来存储每个像素在视差范围内每个视差下的匹配代价值。矩阵C通常称为DSI(Disparity Space Image)。
匹配代价计算的方法有很多,使用灰度绝对值差(AD,Absolute Differences)、灰度绝对值差之和(SAD,Sum of Absolute Differences)、归一化相关系数(NCC,Normalized Cross-correlation)等方法来计算两个像素的匹配代价。 - 代价聚合
全局算法基于原始匹配代价进行后续算法计算。而区域算法则需要通过窗口叠加来增强匹配代价的可靠性,根据原始匹配代价不同,可分为:
C(x, y, d)为像素点 (x, y)在视差为d情况 下的匹配误差.
绝对差值和SAD:
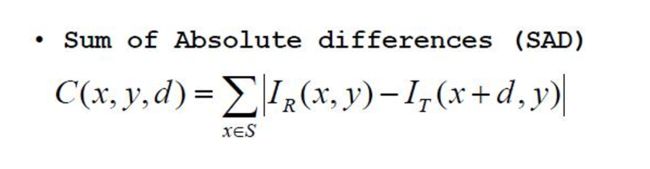
截断绝对差值和STAD:
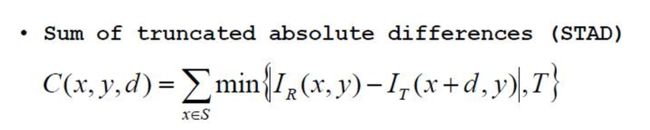
差值平方和SSD:
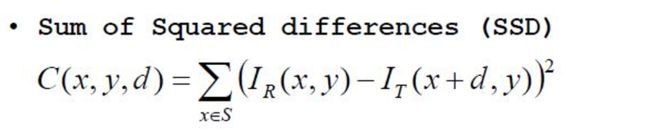
- 视差计算
视差计算即通过代价聚合之后的代价矩阵S来确定每个像素的最优视差值,通常使用赢家通吃算法(WTA,Winner-Takes-All)来计算,即某个像素的所有视差下的代价值中,选择最小代价值所对应的视差作为最优视差。.而全局算法则直接对原始匹配代价进行处理,一般会先给出一个能量评价函数,然后通过不同的优化算法来求得能量的最小值,同时每个点的视差值也就计算出来了。 - 视差优化
视差优化的目的是对上一步得到的视差图进行进一步优化,改善视差图的质量,包括剔除错误视差、适当平滑以及子像素精度优化等步骤,一般采用左右一致性检查(Left-Right Check)算法剔除因为遮挡和噪声而导致的错误视差;采用剔除小连通区域算法来剔除孤立异常点。
采用中值滤波(Median Filter)、双边滤波(Bilateral Filter)等平滑算法对视差图进行平滑;另外还有一些有效提高视差图质量的方法如鲁棒平面拟合(Robust Plane Fitting)、亮度一致性约束(Intensity Consistent)、局部一致性约束(Locally Consistent)等也常被使用。
本实验中是使用 高斯滤波器替换均匀滤波器,产生更加平滑视差图的例子。
二、实现NCC
1.NCC算法代码
# -*- coding:utf-8 _*-
import math
import numpy as np
from numpy import roll
from numpy import *
from numpy import argmax
from math import sqrt
from scipy.ndimage import filters
def plane_sweep_ncc(im_l,im_r,start,steps,wid):
""" 使用归一化的互相关计算视差图像 """
m,n = im_l.shape
# 保存不同求和值的数组
mean_l = zeros((m,n))
mean_r = zeros((m,n))
s = zeros((m,n))
s_l = zeros((m,n))
s_r = zeros((m,n))
# 保存深度平面的数组
dmaps = zeros((m,n,steps))
# 计算图像块的平均值
filters.uniform_filter(im_l,wid,mean_l)
filters.uniform_filter(im_r,wid,mean_r)
# 归一化图像
norm_l = im_l - mean_l
norm_r = im_r - mean_r
# 尝试不同的视差
for displ in range(steps):
# 将左边图像移动到右边,计算加和
filters.uniform_filter(roll(norm_l,-displ-start)*norm_r,wid,s) # 和归一化
filters.uniform_filter(roll(norm_l,-displ-start)*roll(norm_l,-displ-start),wid,s_l)
filters.uniform_filter(norm_r*norm_r,wid,s_r) # 和反归一化
# 保存 ncc 的分数
dmaps[:,:,displ] = s/np.sqrt(s_l*s_r)
# 为每个像素选取最佳深度
return argmax(dmaps,axis=2)
2.增加高斯滤波器
def plane_sweep_gauss(im_l,im_r,start,steps,wid):
#使用带有高斯加权周边的归一化互相关计算视差图像 """
m,n = im_l.shape
# 保存不同加和的数组
mean_l = zeros((m,n))
mean_r = zeros((m,n))
s = zeros((m,n))
s_l = zeros((m,n))
s_r = zeros((m,n))
# 保存深度平面的数组
dmaps = zeros((m,n,steps))
# 计算平均值
filters.gaussian_filter(im_l,wid,0,mean_l)
filters.gaussian_filter(im_r,wid,0,mean_r)
# 归一化图像
norm_l = im_l - mean_l
norm_r = im_r - mean_r
# 尝试不同的视差
for displ in range(steps):
# 将左边图像移动到右边,计算加和
filters.gaussian_filter(roll(norm_l,-displ-start)*norm_r,wid,0,s) # 和归一化
filters.gaussian_filter(roll(norm_l,-displ-start)*roll(norm_l,-displ-start),wid,0,s_l)
filters.gaussian_filter(norm_r*norm_r,wid,0,s_r) # 和反归一化
# 保存 ncc 的分数
dmaps[:,:,displ] = s/sqrt(s_l*s_r)
# 为每个像素选取最佳深度
return argmax(dmaps,axis=2)
3.调用
# -*- coding:utf-8 _*-
import stereo
import array
from PIL import Image
from pylab import *
import imageio
im_l = array(Image.open(r'D:\CVphoto\cones-ppm-2\cones\im2.ppm').convert('L'),'f')
im_r = array(Image.open(r'D:\CVphoto\cones-ppm-2\cones\im6.ppm').convert('L'),'f')
#im_l = array(Image.open(r'D:\CVphoto\cones-ppm-2\cones\im2.ppm').convert('L'))
#im_r = array(Image.open(r'D:\CVphoto\cones-ppm-2\cones\im6.ppm').convert('L'))
# 开始偏移,并设置步长
steps = 12
start = 4
# ncc 的宽度
wid = 9
res = stereo.plane_sweep_ncc(im_l,im_r,start,steps,wid)
import scipy.misc
scipy.misc.imsave('depth.png',res)
#scipy.misc.imageio.imwrite('depth.png',res)
三、分析实验
1.实验结果
原条件下 :im2.ppm(左)和im6.ppm(右)
原条件下 :steps=12,start=4,wid=9,分别实现ncc(左)和gauss(右)2.对比实验
- 修改wid值为3,分别实现ncc(左)和gauss(右)
- 修改wid值为9,分别实现ncc(左)和gauss(右)
- 修改wid值为11,分别实现ncc(左)和gauss(右)
- 修改wid值为50,实现ncc。
小结:可以明显看出,不管是调用ncc或者加了高斯滤波器之后的gauss,当wid值越小,图像越密集,wid值越大图像轮廓更清晰一点,所以在窗口值很小时,会有更多的细节,噪声也会更大,当窗口值更大,有更强的鲁棒性,更加稳健,但与此同时也丢失了很多细节。
当有一个很大的wid时,边缘的细节将不再清晰,接近中心的位置的图像更加被突出。
所以我们要选择一个合适的窗口大小,使其在具有一定清晰度的情况下还可以有一定的稳定性。
同时可以看出与标准版本相比,高斯版本具有较少的噪声,但缺少很多细节信息。
在标准版本中设置 wid 为 9,高斯版本中设置 wid 为 3。
- 修改steps值为20,分别实现ncc(左)和gauss(右)
- 修改steps值为50,starts和wid分别为4,9,使用ncc实现。
小结:可以看出,在立体图像的边缘处和棱角处更容易出现模糊的重影,猜测应该是因为两幅视图的视差在这些地方相对大一点,所以在这些有明显跨幅的地方,模糊的更加厉害。
进行高斯滤波之后的图像边缘更加平滑。
四、总结
遇到的问题
-
报错:
TypeError: array() argument 1 or typecode must be char (string or ascii-unicode with length 1), not Image
错误原因:array()的第一参数必须是一个unicode,python array的第一个参数必须为一个typecode,用于表明支持初始化的类型,python自带的array只支持一维数组。
解决方法:使用import array。 -
报错:
TypeError: 'module' object is not callable
分析:Python导入模块的方法有两种,import module 和 from module import,报改错误应该是缺少模块
增加模块:from pylab import *和from numpy import * -
报错:
AttributeError: 'module' object has no attribute 'uniform_filter'
解决方法:增加from scipy.ndimage import filters -
报错:
TypeError: only size-1 arrays can be converted to Python scalars
分析:import math中的sqrt不能直接使用。
解决方法:dmaps[:,:,displ] = s/sqrt(s_l*s_r)中的sqrt不能之间使用,改成np.sqrt。(import numpy as np)











