【文献阅读】Asymmetric Non-local Neural Networks for Semantic Segmentation

原文链接：https://arxiv.org/abs/1908.07678
代码：https://github.com/MendelXu/ANN.git

---

Non-local 是一种特别有用的语义分割技术，但也因其难以进行计算和占用GPU内存而受到批评。本文提出了Asymmetric Non-local Neural Network，其中有两个突出的组成部分：Asymmetric Pyramid Non-local Block（APNB） 和 Asymmetric Fusion Non-local Block（AFNB）。APNB利用金字塔采样模块，在不牺牲性能的前提下，极大地减少了计算和内存消耗；AFNB是由APNB演化而来的，在充分考虑了长期相关性的前提下，融合了不同层次的特征，从而大大提高了性能。

核心思路是：
只要query分支和key分支的输出保持相同的大小，Non-local的输出大小就保持不变。考虑到这一点，如果只从key分支和value分支中选取几个有代表性的点作为样本，就有可能在不牺牲性能的情况下显著降低时间复杂度。如下图所示，其中，$S\ll N$。

---

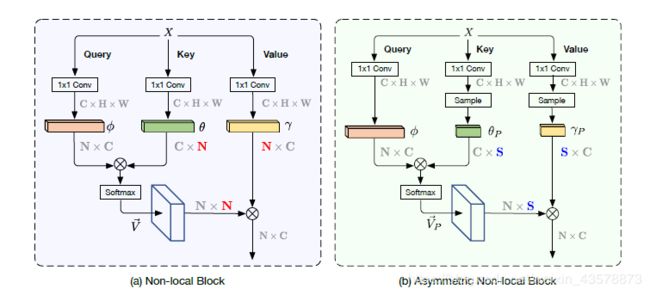
Asymmetric Non-local Neural Network

提出了APNB和AFNB，其中APNB旨在减少Non-local的计算开销，AFNB提高了Non-local的学习能力，从而提高了分割性能。

重识Non-local

考虑输入特征图$X\in {\mathbb{R}}^{C\times H\times W}$，三个$1\times 1$卷积$W_{\varphi }$、$W_{\theta }$和$W_{\gamma }$用来将$X$变换到不同的嵌入式空间$\varphi \in {\mathbb{R}}^{C^{\prime }\times H\times W}$、$\theta \in {\mathbb{R}}^{C^{\prime }\times H\times W}$、$\gamma \in {\mathbb{R}}^{C^{\prime }\times H\times W}$
$$\varphi =W_{\varphi }(X),\theta =W_{\theta }(X),\gamma =W_{\gamma }(X)$$
接着将他们三个$flatten$为$C^{\prime }\times N$，$N$为空间中总像素数，$N=H\times W$。相似度矩阵$V\in {\mathbb{R}}^{N\times N}$可由矩阵乘法计算
$$V={\varphi }^T\times \theta$$
接着，将$V$进行归一化
$$V=f(V)$$
$f$有三种形式，分别为$softmax$、$rescaling$和$none$，这里选择用$softmax$。对于$\gamma$中的每个位置，都可以计算输出为
$$O=V\times {\gamma }^T$$
其中，$O\in {\mathbb{R}}^{N\times C^{\prime }}$。通过参考Non-local的设计，最终的输出为
$$Y=W_o(O^T)+XorY=cat(W_o(O^T),X)$$
其中，$W_o$使用$1\times 1$卷积，作为一个加权参数来调整Non-local的重要性，并且将通道维度从$C^{\prime }$还原为$C$。

Asymmetric Pyramid Nonlocal Block（APNB）

动机和分析

Non-local在两个矩阵相乘的时间复杂度为$O(C^{\prime }{N}^2)=O(C^{\prime }{H}^2{W}^2)$。在语义分割任务中，网络的输出通常有较大的分辨率来保持细节的语义信息，$N$通常很大。
一个更直接的$pipeline$如下：
$${\mathbb{R}}^{N\times C^{\prime }}\times {\mathbb{R}}^{C^{\prime }\times N}\to {\mathbb{R}}^{N\times N}\times {\mathbb{R}}^{N\times C^{\prime }}\to {\mathbb{R}}^{N\times C^{\prime }}$$
通过将$N$变为$S$（$S\ll N$），输出尺寸保持不变
$${\mathbb{R}}^{N\times C^{\prime }}\times {\mathbb{R}}^{C^{\prime }\times S}\to {\mathbb{R}}^{N\times S}\times {\mathbb{R}}^{S\times C^{\prime }}\to {\mathbb{R}}^{N\times C^{\prime }}$$
将$N$变为更小的$S$相当于从图中采样几个有代表性的点，而不是考虑空间中所有的点，从而将计算量大大减少。

方法

在$\theta$和$\gamma$后，通过添加采样模块$P_{\theta }$和$P_{\gamma }$，来采样一些稀疏的锚点，得到${\theta }_P\in {\mathbb{R}}^{C^{\prime }\times S}$和${\gamma }_P\in {\mathbb{R}}^{C^{\prime }\times S}$，其中$S$为采样锚点的个数。数学公式为
$${\theta }_P=P_{\theta }(\theta ),{\gamma }_P=P_{\gamma }(\gamma )$$
$\varphi$与锚点${\theta }_P$间的相似度矩阵$V_P$如下
$$V_P={\varphi }^T\times {\theta }_P$$
其中，$V_P$是一个不对称的矩阵，大小为$N\times S$。接下来与Non-local一样进行归一化，得到$V_P$。$attention$输出为
$$O_P=V_P\times {\gamma }_P^T$$
最终的输出$Y_P$为
$$Y_P=cat(W_o(O_P^T),X)$$
时间复杂度仅为$O(C^{\prime }NS)$，比标准Non-local中的$O(C^{\prime }{N}^2)$小很多。

前面的工作表明，全局和多尺度对语义分割很有帮助，因此，在Non-local块中嵌入金字塔池化来增强全局表示。

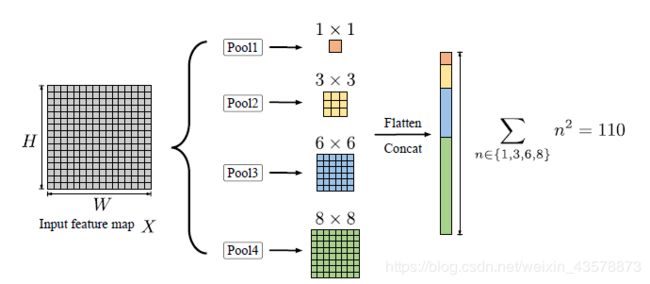
这四个池化结果被平铺并连接起来，作为被采样的点。设置$n\subseteq \{1,3,6,8\}$，则锚点的总量为
$$S=110=\sum _{n\subseteq \{1,3,6,8\}}{n}^2$$

Asymmetric Fusion Nonlocal Block（AFNB）

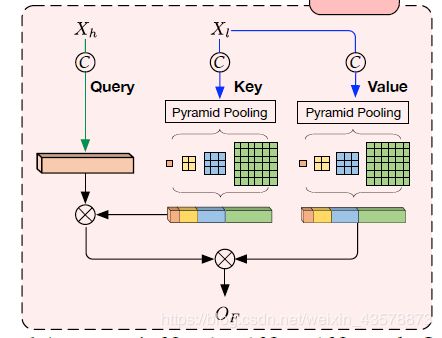
不同层级的特征融合对语义分割有帮助，将特征融合加入到Non-local中，得到Fusion Non-local Block。
标准的Non-local只有一个输入源，而FNB有两个输入源：一个高级特征图$X_h\in {\mathbb{R}}^{C_h\times N_h}$和一个低级特征图$X_l\in {\mathbb{R}}^{C_l\times N_l}$。同样的，$1\times 1$卷积$W_{\varphi }^h$、$W_{\theta }^l$和$W_{\gamma }^l$被用来将$X_h$和$X_l$变换到嵌入式空间${\varphi }_h\in {\mathbb{R}}^{C^{\prime }\times N_h}$、${\theta }_l\in {\mathbb{R}}^{C^{\prime }\times N_l}$和${\gamma }_l\in {\mathbb{R}}^{C^{\prime }\times N_l}$
$${\varphi }_h=W_{\varphi }^h(X_h),{\theta }_l=W_{\theta }^l(X_l),{\gamma }_l=W_{\gamma }^l(X_l)$$
${\varphi }_h$和${\theta }_l$间的相似度矩阵$V_F\in {\mathbb{R}}^{N_h\times N_l}$为
$$V_F={\varphi }_h^T\times {\theta }_l$$
同样的，将$V_F$进行归一化得到$V_F\in {\mathbb{R}}^{N_h\times N_l}$。同理输出为
$$O_F=V_F\times {\gamma }_l^T$$

$$Y_P=cat(W_o(O_P^T),X)$$

网络结构

---

实验结果