c语言函数调用及应用举例
一,函数的定义
一般来说,执行源程序就是执行主函数main,其他函数只能被主函数所调用,而其他函数之间也可以相互调用。
1.标准库函数:
分为:I/O函数,字符串,字符处理函数,数学函数,接口函数,时间转换和操作函数,动态地址分配函数,目录函数,过程控制函数,字符屏幕和图形功能函数。
这些库函数在不同的头文件中声明。比如:
math.h头文件中有:sin(x),cos(x),exp(x)(求e^x),fabs(x)(求x的绝对值)等库函数。
stdio.h头文件中有:scanf(),printf(),gets(),puts(),getchar(),putchar()等库函数。
string.h头文件中有:strcmp(),strcpy(),strcat(),strlen等库函数。
2.函数的定义:
(1)定义无参函数:
类型名 函数名()
{
函数体
}
or
类型名 函数名(void)
{
函数体
}
(2)定义有参函数
类型名 函数名(形式参数表列)
{
函数体
}
(3)定义空函数
类型名 函数名()
{ }
二,函数的调用
1.函数调用时的参数传递
函数间通过参数来传递数据,即通过主调函数中的实际参数(实参)向被调用函数中的形式参数(形参)进行传递。
实参向形参传递数据的方式:实参将值单向传递给形参,形参的变化不影响实参值。
for example:
#include
#include
int main()
{
int a, b;
void swap(int a, int b); //函数声明
scanf("%d%d", &a, &b); //键盘输入
swap(a, b); //函数调用
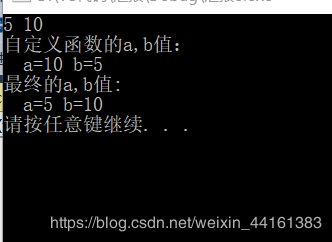
printf("最终的a,b值:\n a=%d b=%d\n", a, b);
system("pause");
return 0;
}
void swap(int a, int b)
{
int t;
if (a < b)
{
t = a;
a = b;
b = t; //a中放大值,b中放小值
}
printf("自定义函数的a,b值:\n a=%d b=%d\n", a, b);
}
运行结果为:
分析:形参交换了数据,而实参保持原数据不变。这是单向的值传递,所以形参的值改变后而实参的值没有改变。
- 形参在函数中是变量名,在函数调用时,形参被临时分配相应的内存,调用结束后,形参单元被释放,而实参单元保留并维持原值。
- 实参是表达式,负责向对应的形参标识的内存单元传递数据,实参向形参的数据传递是“值传递”。
- 实参与形参必须个数相同
- 对应的形参和实参的类型必须一致
2.函数的返回值
(1)函数的返回值通过函数中的return语句获得。如果需要从调用函数带回一个函数值(供主函数使用),被调函数中需包含return语句。
for example:
int max(int x,int y)
{
return(x>y?x:y);
}(2)在定义函数时要指定函数值的类型
int max(float x,float y) //函数值为整型
char letter(char c1,char c2) //函数值为字符型
double max(int x,int y) //函数值为双精度型(3)函数类型决定返回值的类型。
3.函数的嵌套
定义函数时不能定义另一个函数,但是可以进行嵌套调用函数。
for example:
*用函数嵌套找出4个数中的最大值。
#include
#include
int max2(int a, int b) //找出a和b中的最大值
{
if (a >= b)
{
return a; // a作为返回值
}
return b; // b作为返回值
}
int max4(int a, int b, int c, int d) //定义找4个数最大值的函数
{
int m; //存最大值
m = max2(a, b); //调用max2函数,将a,b中大的值放在m中
m = max2(m, c); //调用max2函数,将a,b,c中大的值放在m中
m = max2(m, d); //调用max2函数,将a,b,c,d中大的值放在m中
return m; //返回到主函数
}
int main()
{
int a, b, c, d;
int max;
printf("请输入四个数:\n");
scanf("%d%d%d%d", &a, &b, &c, &d);
max = max4(a, b, c, d); //调用max4函数
printf("最大数位:%d\n", max);
system("pause");
return 0;
}
三,函数的递归
1.递归概念:
函数的递归调用是指:一个函数在他的函数体内直接或间接地调用它自身。分为:直接递归(函数直接调用自身)和间接递归(函数通过其他函数调用自身)。可分为“回溯”和“递推”两个阶段。
2.递归函数的一般形式:
反值类型 递归函数名(参数说明表)
{
if(递归终止条件)
返回值=递归终止值;
else
返回值=递归调用(...)的表达式;
return 返回值;
}
3.递归函数举例:
*用递归求n的阶乘。
#include
#include
int fac(int n) //定义函数
{
int f;
if (n < 0)
printf("数据错误\n");
else if (n == 0 || n == 1)
f = 1;
else
f = n* fac(n - 1); //n!=n*(n-1)
return f; //返回主函数
}
int main()
{
int n, y;
printf("请输入n的值\n");
scanf("%d", &n);
y = fac(n); //这里n为实参
printf("%d!=%d\n", n, y);
system("pause");
return 0;
} 汉诺塔问题为经典的递归调用实例。代码如下:
#include
#include
void move(char x, char y) //输出移盘方案
{
printf("%c->%c\n", x, y);
}
void hanoi(int n, char one, char two, char three) //移盘
{
if (n == 1)
move(one, three); //如果是1个盘,直接从第一个座移到第3个座上
else
{
hanoi(n - 1, one, three, two);
move(one, three);
hanoi(n - 1, two, one, three);
}
}
int main()
{
int n;
printf("输入盘的个数\n");
scanf("%d", &n);
printf("移盘的步骤:\n");
hanoi(n, 'A', 'B', 'C');
system("pause");
return 0;
分析:将n个盘子从A座上移到C座上需要三步:
(1)将A上的n-1个盘子借助C座先移到B座上;
(2)把A座上剩下的一个盘子移到C座上;
(3)将n-1个盘从B座上借助于A移到C座上。