关于组合数的一些东西

组合数对应着杨辉三角杨辉三角中第i行j个表示 Cj−1i−1

由组合数的定义

Cji=Ci−ji

根据二项式展开 (x+1)n=∑ni=0Cinxi

x=1时∑ni=0Cin=2n

∑2|i,i≤nCin=∑2/|n,i≤nCin=2

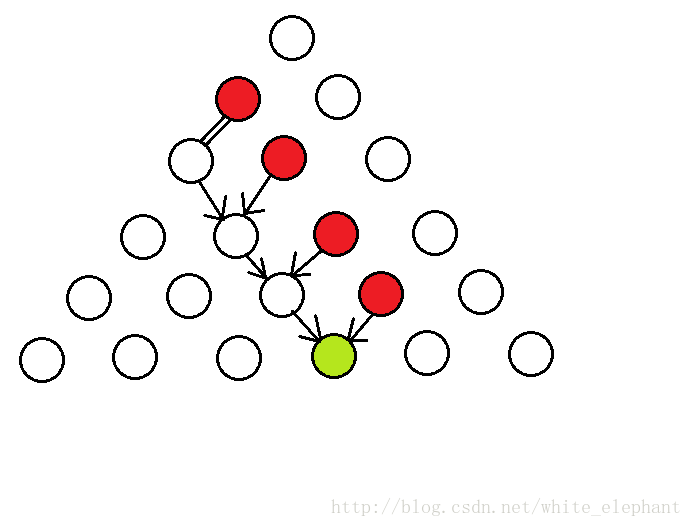
这个可以在杨辉三角上将每一个点分解得出：
当 2|n ，由于有对称性，证明显然
当 2/|n ，如图

∑di=0Cin+i=Cdn+d+1

同样，将杨辉三角上的点合并：

Caa+b+c∗Cbb+c=Caa+b∗Cca+b+c

证明：左式=(a+b+c)!a!(b+c)!∗(b+c)!b!c!=(a+b+c)!a!b!c!=(a+b)!a!b!∗(a+b+c)!(a+b)!c!=Cca+b+c∗Caa+b

也可以用定义证明。

然后是一道题

【51nod 1362】推箱子

大意：

n*m的网格图从格点(0,0)走到第n行的某个格子停止，要求只能向下或向右，或到右下方的格子
即(x,y)走到(x+1,y),(x,y+1),(x+1,y+1)

问方案数，对X取模
1≤n≤800,1≤m,X≤2∗109
多组数据

Input

1 2 10
3 3 100

Output

9
96

---

n这么小？！

枚举终点
再枚举斜着走i格，然后套上组合数：

Ans=∑p=0m∑i=0min(p,n)Cin+p−i∗Cn−in−i+p−i  发现(n−i)+(p−i)+i=n+p−i=∑p=0m∑i=0min(p,n)Cin∗Cp−in+p−i=∑i=0min(n,m)Cin∑p=imCnn+p−i=∑i=0min(n,m)Cin∑p′=0m−iCnn+p′ p′代替p−i，发现可以套另一个公式=∑i=0min(n,m)Cni∗Cn+1n+m−i+1

%X怎么办？

X不是质数！！

X不是质数就不能用费马小定理求逆元。

欧拉定理求逆元呢？
那要互质啊。

诶n<=800！

那我们直接强行分解质因数就好了！！
然而质因数个数？

想到由于x的质因数很小，所以，与x互质的分母直接用欧拉定理求逆元。其他的强算即可。

记得要用快速乘，不然unsignedll都会爆。

code:

#include
#include
#define ll long long

using namespace std;

int pr[100100],s[100100],d[100100],n,m,t,ola,c[1000][1000];
ll x,ans,Ans,div;
bool bz[100100];

void swap(int &a,int &b){a^=b,b^=a,a^=b;}

ll qmul(ll a,ll b){
    b%=x;a%=x;
    ll r=0;for(;b;b>>=1,a=(a+a)%x)if(b&1)r=(r+a)%x;return r;
}
ll qpow(ll a,int b){
    a%=x;
    ll r=1;for(;b;b>>=1,a=qmul(a,a))if(b&1)r=qmul(r,a);return r;
}

void inc(int x){
    for(int n,i=1;i<=t;i++)if(x%d[i]==0){
        n=0;do n++,x/=d[i];while(x%d[i]==0);
        s[i]+=n;
    }ans=qmul(ans,(ll)x);
}
void dec(int x){
    for(int n,i=1;i<=t;i++)if(x%d[i]==0){
        n=0;do n++,x/=d[i];while(x%d[i]==0);
        s[i]-=n;
    }div=qmul(div,(ll)x);
}

int main(){
    for(int i=2;i<100000;i++){
        if(!bz[i])pr[++pr[0]]=i;
        for(int j=1;j<=pr[0] && i*pr[j]<100000;j++){
            bz[i*pr[j]]=1;if(i%pr[j]==0)break;
        }
    }
    while(~scanf("%d %d %lld",&n,&m,&x)){
        t=0;Ans=0;ola=1;
        for(int i=1,tmp=x;i<=pr[0] && tmp!=1;i++){
            if(tmp%pr[i]==0){
                d[++t]=pr[i];tmp/=pr[i];ola=ola*(pr[i]-1);
                while(tmp%pr[i]==0)tmp/=pr[i],ola=ola*pr[i];
            }
            if(tmp==1)break;
            if(pr[i]*pr[i]>tmp){d[++t]=tmp;ola=ola*(tmp-1);break;}
        }
        for(int i=0;i<=n && i<=m;i++){
            ans=1;div=1;
            for(int j=1;j<=t;j++)s[j]=0;
            for(int j=0;j1);
            for(int j=0;j<=n;j++)inc(n+m-i+1-j),dec(j+1);
            for(int j=1;j<=t;j++)ans=qmul(ans,qpow((ll)d[j],s[j]));
            Ans=(Ans+qmul(ans,qpow(div,ola-1)))%x;
        }printf("%lld\n",Ans);
    }
}