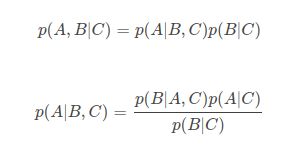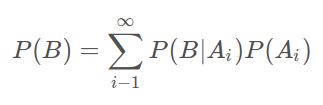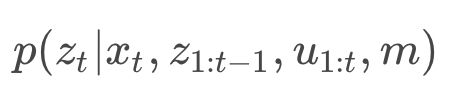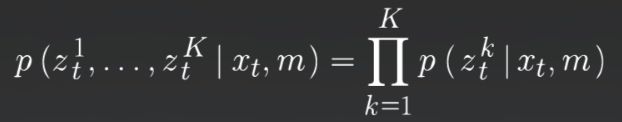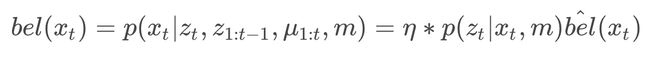自动驾驶定位技术-马尔科夫定位
Localization
Github: https://github.com/williamhyin/CarND-Kidnapped-Vehicle
Email: [email protected]
知乎专栏: 自动驾驶全栈工程师
Definition of Localization
-
汽车会收集当前环境的信息,并和已知地图对比,推断它在世界上的位置. 简而言之, 自动驾驶定位技术就是解决“我在哪儿”的问题, 并且对可靠性和安全性提出了非常高的要求.
-
自动驾驶中定位的要求: 精确度达到10 cm及以下, 车载传感器可用于估计本地测量值和给定地图之间的转换.
-
已有的定位解决方案:
- GPS 定位: 精度太低: 1-3 m; 更新速度慢: 10次/s; 容易受到遮挡物的影响, 检测到的卫星数量很少.
- 惯性传感器: 利用加速度计和陀螺仪, 根据上一时刻的位置和方位推断现在的位置和方位, 即航迹推测. 惯性导航和GPS可以结合起来使用, 惯性导航可以弥补GPS更新频率低的缺陷, GPS可以纠正惯性导航的运动误差. 但是, 如果是在地下隧道或者其他信号不好的地方, GPS可能无法及时纠正惯性导航的运动误差.
- 传感器融合: 利用RADAR 和LIDAR, 记录道路外观的图像, 测量车辆到静态物体如建筑物,电线杆,路缘的距离, 将传感器的点云数据与高精地图储存的特征进行匹配, 并实现车辆坐标系与世界坐标系之间的转换, 确定最有可能位于的位置.
- 摄像头: 利用摄像头, 记录道路外观的图像, 将摄像头的数据与地图进行匹配, 确定最有可能位于的位置
-
自动驾驶定位技术的组合方案:
- 基于 GPS 和惯性传感器的传感器融合
- 基于 LiDAR 点云与高精地图的匹配 (研究方向: 粒子滤波, 深度学习)
- 基于视觉的道路特征识别
-
应用实例:
首先根据GPS的数据(经纬高和航向)确定无人车大致处于哪条道路上, 这个位置的可能与真实位置有5~10米的差距. 然后根据车载传感器检测的车道线(虚、实线)及道路边缘(路沿或护栏)的距离与高精地图提供的车道线及道路边缘做比对, 然后修正无人车的横向定位. 根据车载传感器检测到的广告牌、红绿灯、墙上的标志、地上的标志(停止线、箭头等), 与高精地图提供的同一道路特征(POI)进行匹配, 进而修正纵向定位和航向. 在没有检测到任何道路特征的情况下, 可以通过航位推算进行短时间的位置推算. 无人车的定位算法通常采用粒子滤波的方法, 需要多个计算周期后, 定位结果才会收敛, 进而提供一个相对稳定的定位结果.
基于视觉的道路特征识别, 由于容易受到天气的影响, 因此目前主要作为定位补充手段. 而且通常是将Lidar和视觉系统结合进行定位. 这种方法需要预先准备一幅激光雷达制造的3D地图, 用Ground-Plane Sufficient得到一个2D的纯地面模型地图, 用OpenGL将单目视觉图像与这个2D的纯地面模型地图经过坐标变换, 用归一化互信息配准. 然后用扩展卡尔曼滤波器(EKF)来实现定位.
Basic realization of Localization
马尔可夫定位或贝叶斯滤波是通常的定位滤波器. 我们通常认为我们的车辆位置作为一个概率分布,每次我们移动,我们的分布变得更分散(更广泛). 我们将变量(地图数据、观测数据和控制数据)传递到过滤器中,以便在每个时间步骤中集中(缩小)这种分布. 应用过滤器之前的每个状态代表我们的先验,而变窄的分布代表我们的贝叶斯后验.
1. 贝叶斯法则(Bayes Rule)
贝叶斯规则是马尔可夫局部化的基础.
我们可以将贝叶斯规则应用到车辆定位中, 通过在每个时间步骤中传递贝叶斯规则的变量来实现车辆的定位. 这就是所谓的本地化贝叶斯过滤器. 你可能认识到这类似于卡尔曼滤波器. 事实上, 许多定位滤波器,包括卡尔曼滤波器都是贝叶斯滤波器的特例.
P(location|observation): This is P(a|b), the normalized probability of a position given an observation (posterior).
P(observation|location): This is P(b|a), the probability of an observation given a position (likelihood)
P(location): This is P(a), the prior probability of a position (initialized by GPS + IMU)
P(observation): This is P(b), the total probability of an observation (Radar or Lidar)
两个重要的贝叶斯公式:
2. 后验概率(Localization Posterior)
-
假设我们出门堵车的可能因素有两个: 车辆太多和交通事故.
那么如果我们出门之前我们听到新闻说今天路上出了个交通事故,那么我们想算一下堵车的概率, 这个就叫做条件概率 .也就是P(堵车|交通事故).这是有因求果.
如果我们已经出了门, 然后遇到了堵车, 那么我们想算一下堵车时由交通事故引起的概率有多大,
那这个就叫做后验概率 (也是条件概率,但是通常习惯这么说).也就是P(交通事故|堵车).这是有果求因.
-
我们的目标是估计状态信度 bel (xt) ,不需要使用我们的整个观察历史. 我们将通过操作后验 *p(xt∣z1:t−1,μ1:t,m)得到一个递归状态估计量来实现这一点. 为此,我们必须证明我们当前的信度bel (xt)*可以用早一步的信度 *bel (xt-1)*来表示, 然后使用新的数据只更新当前的信度. 这种递归过滤器称为贝叶斯定位过滤器或马尔可夫定位过滤器, 使我们能够避免携带历史观测和运动数据. 我们将使用贝叶斯规则, 全概率公式和马尔可夫假设来实现这种递归状态估计器.
z_{1:t} represents the observation vector from time 0 to t (range measurements, bearing, images,etc.).
u_{1:t} represents the control vector from time 0 to t (yaw/pitch/roll rates and velocities).
m represents the map (grid maps, feature maps, landmarks)
xt represents the pose (position (x,y) + orientation \θ)
-
通过将观测向量 z1:t 分解为当前观测值 zt 和先前信息 z1:t−1, 我们向递归结构迈出了第一步.
现在, 我们应用贝叶斯规则:
值得注意的是, 当前观察都不包括在运动模型中. 我们将正规化因子定义为n, 1/n 为所有可能状态xt(i)上的观察和运动模型信度的总和. 也就是说我们只需要定义观察和运动模型来估算信度.
3. 运动模型(Motion Model)
运动模型是一个先验条件, 我们可以使用全概率公式对运动模型进行分解:

我们可以利用马尔可夫假设简化运动模型.
马尔可夫假设是指未来状态的条件概率分布只依赖于当前状态, 而不依赖于前面的其他状态. 这在数学上可以表 示为:
P(xt∣x_t-1,….,xt−i,….,x0)=P(xt∣xt−1)
需要注意的是, 当前状态可能包含前面状态的所有信息.
在这种情况下, 我们可以为运动模型提出两个假设:
-
由于我们(假设地)知道系统在时间步骤 t-1时的状态, 过去的观测值 z1: t-1和控制项 u1: t-1不能提供额外的信息来估计 xt 的后验值, 因为它们已经被用来估计 xt-1.
这意味着我们可以将 p(xt∣xt−1,z1:t−1,u1:t,m)** 简化为 p(xt∣xt−1,ut,m)**.
-
由于 ut是参考 xt-1的“在未来” , ut 没有告诉我们关于 xt-1的很多信息.
这意味着p(xt−1∣z1:t−1,u1:t,m)** 可以简化为 p(xt−1∣z1:t−1,u1:t−1,m).**

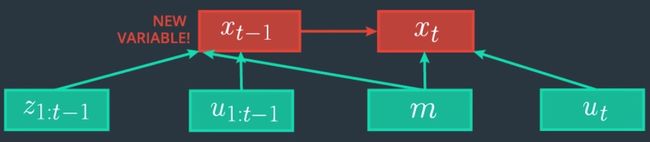
马尔可夫假设前的图形表示
马尔可夫假设后的图形表示
-
递归公式
令人惊奇的是, 我们有一个递归更新公式, 现在可以使用前一个时间步的估计状态来预测当前状态. 这是递归贝叶斯过滤器的关键步骤, 因为它使我们独立于整个观察和控制历史. 最后, 我们用整个 xi 上的和来代替积分, 因为在这种情况下我们有一个离散的局部化场景.
我们可以关注最后一步的求和是怎么做的. 它会查看车辆可能去过的每个地点 xt-1. 然后求和迭代每个可能的先验位置 xt-1(1) … xt-1(n). 对于列表中的每个可能的先前位置 xt-1(i) , 求和得出车辆确实在先前位置开始并最终在 xt 处结束的总概率.
对于每个可能的起始位置 xt-1, 我们如何计算这辆车真正从之前的位置开始并最终停在 xt 上的个体概率?
px(t) = p(xt∣xt−1) ∗ p(xt−1)
-
最终运动模型公式:
-
代码:
#include#include #include "helpers.h" using std::vector; vector initialize_priors(int map_size, vector landmark_positions, float position_stdev); float motion_model(float pseudo_position, float movement, vector priors, int map_size, int control_stdev); int main() { // set standard deviation of control: float control_stdev = 1.0f; // set standard deviation of position: float position_stdev = 1.0f; // meters vehicle moves per time step float movement_per_timestep = 1.0f; // number of x positions on map int map_size = 25; // initialize landmarks vector landmark_positions {5, 10, 20}; // initialize priors vector priors = initialize_priors(map_size, landmark_positions, position_stdev); // step through each pseudo position x (i) for (float i = 0; i < map_size; ++i) { float pseudo_position = i; // get the motion model probability for each x position float motion_prob = motion_model(pseudo_position, movement_per_timestep, priors, map_size, control_stdev); // print to stdout std::cout << pseudo_position << "\t" << motion_prob << std::endl; } return 0; } // TODO: implement the motion model: calculates prob of being at // an estimated position at time t float motion_model(float pseudo_position, float movement, vector priors, int map_size, int control_stdev) { // initialize probability float position_prob = 0.0f; // YOUR CODE HERE // loop over state space for all possible positions x (convolution): for (float j=0; j< map_size; ++j) { float next_pseudo_position = j; // distance from i to j float distance_ij = pseudo_position-next_pseudo_position; // transition probabilities: float transition_prob = Helpers::normpdf(distance_ij, movement, control_stdev); // estimate probability for the motion model, this is our prior position_prob += transition_prob*priors[j]; } return position_prob; } // initialize priors assuming vehicle at landmark +/- 1.0 meters position stdev vector initialize_priors(int map_size, vector landmark_positions, float position_stdev) { // set all priors to 0.0 vector priors(map_size, 0.0); // set each landmark positon +/-1 to 1.0/9.0 (9 possible postions) float norm_term = landmark_positions.size() * (position_stdev * 2 + 1); for (int i=0; i < landmark_positions.size(); ++i) { for (float j=1; j <= position_stdev; ++j) { priors.at(int(j+landmark_positions[i]+map_size)%map_size) += 1.0/norm_term; priors.at(int(-j+landmark_positions[i]+map_size)%map_size) += 1.0/norm_term; } priors.at(landmark_positions[i]) += 1.0/norm_term; } return priors; }
4. 观察模型(observation model)
马尔可夫假设可以帮助我们简化观测模型. 回想一下, 马尔可夫假设是下一个状态只依赖于前面的状态, 前面的状态信息已经被用于我们的状态估计. 因此, 我们可以忽略在 xt 之前的观察模型中的术语, 因为这些值已经在我们当前的状态中被考虑, 并且假设 t 是独立于以前的观察和控制的.
观察模型简化图
通过这些假设, 我们简化了我们的后验概率, 使得 t 处的观测值仅依赖于时间 t 的 x(位置) 和 m(地图).
由于 zt 可以是多个观测值的矢量, 我们改写了我们的观测模型来解释每个单一距离测量值的观测模型. 我们假设各个距离值 zt1到 ztk 的噪声行为是独立的, 并且我们的观测值是独立的, 这使得我们可以将观测模型表示为每个单个距离测量值的各个概率分布的乘积. 现在我们必须确定如何定义单一距离测量的观测模型.
由于传感器、传感器特定的噪声行为和性能以及地图类型的不同, 一般存在多种观测模型. 对于我们的一维例子, 我们假设我们的传感器测量驾驶方向上 n 个最接近的物体, 它们代表了我们地图上的地标. 我们还假设观测噪声可以被模拟为标准差为1米的高斯分布, 并且我们的传感器可以测量0-100米的范围.
为了实现观测模型, 我们使用给定的状态文本和给定的地图来估计伪距离, 假设你的车将站在地图上的特定位置 xt, 这些伪距离代表真正的距离值. 例如, 如果我们的车停在20号位置, 它会利用 xt 和 m 进行伪距(zt *)观测, 顺序是从第一个地标到最后一个地标的距离, 或者是5、11、39和57米. 与我们的实际观测(zt [19,37])相比, 20的位置似乎不太可能, 我们的观测更适合40左右的位置.
观测模型使用伪距估计和观测量作为输入.
观察模式将通过在每个时间步骤中执行以下步骤来实施:
-
测量行车方向(前进方向)距离车辆100米以内的地标距离
-
通过从地标位置减去伪位置来估计每个地标的伪位置
-
匹配每个伪距估计与其最接近的观测值
-
对于每个伪距和观测测量对, 通过将相关值传递给norm_pdf 来计算概率 :
norm_pdf(observation_measurement, pseudo_range_estimate, observation_stdev) -
返回所有概率的乘积
代码:
#include
#include
#include
#include "helpers.h"
using std::vector;
// function to get pseudo ranges
vector pseudo_range_estimator(vector landmark_positions,
float pseudo_position);
// observation model: calculate likelihood prob term based on landmark proximity
float observation_model(vector landmark_positions,
vector observations, vector pseudo_ranges,
float distance_max, float observation_stdev);
int main() {
// set observation standard deviation:
float observation_stdev = 1.0f;
// number of x positions on map
int map_size = 25;
// set distance max
float distance_max = map_size;
// define landmarks
vector landmark_positions {5, 10, 12, 20};
// define observations
vector observations {5.5, 13, 15};
// step through each pseudo position x (i)
for (int i = 0; i < map_size; ++i) {
float pseudo_position = float(i);
// get pseudo ranges
vector pseudo_ranges = pseudo_range_estimator(landmark_positions,
pseudo_position);
//get observation probability
float observation_prob = observation_model(landmark_positions, observations,
pseudo_ranges, distance_max,
observation_stdev);
//print to stdout
std::cout << observation_prob << std::endl;
}
return 0;
}
// TODO: Complete the observation model function
// calculates likelihood prob term based on landmark proximity
float observation_model(vector landmark_positions,
vector observations, vector pseudo_ranges,
float distance_max, float observation_stdev) {
float distance_prob=1.0f;
// YOUR CODE HERE
for (int z=0;z 0) {
// set min distance
pseudo_range_min = pseudo_ranges[0];
// remove this entry from pseudo_ranges-vector
pseudo_ranges.erase(pseudo_ranges.begin());
} else { // no or negative distances: set min distance to a large number
pseudo_range_min = std::numeric_limits::infinity();
}
// estimate the probability for observation model, this is our likelihood
distance_prob *= Helpers::normpdf(observations[z], pseudo_range_min,
observation_stdev);
}
return distance_prob;
}
vector pseudo_range_estimator(vector landmark_positions,
float pseudo_position) {
// define pseudo observation vector
vector pseudo_ranges;
// loop over number of landmarks and estimate pseudo ranges
for (int l=0; l< landmark_positions.size(); ++l) {
// estimate pseudo range for each single landmark
// and the current state position pose_i:
float range_l = landmark_positions[l] - pseudo_position;
// check if distances are positive:
if (range_l > 0.0f) {
pseudo_ranges.push_back(range_l);
}
}
// sort pseudo range vector
sort(pseudo_ranges.begin(), pseudo_ranges.end());
return pseudo_ranges;
}
5. 贝叶斯滤波/马尔科夫滤波完全公式( Full formula of Bayes Filter for localization)
这可以简化为:
这一概念可以用图表表示如下:
实现贝叶斯本地化过滤器的步骤如下
- first initializing priors
- extract sensor observations
-
for each pseudo-position:
- get the motion model probability
- determine pseudo ranges
- get the observation model probability
- use the motion and observation model probabilities to calculate the posterior probability
-
normalize posteriors (see helpers.h for a normalization function)
-
update priors (priors --> posteriors)
最终代码:
#include
#include
#include
#include "helpers.h"
using std::vector;
using std::cout;
using std::endl;
vector initialize_priors(int map_size, vector landmark_positions,
float position_stdev);
float motion_model(float pseudo_position, float movement, vector priors,
int map_size, int control_stdev);
// function to get pseudo ranges
vector pseudo_range_estimator(vector landmark_positions,
float pseudo_position);
// observation model: calculate likelihood prob term based on landmark proximity
float observation_model(vector landmark_positions,
vector observations, vector pseudo_ranges,
float distance_max, float observation_stdev);
int main() {
// set standard deviation of control
float control_stdev = 1.0f;
// set standard deviation of position
float position_stdev = 1.0f;
// meters vehicle moves per time step
float movement_per_timestep = 1.0f;
// set observation standard deviation
float observation_stdev = 1.0f;
// number of x positions on map
int map_size = 25;
// set distance max
float distance_max = map_size;
// define landmarks
vector landmark_positions {3, 9, 14, 23};
// define observations vector, each inner vector represents a set
// of observations for a time step
vector > sensor_obs {{1,7,12,21}, {0,6,11,20}, {5,10,19},
{4,9,18}, {3,8,17}, {2,7,16}, {1,6,15},
{0,5,14}, {4,13}, {3,12}, {2,11}, {1,10},
{0,9}, {8}, {7}, {6}, {5}, {4}, {3}, {2},
{1}, {0}, {}, {}, {}};
// initialize priors
vector priors = initialize_priors(map_size, landmark_positions,
position_stdev);
// UNCOMMENT TO SEE THIS STEP OF THE FILTER
//cout << "-----------PRIORS INIT--------------" << endl;
//for (int p = 0; p < priors.size(); ++p){
// cout << priors[p] << endl;
//}
/**
* TODO: initialize posteriors
*/
vector posteriors(map_size, 0.0);
// specify time steps
int time_steps = sensor_obs.size();
// declare observations vector
vector observations;
// cycle through time steps
for (int t = 0; t < time_steps; ++t) {
// UNCOMMENT TO SEE THIS STEP OF THE FILTER
//cout << "---------------TIME STEP---------------" << endl;
//cout << "t = " << t << endl;
//cout << "-----Motion----------OBS----------------PRODUCT--" << endl;
if (!sensor_obs[t].empty()) {
observations = sensor_obs[t];
} else {
observations = {float(distance_max)};
}
// step through each pseudo position x (i)
for (unsigned int i = 0; i < map_size; ++i) {
float pseudo_position = float(i);
/**
* TODO: get the motion model probability for each x position
*/
float motion_prob = motion_model(pseudo_position, movement_per_timestep,
priors, map_size, control_stdev);
/**
* TODO: get pseudo ranges
*/
vector pseudo_ranges = pseudo_range_estimator(landmark_positions,
pseudo_position);
/**
* TODO: get observation probability
*/
float observation_prob = observation_model(landmark_positions, observations,
pseudo_ranges, distance_max,
observation_stdev);
/**
* TODO: calculate the ith posterior
*/
posteriors[i] = motion_prob * observation_prob;
// UNCOMMENT TO SEE THIS STEP OF THE FILTER
//cout << motion_prob << "\t" << observation_prob << "\t"
// << "\t" << motion_prob * observation_prob << endl;
}
// UNCOMMENT TO SEE THIS STEP OF THE FILTER
//cout << "----------RAW---------------" << endl;
//for (int p = 0; p < posteriors.size(); ++p) {
// cout << posteriors[p] << endl;
//}
/**
* TODO: normalize
*/
posteriors = Helpers::normalize_vector(posteriors);
// print to stdout
//cout << posteriors[t] << "\t" << priors[t] << endl;
// UNCOMMENT TO SEE THIS STEP OF THE FILTER
//cout << "----------NORMALIZED---------------" << endl;
/**
* TODO: update
*/
priors = posteriors;
// UNCOMMENT TO SEE THIS STEP OF THE FILTER
//for (int p = 0; p < posteriors.size(); ++p) {
// cout << posteriors[p] << endl;
//}
// print posteriors vectors to stdout
for (int p = 0; p < posteriors.size(); ++p) {
cout << posteriors[p] << endl;
}
}
return 0;
}
// observation model: calculate likelihood prob term based on landmark proximity
float observation_model(vector landmark_positions,
vector observations, vector pseudo_ranges,
float distance_max, float observation_stdev) {
// initialize observation probability
float distance_prob = 1.0f;
// run over current observation vector
for (int z=0; z< observations.size(); ++z) {
// define min distance
float pseudo_range_min;
// check, if distance vector exists
if (pseudo_ranges.size() > 0) {
// set min distance
pseudo_range_min = pseudo_ranges[0];
// remove this entry from pseudo_ranges-vector
pseudo_ranges.erase(pseudo_ranges.begin());
} else { // no or negative distances: set min distance to a large number
pseudo_range_min = std::numeric_limits::infinity();
}
// estimate the probability for observation model, this is our likelihood
distance_prob *= Helpers::normpdf(observations[z], pseudo_range_min,
observation_stdev);
}
return distance_prob;
}
vector pseudo_range_estimator(vector landmark_positions,
float pseudo_position) {
// define pseudo observation vector
vector pseudo_ranges;
// loop over number of landmarks and estimate pseudo ranges
for (int l=0; l< landmark_positions.size(); ++l) {
// estimate pseudo range for each single landmark
// and the current state position pose_i:
float range_l = landmark_positions[l] - pseudo_position;
// check if distances are positive:
if (range_l > 0.0f) {
pseudo_ranges.push_back(range_l);
}
}
// sort pseudo range vector
sort(pseudo_ranges.begin(), pseudo_ranges.end());
return pseudo_ranges;
}
// motion model: calculates prob of being at an estimated position at time t
float motion_model(float pseudo_position, float movement, vector priors,
int map_size, int control_stdev) {
// initialize probability
float position_prob = 0.0f;
// loop over state space for all possible positions x (convolution):
for (float j=0; j< map_size; ++j) {
float next_pseudo_position = j;
// distance from i to j
float distance_ij = pseudo_position-next_pseudo_position;
// transition probabilities:
float transition_prob = Helpers::normpdf(distance_ij, movement,
control_stdev);
// estimate probability for the motion model, this is our prior
position_prob += transition_prob*priors[j];
}
return position_prob;
}
// initialize priors assuming vehicle at landmark +/- 1.0 meters position stdev
vector initialize_priors(int map_size, vector landmark_positions,
float position_stdev) {
// set all priors to 0.0
vector priors(map_size, 0.0);
// set each landmark positon +/-1 to 1.0/9.0 (9 possible postions)
float norm_term = landmark_positions.size() * (position_stdev * 2 + 1);
for (int i=0; i < landmark_positions.size(); ++i) {
for (float j=1; j <= position_stdev; ++j) {
priors.at(int(j+landmark_positions[i]+map_size)%map_size) += 1.0/norm_term;
priors.at(int(-j+landmark_positions[i]+map_size)%map_size) += 1.0/norm_term;
}
priors.at(landmark_positions[i]) += 1.0/norm_term;
}
return priors;
}
6. 总结(Summary)
-
贝叶斯定位滤波或马尔可夫定位是递归状态估计的一般框架.
-
这意味着这个框架允许我们使用以前的状态(状态在 t-1)来估计一个新的状态(状态在 t) , 只使用当前的观测和控制(观测和控制在 t) , 而不是整个数据历史(数据从0: t).
-
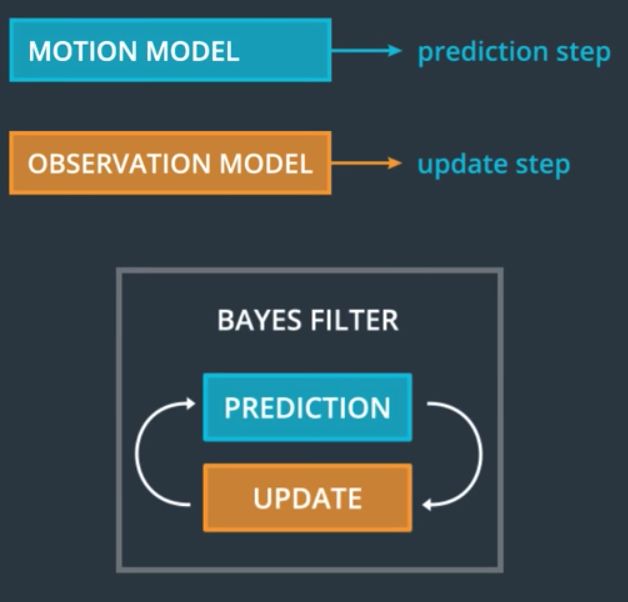
运动模型描述滤波器的预测步骤, 观测模型是更新步骤.
预测过程是利用系统模型预测状态xt的先验概率密度, 也就是通过已有的先验知识对未来系统的状态进行猜测, 更新过程是利用新的观测值zt对先验概率密度进行修正, 得到后验概率密度.
-
基于贝叶斯滤波器的状态估计依赖于预测(运动模型)和更新(观测模型步骤)之间的相互作用, 目前讨论的所有定位方法都是基于贝叶斯滤波器的实现, 比如: 一维马尔科夫定位, 卡尔曼滤波器和粒子滤波器.
引用:
- [Udacity]: www.udacity.com "Udacity"
- [Medium]: https://medium.com/intro-to-artificial-intelligence/localisation-udacitys-self-driving-car-nanodegree-8440a1f83eab "Dhanoop Karunakaran"
Linkedin: https://linkedin.com/in/williamhyin