神经网络实现手写数字识别（MNIST）

一、缘起

原本想沿着 传统递归算法实现迷宫游戏 ——> 遗传算法实现迷宫游戏 ——> 神经网络实现迷宫游戏的思路，在本篇当中也写如何使用神经网络实现迷宫的，但是研究了一下， 感觉有些麻烦不太好弄，所以就选择了比较常见的方式，实现手写数字识别（所谓的MNIST）。

二、人工神经网络简介

从小至蚂蚁（没有查到具体数目，有的说蚂蚁大脑有25万个神经细胞，也有说是50万个），大至大象，蓝鲸等动物，大脑里面都存在着大量的神经元。人或动物的各种行为或者技能，都或多或少的是因为这些由数量庞大的神经元连接而成的神经网络组成。而人工神经网络就是仿造生物的大脑来运作的，所以先来了解一笑生物的大脑（神经网络，神经元）。

2.1 生物学神经网络

先来看一个表格(来自《游戏编程中的人工智能》一书中第七章第二节，表7.1)：

动物	神经细胞数目（数量级）
蜗牛	10,000(=104)
蜜蜂	100,000（=105）
蜂雀	10, 000, 000(=107)
老鼠	100, 000, 000(=108)
人类	10, 000, 000, 000(=1010)
大象	100, 000, 000, 000(=1011)

从上表可以即便小如蜗牛也有数量庞大的神经细胞，自然界的动物需要感知环境，适应环境等等能力，就必须要有一套强大的“处理”系统来应对各种突发事件。

从人类和大象的神经细胞数量来看，是否可以推断，表现出来的智能强度，并不一定是和神经细胞的数量成正比的或者说并不是神经细胞越多就越聪明（纯属个人意见）。就好比人工神经网络，机器学习，深度学习等网络一样，并不是层数越多，神经元节点越多久越好的。

生物神经细胞如下图所示：

神经细胞之间的信号传递是通过电化学过程完成的，这些信号从一个神经细胞的轴突末梢通过突触（神经细胞轴突末梢与其他神经细胞体，树突相接触的环状或球状结构）传递给下一个神经细胞的树突，然后在从该神经细胞的树突进入细胞体，最后根据实际情况选择是否传递到下一个神经细胞。这里就需要说到神经细胞的两个状态兴奋和不兴奋（即抑制）。 神经细胞利用一种我们还不知道的方法把所有从树突进入到细胞体中的信号进行相加，如果信号总和达到某个阈值（注意：是“阈值”，yu，四声，而不是“阀值”哦，以前不知道，问了一下度娘，才知差别很大），就会激发神经细胞进入兴奋状态，这时电信号就会从当前神经细胞，通过其轴突传递向下一个神经细胞，反之则当前神经细胞就会处于抑制状态。

以上只是较为简单或单纯的神经细胞模型，在实际的大脑中电信号在神经细胞传递，不只是从一个细胞的轴突到另一个细胞的树突，还有其他的传递方向：

• 轴突——树突——细胞体
• 轴突——细胞体——树突
• 树突——细胞体——轴突

对于生物学神经网络有兴趣的可以去网上查找相应的资料，这里只是做一个简单介绍，让我们对神经细胞的基本结构以及神经冲动（电信号）传递的基本方式有一个形象的理解。重点还是人工神经网络的说明。

2.2 人工神经网络——神经细胞

人工神经网络（ANN，Artificial Neuron Network）是模拟生物大脑的神经网络结构，它是由许多称为人工神经细胞（Artificial Neuron，也称人工神经元）的细小结构单元组成。 这里的人工神经细胞可以看作是生物神经细胞的简化版本或模型。

如上图所示，就是一个人工神经细胞的示意图，其中

• x₁ … x_n：表示神经细胞的输入，也就是输入神经细胞的信号。
• w₁ … w_n：表示每个输入的权重，就好比生物神经网络中每个轴突和树突的连接的粗细，强弱的差异。
• b：偏置权重
• threshold: 偏置（可以将 threshold * b 看作是前面提到的生物神经细胞的阈值）
• 蓝色部分：细胞体。
• 黄色球形是所有输入信号以的求和。
• 红色部分是表示求和之后的信号的激励函数（即达到阈值就处于兴奋状态，反之抑制，当然作为人工神经细胞，其激励函数很多，阶跃（型）激励函数，sigmoid（s型）激励函数，双曲正切（tanh）激励函数，ReLu（Rectified Linear Units）激励函数等等）。

比较原始的感知机(如需了解什么是感知机，可问度娘)的数学表达式(或模型)如下：

$$output=\{\begin{array}{ll}0& if{\sum }_j{w}_j{x}_j<threshold\\ 1& if{\sum }_j{w}_j{x}_j\ge threshold\end{array}$$

从上面的表达式可以看出，在这里，threshold（阈值）也是神经网络的一个参数。更具体的来说，要使神经细胞处于兴奋状态（也就是上面表达式的输出一），就需要满足如下条件：
$$w_1{x}_1+w_2{x}_2+w_3{x}_3+\cdots +w_n{x}_n\ge t$$

注意: t: threshold(阈值)

网络在进行学习的过程中，人工神经网络（ANN）的所有权重都需要不断演化（进化），threshold（阈值）的数据也不应该例外，也需要做相应的演化，所以有必要将threshold（阈值）转变为权重的形式。 从上面的方程两边同时减去t得到如下形式：

$$w_1{x}_1+w_2{x}_2+w_3{x}_3+\cdots +w_n{x}_n-t\ge 0$$

这个方程还可以用另一种形式写出来，如下：
$$w_1{x}_1+w_2{x}_2+w_3{x}_3+\cdots +w_n{x}_n+tb\ge 0$$

注意：其中 b 可以取 1 或 -1， 取 1时，threshold（阈值t）取负值就可以了。

也就是说，可以将b看作一个像w的权重，将t看作像x的输入，其方程可以进一步变为：

$$w_1{x}_1+w_2{x}_2+w_3{x}_3+\cdots +w_n{x}_n+w_t{x}_b\ge 0$$

2.3 人工神经网络——神经细胞层

动物大脑里的生物神经细胞和其他神经细胞是相互连接在一起的，从而形成了庞大而复杂的神经网络。同理要创建人工神经网络（ANN），人工神经细胞也需要像生物神经细胞那样连接在一起。一个神经细胞可以看成是一个点，大量的神经细胞，就意味着大量的点，要将这些点全部连接起来，可以有很多种连接形式，其中最容易理解并且也是应用也最广泛的是：把神经细胞一层一层的连接在一起，如下图所示：

这种类型的神经网络被称为：前馈网络（feedforward network）。这是因为网络的每一层神经细胞的输出都向前馈送（feed）到他们的下一层（如上图中的从左至右的顺序），直至获得整个网络的最终输出。

由上图可知，该网络一共有3层，输入层的每个输入都馈送到了隐含层，作为该层每一个神经细胞的输入； 然后从隐含层的每个神经细胞的输出又再次馈送到它的下一层（即输出层）。

上图中只画了一个隐含层，作为前馈网络，理论上可以有任意多个隐含层，但在处理大多数问题时，通常一个隐含就足够了，而有一些更简单的问题，甚至连隐含层都不需要，直接就是一个输入层和输出层。

注意：这里只是说的简单的全连接神经网络（也就是当前层的每一个神经细胞都的输入都包含前一层的所有神经细胞的输出），对于卷积网络（CNN），，递归网络（RNN）， 生成对抗网络（GANs），深度学习，强化学习等，不在讨论的范围之内。

2.4 人工神经网络——演化

一个人工神经网络在创建之后，要能正常的工作，还是要进行一些演化（或者进化，或者学习），就像动物或者人进行学习或练习一样。对于人工神经网络来说，演化的过程就是不断的调整每一层，每一个神经细胞的输入权重。 能够调节神经网络所有神经细胞的输入权重的方式有很多，这里只说**反向传播（bp：back propagation）**法，下面就详细的说说什么是 反向传播法：

首先，我们要来了解一下，为什么网络需要演化，需要学习。答案当然就是：人工神经网络的输出结果与我们的预期不符，存在偏差。

其次，如何演化，如2.3节中的三层神经网络可知，一个神经网络可能会有很多层，每一层有很多神经细胞，每一个神经细胞都有很多输入，与这些输入对应的就是很多权重。如何才能每一个权重都被调整到呢，反向传播算法是这样做的，首先得到网络的输出层的输出与我们期望之间的误差，然后再将这个误差值反向传播到前一层（隐含层），如此往复，最后就是根据误差，学习率以及当前取值点的梯度来更新每层神经细胞的输入权重，这就是所谓的反向传播算法。而不断调整神经细胞的权重以便输出误差达到最小的过程叫做梯度下降（这是一个寻找极小值的过程，也就是寻找一个偏导数斜率最小的点）。

在百度中查了一下梯度的解释： 在单变量的实值函数的情况，梯度只是导数，或者，对于一个线性函数，也就是线的斜率。
梯度一词有时用于斜度，也就是一个曲面沿着给定方向的倾斜程度。可以通过取向量梯度和所研究的方向的点积来得到斜度。梯度的数值有时也被称为梯度。

所以寻找极小值也就是沿着梯度越来越低的方向不断搜寻，故而叫做梯度下降。

这里的梯度，就是前面提到的激活函数的导函数(不知道如何求导也没关系，因为就目前而言，常用的激活函数以及对应的导函数都可以在网上找到)，比如前向传播时，使用的激活函数是sigmoid（s型）函数：

$$f(x)=\frac{1}{1+e^{(-x)}}$$

其中：x：神经细胞所有输入（包括偏置输入）求和之后的值， f(x): 神经细胞的最终输出

其导函数为：
$$f(x{)}^{\prime }=f(x)(1-f(x))$$

换一种形式就是：
$$f(x)=x(1-x)$$

其中：x：神经细胞的输出： f(x):当前神经细胞的梯度（参见上面对梯度的解释）

下图就是使用Excel绘制的sigmoid函数以及它的导数的波形图

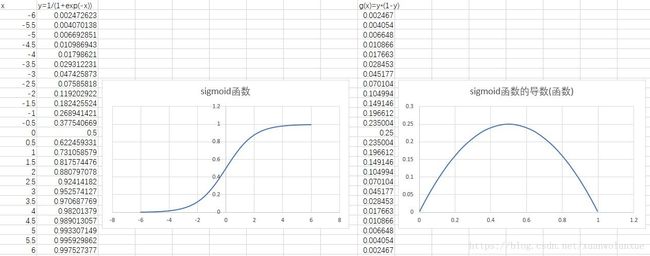
通过上面的公式，就将当前神经细胞的输出反向传播到了当前神经细胞的输入侧，而当前神经细胞的每一个输入，代表的都是反向传播方向的下一层神经细胞层的一个神经细胞。 要调整当前神经细胞的输入权重，就代表着，调整反向传播方向的下一层神经层的每一个神经细胞和当前神经细胞的连接权重。其调整幅度为：
$$\Delta W_{nj}=E_{n}L{O}_{(n-1)j}$$

其中： E： 当前神经细胞的反向传播到输入侧的误差， L：学习率， O：前一层某个神经细胞的输出，n：代表第几层神经细胞，j：代表第几个输入或者反向传播方向的下一层中的第几个神经细胞。

对于上公式中的E，在不同的神经层的计算方法略微不同（主要是输出层和隐含层的不同）

其通用计算公式为：
$$E=eo(1-o)$$

其中： e： 神经细胞的输出误差， o(1 - o): 就是前面提到的使用sigmoid激活函数时神经细胞的梯度（f(x)=x(1-x)）

这里的差异就在于 e的计算：

• 对于输出层：e = 当前神经细胞的输出 - 预期输出
• 对于隐含层：反向传播方向的上一层的所有神经细胞乘以与当前神经细胞的连接权重的累加和，其计算公式如下：

$$e=\sum _{j=0}^{j=k}{e}_{(n+1)j}{w}_{(n+1)j}$$

其中： j：表示反向传播方向的上一层的第几个神经细胞，n：表示第几层神经网络，n+1：表示在反向传播方向上当前层的上一层，e_(n+1)j： 表示反向传播的上一层的第j个神经细胞的输出误差，w_(n+1)j：表示当前神经细胞与反向传播方向的上一层的第j个神经细胞的连接权重

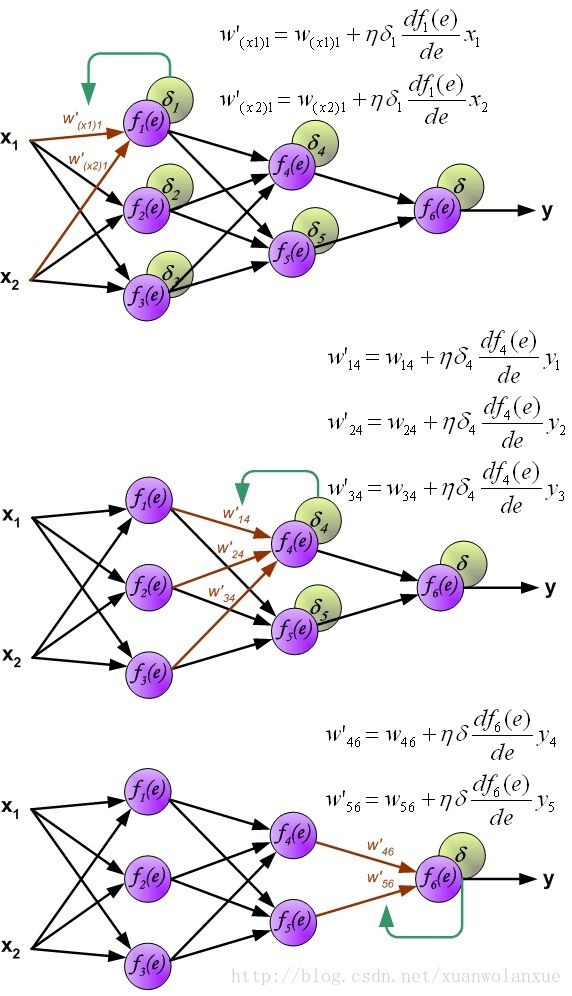
整体的反向传播算法的流程如下：

• 反向传播误差：
  

• 更新权重（正向传播）
  

上图中, $\frac{df(e)}{de}$ 就是对激活函数求导，如果使用的激活函数是sigmoid（s型函数），那么其就可以用上面的f(x)=x(1-x).

详细的信息（Principles of training multi-layer neural network using backpropagation）可以查看网站： http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html

当然还有另一种反向传播方式，和上面说到的不一样的地方是，每一层神经细胞层反向传播误差之后就计算该层每个神经细胞包含的每个输入对应的权重，然后再反向传播到下一层，再重复权重变化的计算，后面的例子当中就是使用的这种方法，目的是减少循环次数，加快训练速度。

三、手写数字识别

现在就来说说如何使用神经网络实现手写数字识别。 在这里我使用mind manager工具绘制了要实现手写数字识别需要的模块以及模块的功能：

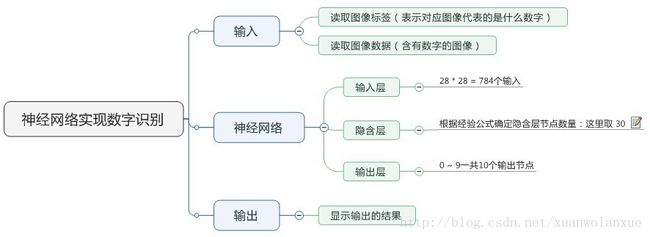
其中隐含层节点数量（即神经细胞数量）计算的公式（这只是经验公式，不一定是最佳值）：
$$m=\sqrt{n+l}+a$$
$$m={\log }_{2}n$$
$$m=\sqrt{nl}$$

• m: 隐含层节点数
• n: 输入层节点数
• l：输出层节点数
• a：1-10之间的常数

本例子当中：

• 输入层节点n：784
• 输出层节点：10 （表示数字 0 ~ 9）

隐含层选30个，训练速度虽然快，但是准确率却只有91% 左右，如果将这个数字变为100 或是300，其训练速度回慢一些，但准确率可以提高到93%~94% 左右。

因为这是使用的MNIST的手写数字训练数据，所以它的图像的分辨率是28 * 28，也就是有784个像素点，其下载地址为：http://yann.lecun.com/exdb/mnist/

这里输入和输出这两个模块都比较简单，就不用讲了，有兴趣的，在文章末尾所提供的地址去下载源码便可以详细了解。主要还是讲解神经网络这一块。

3.1 神经细胞，神经细胞层

要构建一个神经网络，那么首先就需要构建它的基本单元，神经细胞。 根据前文讲到的内容，一个神经细胞需要包含的内容为：

• 输入权重数组
• 输入数目
• 输出值
• 误差值

因为这里就是简单的bp（反向传播）神经网络，所以在同一个神经细胞层里面，每一个神经细胞的输入数目都是相同的，所以这里“输入数目”就可以省略掉，以便节省内存。 其大概形式如下：

struct neuron
{
	//int mInputCount;     /** 当前神经细胞的输入数目 */
	double mOutActivation; /** 当前神经细胞的输出 */
	double mOutError;      /** 当前神经细胞的误差 */
	vector<double> mWeights; /** 当前神经细胞的输入权重数组 */
};

同理推断神经细胞层的结构为：

struct neuronLayer
{
	int mNumInputsPerNeuron; /** 当前层的每个神经细胞的输入数目 */
	int mNumNeurons; /** 当前层的神经细胞数目 */
	vector<neuron> mNeurons; /** 当前层的神经细胞数组 */
};

但是为了简化结构，方便计算，在本例子当中，省略了神经细胞（neuron）这个结构，直接定义神经细胞层，在神经细胞层里面分别使用数组来存放神经细胞（neuron）结构里面的成员变量，如下所示：

/** the type of neuron layer */

struct neuronLayer 
{
public:
	neuronLayer(int numNeurons, int numInputsPerNeuron); /** 神经细胞层的构造函数*/

	neuronLayer(neuronLayer& nl); /** 神经细胞层的拷贝构造函数 */
	~neuronLayer(); /** 神经细胞层的析构函数 */

	void reset(void); /** 神经细胞层的重置函数（将权重等参数都重置为随机值）*/
public:
	int mNumInputsPerNeuron; /** 当前层的每个神经细胞的输入数目 */
	int mNumNeurons; /** 当前层的神经细胞数目 */
	double** mWeights; /** 2维数组, 行: 代表神经细胞（每一行就是一个神经细胞的所有权重）, 列: 代表神经细胞的输入权重 */
	double* mOutActivations; /** 当前层每个神经细胞的输出值 */
	double* mOutErrors; /** 当前层每个神经细胞的误差值 */

};

有了神经细胞层，接下来就该是实现神经网络了。

3.2 神经网络

本例子特征：

• 简单的全连接神经网络；
• 层数可自定义；
• 每一个隐含层的神经细胞数目可自定义；
• 使用反向传播以及梯度下降法进行网络演化；
• 激励函数使用：sigmoid（S型）函数；
• 使用c++语言实现。

首先来看一下，神经网络类的数据结构：

class bpNeuronNet
{
public:
	bpNeuronNet(int numInputs, double learningRate); /** 构造函数 */
	~bpNeuronNet(); /** 析构函数 */
public:
	/** 或者网络的总误差（输出层每个神经细胞输出误差的方差总和） */
	inline double getError(void) { return mErrorSum; } 

	bool training(const double inputs[], const double targets[]); /** 训练网络 */
	void process(const double inputs[], double* outputs[]); /** 处理数据（这里是数字识别） */

	void reset(void); /** 重置网络 */
	void addNeuronLayer(int numNeurons); /** 添加一个神经网络层 */

private:

	/** 前向传播，计算网络的输出 */
	
	/** sigmoid(S型)激活函数 */
	inline double sigmoidActive(double activation, double response); 
	
	/** 更新一个神经网络层，计算其输出 */
	void updateNeuronLayer(neuronLayer& nl, const double inputs[]); 

	/** 反向传播，训练网络 */

        /** 反向传播的激活函数，sigmoid函数的导数 */
	inline double backActive(double x);

        /** 以训练模式更新网络，与 process 函数的区别是，这个函数会更新输出层的每个神经细胞的输出误差 */
	void trainUpdate(const double inputs[], const double targets[]);

	/** 训练一层神经细胞层 */
	void trainNeuronLayer(neuronLayer& nl,  const double prevOutActivations[], 
						  double prevOutErrors[]);

private:
	int mNumInputs; /** 神经网络的输入数目 */
	int mNumOutputs; /** 神经网络的输出数目 */
	/** 隐含层数目，总的神经网络层的数目= mNumHiddenLayers + 1
	* （不包含输入层，因为它是直接映射到第一个隐含层，没有神经细胞 ） */
	int mNumHiddenLayers;
 	/** 神经网络的学习率（表示学习速度的），需要慎重选择，太大会出现错误收敛或者无法收敛，
	* 太小也可能导致错误收敛，且学习速度变慢 */
	double mLearningRate; 
	double mErrorSum; /** 忘了总误差，参看：getError函数 */
	vector<neuronLayer*> mNeuronLayers; /** 神经网络包含的神经细胞层数组 */
};

上面的类的成员函数的各个参数应该都能够自解释，再加上中文注释，应该就不需要再多说什么了。

注意：因为输入层，都是将数据直接映射到第一个隐含层，所以，它没有神经细胞，这也是为什么在2.3节中三层神经网络结构图中，输入层是绿色的正方形，而不是后面两层那样的圆形。 所以对于输入层不需要调用addNeuronLayer 函数进行添加，在构造神经网络时，已经使用numInputs参数传入到神经网络了。

这里这些成员函数的具体实现：

正向传播方向的函数：

• 比较简单的 sigmoid（S型）函数，公式前面已经说过了，代码实现如下：

double bpNeuronNet::sigmoidActive(double activation, double response)
{/** reponse 是用于缩放 activation的，取值范围： 0 < response <= 1.0 */
	/** sigmoid function: f(x) = 1 /(1 + exp(-x)) */
	return (1.0 / (1.0 + exp(-activation * response)));
}

这里多了一个response参数，其实它用来对当前神经细胞所有输入信号（包括偏置）的累加和进行缩放的，前面2.4节中有关于sigmoid函数的波形图，可以看到，x的取值负的越小，或者正的越大的时候，就越是逼近 0 或 1（可称他们为极值或者饱和区），而且曲线也平缓，根据前面说到的在训练时，反向传播是sigmoid函数的导数，也就是sigmoid曲线上的点相对应的斜率（而这个斜率又是相应的梯度），当逼近饱和区时，因为曲线变得平缓，斜率就趋近于0，这样对于得到的权重变化就会非常非常小，也趋近于0， 也就是几乎达不到演化神经网络的目的（因为权重基本上没什么变化，就没有调整权重的意义了）， 所以调整这个值也可以改变学习度，影响识别率，有兴趣的可以试试。

• updateNeuronLayer函数，利用传入的inputs数据更新一个神经细胞层的输出数据：

void bpNeuronNet::updateNeuronLayer(neuronLayer& nl, const double inputs[])
{
	int numNeurons = nl.mNumNeurons; /** 当前层有多少个神经细胞 */
	int numInputsPerNeuron = nl.mNumInputsPerNeuron; /** 当前层的每一个神经细胞有多少输入 */
	double* curOutActivations = nl.mOutActivations; /** 当前层所有神经细胞的输出值数组 */

	/** 遍历每一个神经细胞 */
	for (int n = 0; n < numNeurons; ++n)
	{
		double* curWeights = nl.mWeights[n]; /** 获取第n个神经细胞的输入权重数组 */

		double netinput = 0;
		int k;
		/** 遍历每一个输入权重 */
		for (k = 0; k < numInputsPerNeuron; ++k)
		{
			/*** 累加 weights 和 inputs的乘积 */
			netinput += curWeights[k] * inputs[k];
		}

		/** 添加偏置项的值 */
		netinput += curWeights[k] * BIAS;


		/** 将累加后的值通过激活函数，得到当前神经细胞的最终输出 */
		curOutActivations[n] = sigmoidActive(netinput, ACTIVATION_RESPONSE);
	}
}

这个函数中有连个宏定义，ACTIVATION_RESPONSE是介绍sigmoidActive函数时已经说过的，这里不再多说，然后就是BIAS，这个就是偏置输入，可以取1或者-1， 当取值为1时，其实这个宏就可以取消掉。

• process，数据处理函数，处理输入数据（本例是识别手写数字），得到相应输出

void bpNeuronNet::process(const double inputs[], double* outputs[])
{
	/** 逐层更新网络 */
	for (int i = 0; i < mNumHiddenLayers + 1; i++)
	{
		updateNeuronLayer(*mNeuronLayers[i], inputs);
		inputs = mNeuronLayers[i]->mOutActivations;
	}

	/** 获取输出层的神经细胞的输出数组（即整个网络的最终输出结果）*/
	*outputs = mNeuronLayers[mNumHiddenLayers]->mOutActivations;

}

此函数比较加单，就是正向的从：输入层（inputs参数）——>第一隐含层——>…——>输出层，逐层更新网络，并将每一层的结果馈送到下一层（前馈网络）。

以下就是反向传播方向（训练神经网络）的相关函数：

• backActive函数，之前说到的sigmoid函数的导数：

double bpNeuronNet::backActive(double x)
{
	/** 
	* f(x) = x * (1 - x) sigmoid函数的导数
	*/
	return x * (1 - x);
}

• trainUpdate，以训练模式更新网络的函数

void bpNeuronNet::trainUpdate(const double inputs[], const double targets[])
{
	for (int i = 0; i < mNumHiddenLayers + 1; i++)
	{/** 调用updateNeuronLayer函数，正向传播方向，循环的逐层更新网络 */
		updateNeuronLayer(*mNeuronLayers[i], inputs);
		inputs = mNeuronLayers[i]->mOutActivations;
	}

	/** 获取网络的输出层 */
	neuronLayer& outLayer = *mNeuronLayers[mNumHiddenLayers];
	double* outActivations = outLayer.mOutActivations; /** 输出层的神经细胞的输出数字 */
	double* outErrors = outLayer.mOutErrors; /** 输出层的神经细胞的输出误差数组 */
	int numNeurons = outLayer.mNumNeurons; /** 输出层的神经细胞数量 */
	
	mErrorSum = 0; /** 重置整个网络的总误差 */
	/** 更新输出层神经细胞的输出误差 */
	for (int i = 0; i < numNeurons; i++)
	{
		//double err =  outActivations[i] - targets[i]; 
		double err = targets[i] - outActivations[i]; /** 获取误差 */
		outErrors[i] = err; /** 保存误差 */
		/** 更新方差累加和. (当这个值比预设的阈值小的时候，就可以代表网络已经训练成功了)  */
		mErrorSum += err * err;
	}
}

• trainNeuronLayer 训练一层神经细胞层

void bpNeuronNet::trainNeuronLayer(neuronLayer& nl, const double prevOutActivations[], 
                                   double prevOutErrors[])
{
	int numNeurons = nl.mNumNeurons; /** 当前层的神经细胞数目 */
	int numInputsPerNeuron = nl.mNumInputsPerNeuron; /** 当前层每个神经细胞的输入数目 */
	double* curOutErrors = nl.mOutErrors; /** 当前层神经细胞的输出误差数组 */
	double* curOutActivations = nl.mOutActivations; /** 当前层的神经细胞的输出数组 */

	/** 遍历当前层的神经细胞，并计算每个神经细胞的输出误差以及调整权重的依据 */

	for (int i = 0; i < numNeurons; i++)
	{
		double* curWeights = nl.mWeights[i]; /** 获取当前神经细胞的输入权重数组 */
		double coi = curOutActivations[i]; /** 获取当前神经细胞的输出 */
		/** 利用反向传播激活函数计算反向传播回来的误差 */
		double err = curOutErrors[i] * backActive(coi);

		/** 遍历当前神经细胞的所有权重，并基于反向传播回来的误差和学习率等参数计算新的权重值 */

		int w;
		/** 遍历当前神经细胞的权重，不包括偏置项 */
		for (w = 0; w < numInputsPerNeuron; w++)
		{
			/** 更新反向传播到，反向传播方向的下一层相应神经细胞的输出误差 */
			if (prevOutErrors) 
			{/** 因为输入层只有数据，没有神经细胞，所以此处需要判断此数组是否存在 */
				prevOutErrors[w] += curWeights[w] * err;
			}	

			/** 基于反向传播规则计算新的权重 */
			curWeights[w] += err * mLearningRate * prevOutActivations[w];
		}

		/** 更新当前神经细胞偏置项的权重 */
		curWeights[w] += err * mLearningRate * BIAS;
	}
}

trainNeuronLayer函数中计算新权重的规则处，“curWeights[w] += err * mLearningRate * prevOutActivations[w];”， 这里使用的是 “+=” ，这一点是需要和trainUpdate函数中“double err = targets[i] - outActivations[i];”相对应的，也就是说当 “err = t - o;” 获取误差时，需要使用“+=”（加等于），当使用“err = o - t;”时，需要使用" -= "(减等于)

• training，训练函数，根据输入数据，与预期结构对神经网络进行训练（演化）：

bool bpNeuronNet::training(const double inputs[], const double targets[])
{
	const double* prevOutActivations = NULL;
	double* prevOutErrors = NULL;
	trainUpdate(inputs, targets); /** 以训练模式更新网络 */

	/** 以反向传播方向的顺序逐层训练网络 */
	for (int i = mNumHiddenLayers; i >= 0; i--)
	{
		neuronLayer& curLayer = *mNeuronLayers[i]; /** 获取第i层神经细胞层 */

		/** get the out activation of prev layer or use inputs data */

		if (i > 0)
		{
			/** 获取反向传播方向上的下一层神经细胞层 */
			neuronLayer& prev = *mNeuronLayers[(i - 1)];
			/** 获取反向传播方向上的下一层的神经细胞的输出数组 */
			prevOutActivations = prev.mOutActivations; 
			/** 获取反向传播方向上的下一层的神经细胞的输出误差数组 */
			prevOutErrors = prev.mOutErrors;
			/** 重置获取反向传播方向上的下一层的神经细胞的输出误差为 “0” */
			memset(prevOutErrors, 0, prev.mNumNeurons * sizeof(double));

		}
		else
		{
		/** i=0时，表示第一层隐含层，它的输入就是整个网络的输入数据（即所谓的输入层） */
			prevOutActivations = inputs;
			prevOutErrors = NULL;
		}

		/** 调用trainNeuronLayer函数训练第i层神经细胞 */
		trainNeuronLayer(curLayer, prevOutActivations, prevOutErrors);
	}

	return true;
}

自此，神经网络的正向和反向的相关成员函数都已介绍完毕，整体上来说，代码不多，理解了原理，也就不难理解这些代码了，接下来就是介绍神经网络识别手写数字的测试程序（包括训练和测试识别）

3.3 神经网络识别手写数字测试程序

不说废话，直接进入主题。首先来看训练函数：

double trainEpoch(dataInput& src, bpNeuronNet& bpnn, int imageSize, int numImages)
{
	double net_target[NUM_NET_OUT]; /** 存放网络的预期输出 */
	char* temp = new char[imageSize]; /** 创建临时数组来存放读取的手写数字的图像 */
	progressDisplay progd(numImages); /** 显示进度的工具类 */

	double* net_train = new double[imageSize];  /** 存放网络输入数据 */
	for (int i = 0; i < numImages; i++)
	{
		int label = 0;
		memset(net_target, 0, NUM_NET_OUT * sizeof(double));

		if (src.read(&label, temp)) /** 读取一张手写数字的图像和代表这个图像中数字的标签 */
		{
			net_target[label] = 1.0; /** 将标签对于的预期输出位置 1 */

			/**预处理手写数字图像数据为网络输入数据，并添加相应的噪声 */
			preProcessInputDataWithNoise((unsigned char*)temp, net_train, imageSize);
                        /** 训练网络 */
			bpnn.training(net_train, net_target);

		}
		else
		{
			cout << "read train data failed" << endl;
			break;
		}
		//progd.updateProgress(i);

		progd++; /** 更新训练进度 */
	}

	cout << "the error is:" << bpnn.getError() << " after training " << endl;

	delete []net_train;
	delete []temp;

	return bpnn.getError();
}

上面函数中，预处理手写数字图像数据时，之所以加入噪声，是为了防止过拟合（至于什么是过拟合，还请询问度娘去）的一种技巧，添加摇摆（jitter）。《游戏编程中的人工智能》一书的第九章第三节有讲到。

然后是测试识别函数：

int testRecognition(dataInput& testData, bpNeuronNet& bpnn, int imageSize, int numImages)
{
	int ok_cnt = 0;
	double* net_out = NULL;
	char* temp = new char[imageSize];/** 创建临时数组来存放读取的手写数字的图像 */
	progressDisplay progd(numImages);/** 显示进度的工具类 */
	double* net_test = new double[imageSize]; /** 存放网络输入数据 */
	for (int i = 0; i < numImages; i++)
	{
		int label = 0;

		if (testData.read(&label, temp))/** 读取一张手写数字的图像和代表这个图像中数字的标签 */
		{		
			/** 预处理手写数字图像数据 */	
			preProcessInputData((unsigned char*)temp, net_test, imageSize);

			/**利用神经网络处理（识别） 手写数字图像数据 */
			bpnn.process(net_test, &net_out);


			/** 遍历神经网络的所有输出，找出最大的一个 */
			int idx = -1;
			double max_value = -99999;
			for (int i = 0; i < NUM_NET_OUT; i++)
			{
				if (net_out[i] > max_value)
				{
					max_value = net_out[i];
					idx = i;
				}
			}

			if (idx == label) 
			{/** 如果最大输出对应的神经细胞的idx与读取的数字对应的标签相等，表示识别成功，计数加1 */
				ok_cnt++;
			}

			progd.updateProgress(i); /** 更新识别进度 */
		}
		else
		{
			cout << "read test data failed" << endl;
			break;
		}
	}


	delete []net_test;
	delete []temp;

	return ok_cnt;

}

以上函数中，之所以要遍历神经网络的输出，找到最大的一个，是因为我们使用的激活函数（sigmoid函数）：
$$f(x)=\frac{1}{1+e^{(-x)}}$$

要得到1， 必须x取正无穷大，这显然不现实。 所以只能找最接近 1的一个输出，作为网络的有效输出。

最后简单的看一下main函数：

int main(int argc, char* argv[])
{
	dataInput src; /** 用于训练神经网络的数据读取对象 */
	dataInput testData; /** 用于测试识别的数据读取对象 */
	bpNeuronNet* bpnn = NULL;
	srand((int)time(0));

	if (src.openImageFile("train-images.idx3-ubyte") && 
	    src.openLabelFile("train-labels.idx1-ubyte"))
	{/** 打开手写数字图像数据文件以及对应的标签文件 */
		int imageSize = src.imageLength(); /** 获取一张手写数字图像的大小（像素总和）*/
		int numImages = src.numImage(); /** 获取数据集有多少张图像 */
		int epochMax = 1;

		double expectErr = 0.1;

		bpnn = new bpNeuronNet(imageSize, NET_LEARNING_RATE); /** 创建神经网络 */

		/** add first hidden layer */

		bpnn->addNeuronLayer(NUM_HIDDEN); /** 添加隐含层 */
		
		/** add output layer */
		bpnn->addNeuronLayer(NUM_NET_OUT);  /** 添加输出层 */

		cout << "start training ANN..." << endl;

		/** 训练网络 */
		for (int i = 0; i < epochMax; i++)
		{
			double err = trainEpoch(src, *bpnn, imageSize, numImages);

			//if (err <= expectErr)
			{
			//	cout << "train success,the error is: " << err << endl;
			//	break;
			}

			src.reset();
		}

		cout << "training ANN success..." << endl;

		showSeparatorLine('=', 80);
		
		if (testData.openImageFile("t10k-images.idx3-ubyte") && 
		    testData.openLabelFile("t10k-labels.idx1-ubyte"))
		{/**打开用于测试识别的手写数字图像数据以及相应的标签数据 */
			imageSize = testData.imageLength();/** 获取一张手写数字图像的大小（像素总和）*/
			numImages = testData.numImage();/** 获取数据集有多少张图像 */
			
			cout << "start test ANN with t10k images..." << endl;

			/** 测试识别 */
			int ok_cnt = testRecognition(testData, *bpnn, imageSize, numImages);

			cout << "digital recognition ok_cnt: " << ok_cnt << ", total: " << numImages << endl;
		}
		else
		{
			cout << "open test image file failed" << endl;
		}


	}
	else
	{
		cout << "open train image file failed" << endl;
	}

	if (bpnn)
	{
		delete bpnn; /** 销毁神经网络 */
	}

	getchar();

	return 0;
}

注意：addNeuronLayer函数，必须按照正向传播方向的顺便添加，即 第一隐含层——>…——>第n隐含层——>输出层，这样的顺序。

四、总结与后续

神经网络的原理虽然看上去不难，但实现起来还是不太简单，这还是最简单的神经网络，如果是CNN，RNN，深度网络等等那就更加复杂了，且参数之多，也是难以想象的。

第三章的例子还是只比较粗糙的版本，后续还可以添加更多的功能，比如：

• 将宏定义和网络层数等进行参数化，外部使用ini文件之类的配置文件，测试程序读取这些配置就可以构建和初始化神经网络。
• 在神经网络类中添加成员函数来提取和设置所有神经细胞的输入权重，这样一个训练好的神经网络，就可以将权重提取出来，保存为一个配置文件，下次就可以直接读取配置文件来初始化权重，这样就不需要每次使用的时候都要先对网络进行演化。
• 使用遗传算法来演化网络中神经细胞的权重，然后再使用反向传播来训练网络。
• 。。。

一个简单的神经网络的基本知识就是这些了，下一步就需要研究研究 深度学习之类的东东了。

五、完整代码

完整代码时放在开源中国上面，有兴趣的可以抓取来瞧一瞧。其地址如下：

https://gitee.com/xuanwolanxue/digital_recognition_with_neuron_network.git

六、更新

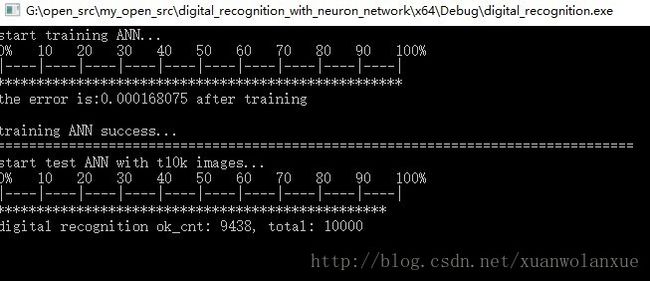
添加上程序运行之后的识别结果，如下图所示：

从上图可以看出， 使用10000个样本，最后正确识别的为9438个， 正确识别率为94.38%。

[2018年8月7日更新]：在原有的基础上增加了训练和测试各自的用时时间，其结果如下所示：