异常检测:局部异常因子LOF算法在python中实现
原文:http://kakazai.cn/index.php/Kaka/Jqxx/query/id/6
文章目录
- 一、别名
- 二、历史
- 三、算法简介
- (1)核心思想
- (2)算法描述
- (3)时间复杂度分析
- 四、算法的变种
- (1)FastLOF
- 五、LOF在sklearn中的有关函数
- 核心函数LocalOutlierFactor
- 函数model.fit()
- 函数model.kneighbors()
- 函数model._decision_function()
- 函数model._predict(x)
- 六、代码
- 七、应用领域
- (1)工程应用领域
- (2)自然生态应用领域
- (3)公共服务领域
- 参考
一、别名
Local Outlier Factor、LOF
局部异常因子算法
二、历史
Local Outlier Factor(LOF)是基于密度的经典算法,由慕尼黑大学的Markus M. Breunig等发表在2000年的数据库顶级会议SIGMOD上,论文为《LOF: Identifying Density-Based Local Outliers》。
LOF旨在发现数据集中的异常模式。在LOF之前,对异常的认知是非黑即白的,一个样本点要不是正常点,要不是异常点。而Breunig等想量化每个样本点的异常程度,并认为这取决于样本点跟周围邻居的密度对比。LOF的核心思想是,异常与否,取决于局部环境,因而被命名为”局部异常因子算法”。
LOF的优点在于它简单,直观,不需要知道数据集的分布,并能量化每个样本点的异常程度。
三、算法简介
(1)核心思想
局部密度:LOF认为,某个样本点p的第k个最近邻居越近,表明靠近它的邻居越多,它的局部密度越大;反之,第k个最近邻居越远,它的局部密度越小。因此,LOF将样本点p的局部密度定义为第k个最近邻居的距离的倒数。
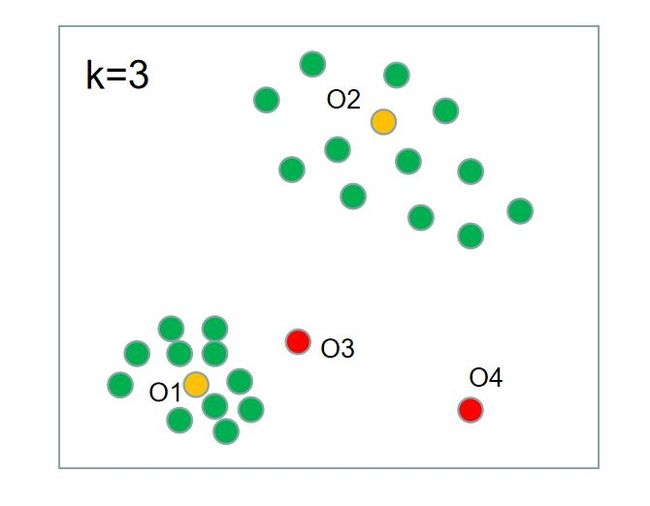
如下图所示,O1的局部密度明显比O2的局部密度大,而O1的第k个邻居确实比O2的来得更近。
异常程度:p异常与否,并不是取决于p的局部密度,而取决于p的局部密度与邻居们的局部密度的对比。比如,p的局部密度虽然小,但它的邻居们局部密度都很小,那么p的异常程度就很低。反而,p的局部密度小,邻居们的局部密度都很大,那么p的异常程度就很高。
如下图所示,O2的局部密度虽小,但我们不会认为O2异常,因为O2的邻居们的局部密度也差不多大小。O3的局部密度跟O2的差不多,但O3却显得异常,因为O3的邻居们局部密度都比O3大。
(2)算法描述
备注:这里只考虑用LOF算法来判断原有数据集中的异常情况,不考虑预测新数据的异常情况。若加入新数据,则局部密度的计算是另一种方案。
S1 计算出所有样本点的局部密度
计算出所有其他点到样本点p的距离,升序排列,取第k个距离为k-distance;
样本点p的局部密度ρ=1/k-distance;
注意:若有k个或以上的点跟p重合,即到p的距离是0,则ρ无法计算,要排除这种情况。或者,k-distance都加上一个很小的值,避免ρ无法计算。
S2 计算出所有样本点的异常分数
记所有离样本点p的距离小于等于k-distance的点的集合为N,即p的k-distance以内的邻居们;
计算出N中所有点的局部密度,并取其平均值,记为ρ-mean;
样本点p的异常分数score = ρ-mean/ρ;
S3 分析异常程度
若异常分数接近1,则说明样本点p的局部密度跟邻居的接近。
若异常分数小于1,表明p处于一个相对密集的区域,不像一个异常点。
若异常分数远大于1,表明p跟其他点比较疏远,很可能是一个异常点。
(3)时间复杂度分析
LOF算法要计算样本点两两之间的距离,时间复杂度是O(n^2)。
四、算法的变种
(1)FastLOF
为了提高算法效率,后续有算法尝试改进。FastLOF (Goldstein,2012)先将整个数据随机的分成多个子集,然后在每个子集里计算 LOF 值。对于那些 LOF 异常得分小于等于 1 的,从数据集里剔除,剩下的在下一轮寻找更合适的 nearest-neighbor,并更新 LOF 值。这种先将数据粗略分成多个部分,然后根据局部计算结果将数据过滤来减少计算量的想法,并不罕见。比如,为了改进 K-means 的计算效率, Canopy Clustering 算法也采用过比较相似的做法。
五、LOF在sklearn中的有关函数
sklearn中已经实现了LOF算法,其模型函数是LocalOutlierFactor()。
核心函数LocalOutlierFactor
#函数中的参数值皆为默认值
class sklearn.neighbors.LocalOutlierFactor(n_neighbors=20, algorithm=’auto’, leaf_size=30, metric=’minkowski’, p=2, metric_params=None, contamination=’legacy’, novelty=False, n_jobs=None)
参数说明
(1)n_neighbors int型参数;取离样本点p第k个最近的距离,k=n_neighbors
(2)algorithm='auto' str参数;即内部采用什么算法实现,['auto', 'ball_tree', 'kd_tree', 'brute']。
'brute':暴力搜索;默认'auto':自动根据数据选择合适的算法。一般低维数据用kd_tree速度
快,用ball_tree相对较慢。超过20维的高维数据用kd_tree效果不佳,而ball_tree效果好。
(3)leaf_size int参数;基于以上介绍的算法,此参数给出了kd_tree或者ball_tree叶节点规模,叶节点的
不同规模会影响数的构造和搜索速度,同样会影响储树的内存的大小。
(4)contamination 设置样本中异常点的比例,默认为 0.1
(5)metric str参数或者距离度量对象;即怎样度量距离。默认是闵氏距离minkowski。
(6)p int参数;就是以上闵氏距离各种不同的距离参数,默认为2,即欧氏距离。p=1代表曼哈顿距离等
(7)metric_params 距离度量函数的额外关键字参数,一般不用管,默认为None。
(8)n_jobs int参数;并行任务数,默认为1表示一个线程,设置为-1表示使用所有CPU进行工作。可以指定为
其他数量的线程。
(9)novelty
函数model.fit()
model.fit(data) #data为数据集,fit表示对模型进行训练
函数model.kneighbors()
model.kneighbors(data) #获取k距离邻域内,每个点到中心点的距离,并升序排列
返回值
返回一个元组,包含两个多维数组。第一个n*k数组是每个样本点的最近k个距离;第二个n*k数组是每个样本点的最近k个距离对应的点索引
函数model._decision_function()
model._decision_function(data) #返回data数据集的每个样本点的异常分数,是一个负数
函数model._predict(x)
model._predict(data) #返回data数据集的每个元素的样本点异常与否,正常是1,异常是-1
六、代码
#导入鸢尾花数据集
from sklearn import datasets #导入内置数据集模块
iris=datasets.load_iris() #导入鸢尾花的数据集
x=iris.data[:,0:2] #样本数据共150个,取前两个特征,即花瓣长、宽
#可视化数据集
import matplotlib.pyplot as plt
plt.scatter(x[:,0],x[:,1]) #x的第0列绘制在横轴,x的第1列绘制在纵轴
plt.show()
#训练模型
from sklearn.neighbors import LocalOutlierFactor
model = LocalOutlierFactor(n_neighbors=4, contamination=0.1) #定义一个LOF模型,异常比例是10%
model.fit(x)
#预测模型
y = model._predict(x) #若样本点正常,返回1,不正常,返回-1
#可视化预测结果
plt.scatter(x[:,0],x[:,1],c=y) #样本点的颜色由y值决定
plt.show()
#模型其他指标
temp1 = model.kneighbors(x) #找出每个样本点的最近k个邻居,返回两个数组,一个是邻居的距离,一个是邻居的索引
temp2 = temp1[0] #k个最近邻居的距离
temp3 = temp1[1] #k个最近邻居在样本中的序号
temp3 = temp2.max(axis=1) #取最大值,即第k个邻居的距离
temp4 = -model._decision_function(x) #得到每个样本点的异常分数,注意这里要取负
七、应用领域
(1)工程应用领域
数据清洗:在做特征工程和模型训练之前对数据进行清洗,剔除无效数据和异常数据。
欺诈检测:信用卡的不正当行为,如信用卡、社会保障的欺诈行为或者是银行卡、电话卡的欺诈使用等
工业检测:如计算机网络的非法访问等
活动监控:通过实时检测手机活跃度或者是股权市场的可疑交易,从而实现检测移动手机诈骗行为等
网络性能:计算机网络性能检测(稳健性分析),检测网络堵塞情况等
(2)自然生态应用领域
生态系统失调、异常自然气候的发现等
(3)公共服务领域
公共卫生中的异常疾病的爆发、公共安全中的突发事件的发生等
参考
https://zhuanlan.zhihu.com/p/37753692 LOF离群因子检测算法及python3实现
https://blog.csdn.net/bbbeoy/article/details/80301211 机器学习-异常检测算法(二):Local Outlier Factor
https://blog.csdn.net/u010536377/article/details/50525785 [数据挖掘]离群点检测—基于kNN的离群点检测、LOF算法和CLOF算法
http://www.cnblogs.com/bonelee/p/9848019.html [异常检测——局部异常因子(Local Outlier Factor ,LOF)算法]
https://blog.csdn.net/qq_43104025/article/details/82346403 局部异常因子算法-Local Outlier Factor(LOF)
https://blog.csdn.net/YE1215172385/article/details/79766906 异常检测(三)——Local Outlier Factor(LOF)
M. M. Breunig, H. P. Kriegel, R. T. Ng, J. Sander. LOF: Identifying Density-based Local Outliers. SIGMOD, 2000.
M. Goldstein. FastLOF: An Expectation-Maximization based Local Outlier detection algorithm. ICPR, 2012