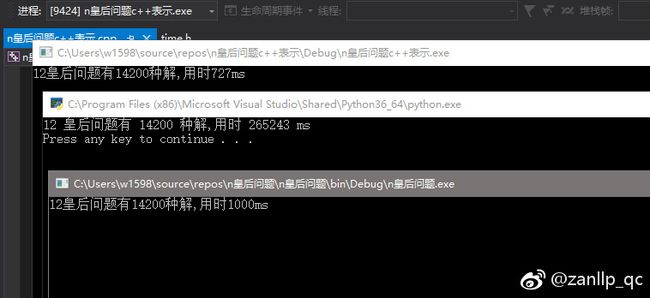
用回溯法解决八皇后问题的思路,并求出17皇后解的数量(c#,c++,python表示)
1.解决思路
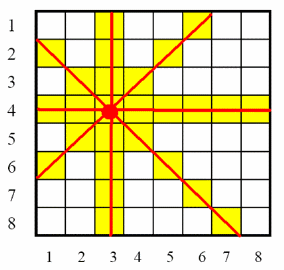
借用网上一张图,中间那个红点表示的就是皇后,这图的意思也就是一个皇后的影响范围为这这个皇后所在的那一列,那一行,对角线以及次对角线。其它的皇后不能在它的影响范围里否则会冲突。八皇后也就是在一个8x8的棋盘上后置8个皇后,皇后的数量与棋盘的行列数一样。这是基础,再来说说回溯法,回溯法最重要的思想就是当前这一步走不通,我们就掉头返回上一步找其他方案。这相对于枚举法列出所有可能再逐个进行排除要节省资源的多。
首先皇后的冲突规则是在同一行,同一列,同一对角线,同一次对角线。因为多个皇后不可能在同一行,所以我们可以看成第一个皇后在第一行,第二个皇后在第二行.........再用一个值来表示数组来表示皇后是处于第几列的,那么某个皇后在棋盘上的位置就可以用这是第几个皇后表示y,这个皇后对应数组里的值表示x。并且这样对于检测冲突可以少对比一次,只需要检测时候是否处于同一列,同一对角线,同一次对角线即可。
再来说说回溯法在n皇后问题上的应用,在棋盘上我们可以先放第一个皇后,再放一个皇后再检验冲突,如果遇到冲突将这个皇后的位置向右移动,如果这个皇后移动超出了棋盘,这表明这种情况下没有解,对此可以把这个皇后拿出棋盘并移动上一个皇后,直到上一个皇后也不冲突,在继续放置下一个皇后,找出不冲突的位置,如果到了就这样放到了第八个皇后仍不冲突那么得到一种解。在得到了一种解后再把第8个皇后拿出棋盘,移动第7个皇后,继续找出不冲突的位置,如果第7个皇后剩下的位置全冲突,那把第7个皇后拿出棋盘,再移动第6个皇后的位置........就酱,如果第一个皇后移动超出了棋盘那么表示已经找出所有解。
2.代码
using System;
namespace n皇后问题
{
class Program
{
static int Queen_n =12;//皇后数量
static int[] queens = new int[Queen_n];//保存所有皇后的位置
static int QueenSolution_n = 0;//有多少解
static double time = 0;
static void Main(string[] args)
{
time = Environment.TickCount;//记录程序启动时间
for (int i = 0; i < Queen_n; i++)//对所有皇后初始化
{
queens[i] = 0;
}
nQueen(0);
Console.WriteLine(Queen_n + "皇后问题有" + QueenSolution_n + "种解,用时"+(Environment.TickCount-time)+"ms");
Console.ReadKey();
}
static bool IS = false;
static void nQueen(int now)
{
for (int i = now; i < Queen_n; i++)
{
while (IsConlict(i) || queens[i] >= Queen_n)//如果当前皇后的位置与前几个冲突,或者超出棋盘,进来返回上一层
{
queens[i]++;//皇后位置右移
if (queens[i] >= Queen_n)//如果这皇后没有结果
{
if (queens[0] >= Queen_n)//第一个皇后越界,结束
{
return;
}
queens[i] = 0;//当前皇后位置归0
i--;//返回上一个皇后
queens[i]++;//当前皇后位置右移
nQueen(i);//
return ;//释放
}
}
if (i == Queen_n - 1)//如果到了第八个皇后,且不冲突。得到一种解
{
//Console.WriteLine("解+1,目前是第"+QueenSolution_n);
queens[i] = 0;//当前皇后位置归0
i--;//返回上一个皇后
queens[i]++;//当前皇后位置右移
QueenSolution_n++;//解+1
nQueen(i);
return;
}
}
}
static bool IsConlict(int now)//当前是第now个皇后,一个皇后占一行,所以它是第几个皇后也就表示,这个皇后在第几行
{
for (int i = 0; i < now; i++)
{//在同一对角线,在同一斜对角线,在同一列上
if (((i - now) == (queens[i] - queens[now])) || ((i - now) == -(queens[i] - queens[now])) || (queens[i] == queens[now]))
{
return true;//冲突
}
}
return false;
}
}
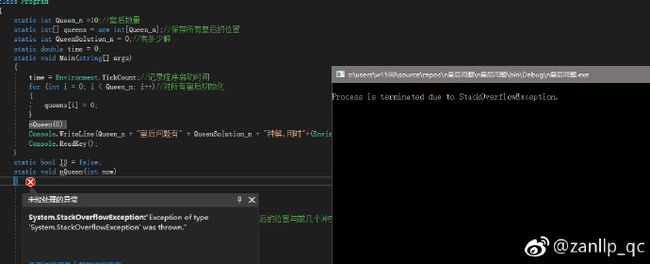
}但是
这是由于递归太多导致的栈溢出,对此可以改变思路不是直接对函数递归而是迭代。
修改后的代码
using System;
namespace n皇后问题
{
class Program
{
static int Queen_n =12;//皇后数量
static int[] queens = new int[Queen_n];//保存所有皇后的位置
static int QueenSolution_n = 0;//有多少解
static double time = 0;
static void Main(string[] args)
{
time = Environment.TickCount;
for (int i = 0; i < Queen_n; i++)//对所有皇后初始化
{
queens[i] = 0;
}
nQueen(0);
Console.WriteLine(Queen_n + "皇后问题有" + QueenSolution_n + "种解,用时"+(Environment.TickCount-time)+"ms");
Console.ReadKey();
}
static bool IS = false;
static void nQueen(int now)
{
for (int i = now; i < Queen_n; i++)
{
while (IsConlict(i) || queens[i] >= Queen_n)//如果当前皇后的位置与前几个冲突,或者超出棋盘,进来返回上一层
{
queens[i]++;//皇后位置右移
if (queens[i] >= Queen_n)//如果这皇后没有结果
{
if (queens[0] >= Queen_n)//第一个皇后越界,结束
{
return;
}
queens[i] = 0;//当前皇后位置归0
i--;//返回上一个皇后
queens[i]++;//当前皇后位置右移
IS = true;
}
}
if (IS==true)//因为在for后会在++,所以如果是返回上一层需要再减一次
{
i--;
IS = false;
}
if (i == Queen_n - 1)//如果到了第八个皇后,且不冲突。得到一种解
{
queens[i] = 0;//当前皇后位置归0
i--;//返回上一个皇后
queens[i]++;//当前皇后位置右移
QueenSolution_n++;//解+1
i--;
}
}
}
static bool IsConlict(int now)//当前是第now个皇后,一个皇后占一行,所以它是第几个皇后也就表示,这个皇后在第几行
{
for (int i = 0; i < now; i++)
{//在同一对角线,在同一斜对角线,在同一列上
if (((i - now) == (queens[i] - queens[now])) || ((i - now) == -(queens[i] - queens[now])) || (queens[i] == queens[now]))
{
return true;//冲突
}
}
return false;
}
}
}我这种弱鸡毕竟不是ACM选手,也就只能这种程度了。
C++
// n皇后问题c++表示.cpp: 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include
#include
using namespace std;
static int Queen_n = 12;//皇后数量
static int queens[20] = {0};//保存所有皇后的位置
static int QueenSolution_n = 0;//有多少解
bool IsConlict(int now)//当前是第now个皇后,一个皇后占一行,所以它是第几个皇后也就表示,这个皇后在第几行
{
for (int i = 0; i < now; i++)
{//在同一对角线,在同一斜对角线,在同一列上
if (((i - now) == (queens[i] - queens[now])) || ((i - now) == -(queens[i] - queens[now])) || (queens[i] == queens[now]))
{
return true;//冲突
}
}
return false;
}
void nQueen()
{
for (int i = 0; i < Queen_n; i++)
{
while (IsConlict(i) || queens[i] >= Queen_n)//如果当前皇后的位置与前几个冲突,或者超出棋盘,进来返回上一层
{
queens[i]++;//皇后位置右移
if (queens[i] >= Queen_n)//如果这皇后没有结果
{
if (queens[0] >= Queen_n)//第一个皇后越界,结束
{
return;
}
queens[i] = 0;//当前皇后位置归0
i--;//返回上一个皇后
queens[i]++;//当前皇后位置右移
i--;//因为在for后会在++,所以如果是返回上一层需要再减一次
}
}
if (i == Queen_n - 1)//如果到了第八个皇后,且不冲突。得到一种解
{
queens[i] = 0;//当前皇后位置归0
i--;//返回上一个皇后
queens[i]++;//当前皇后位置右移
QueenSolution_n++;//解+1
i--;
}
}
}
int main()
{
double time = clock();
nQueen();
time =clock() - time;
cout << Queen_n << "皇后问题有" << QueenSolution_n << "种解,用时" < python
import time
Queen_n = 8#皇后数量
queens = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]#保存所有皇后的位置
QueenSolution_n = 0#有多少解
def IsConlict(now):#当前是第now个皇后,一个皇后占一行,所以它是第几个皇后也就表示,这个皇后在第几行
for x in range(0,now):#在同一对角线,在同一斜对角线,在同一列上
if (((x - now) == (queens[x] - queens[now])) or ((x - now) == -(queens[x] - queens[now])) or (queens[x] == queens[now])):
return True#冲突
return False
def nQueens():
i=0
while i= Queen_n):
queens[i]+=1
if queens[i]>=Queen_n:
if queens[0]>=Queen_n:#越界结束
return
queens[i]=0
i-=1
queens[i]+=1
i-=1
if i==Queen_n-1:
queens[i]=0
i-=1
queens[i]+=1
global QueenSolution_n
QueenSolution_n+=1
i-=1
i+=1
time0=time.clock()
nQueens()
print(Queen_n, "皇后问题有",QueenSolution_n,"种解,用时" ,int((time.clock()-time0)*1000),"ms")