文件压缩
HuffmanTree
概念
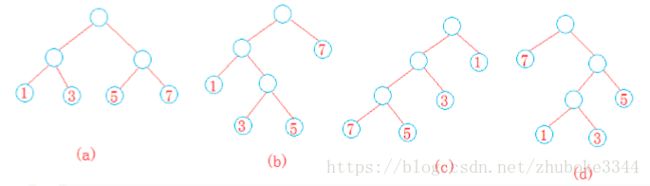
Huffman的定义:假设给定一个有n个权值的集合{w1,w2,w3,…,wn},其中wi>0(1<=i<=n)。若T是一棵有n个 叶结点的二叉树,而且将权值w1,w2,w3…wn分别赋值给T的n个叶结点,则称T是权值为 w1,w2,w3…wn的扩充二叉树。带有权值的叶节点叫着扩充二叉树的外结点,其余不带权值 的分支结点叫做内结点。外结点的带权路径长度为T的根节点到该结点的路径长度与该结点上的权值的乘积。
如上,所有的叶子节点处有所谓的权值,从根结点到某一叶子节点的分支个数为对应的路径长度,如(a)中的权重为1的结点,它的路径长度为2,路径和权值的乘积为2,这颗树的带权路径长度为 1*2 + 3*2 + 5*2 + 7*2 = 32;(b)(c)就不计算了,(d)为7*1 + 1*3 + 3*3 + 5*2 = 29.像(d)这样的带权路径长度最短的树就叫做Huffman树,也叫做最优二叉树。
构造HuffmanTree
1、由给定的n个权值构造n棵只有根节点的二叉树森林。
2、重复一下步骤,直到森林中只有一颗树为止:
- 在森林中选取两棵根节点的权值最小的二叉树,作为左右子树构造一棵新的二叉树。
- 新二叉树的根节点的权值为其左右子树上根节点的权值之和。
- 删除森林中的这两棵树
- 把新的二叉树加入到森林中
void _CreateHuffmanTree(W* array, size_t size, const W& invalid)
{
struct Compare
{
bool operator()(pNode left, pNode right)
{
return left->_weight < right->_weight;
}
Heap hp;
for (size_t i = 0; i < size; i++)
{
if (array[i] != invalid)
hp.Push(new HuffmanTreeNode(array[i]));
}
if (hp.Empty())
_root = NULL;
while (hp.Size() > 1)
{
pNode left = hp.Top();
hp.Pop();
pNode right = hp.Top();
hp.Pop();
pNode pParent = new HuffmanTreeNode(left->_weight);
pParent->_left = left;
left->_parent = pParent;
pParent->_right = right;
right->_parent = pParent;
hp.Push(pParent);
}
_root = hp.Top();
};
} HuffmanTree编码
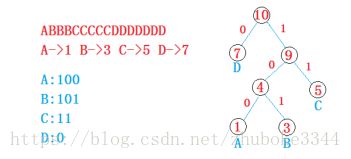
编码:在数据通讯中,将传输的文字转换成二进制字符0和1组成的二进制串的过程。
在不等长编码中,每一个字符编码不能是另一个字符的前缀。
void GetHuffManCode(HuffmanTreeNode* pRoot)//获取Huffman编码
{
if (pRoot)
{
GetHuffManCode(pRoot->_left);
GetHuffManCode(pRoot->_right);
if (NULL == pRoot->_left && NULL == pRoot->_right)
{
HuffmanTreeNode* pCur = pRoot;
HuffmanTreeNode* pParent = pCur->_parent;
string& strCode = _charinfo[pCur->_weight._ch]._strCode;
while (pParent)
{
if (pCur == pParent->_left)
strCode += '0';
else
strCode += '1';
pCur = pParent;
pParent = pCur->_parent;
}
reverse(strCode.begin(), strCode.end());
}
}
} 文件压缩
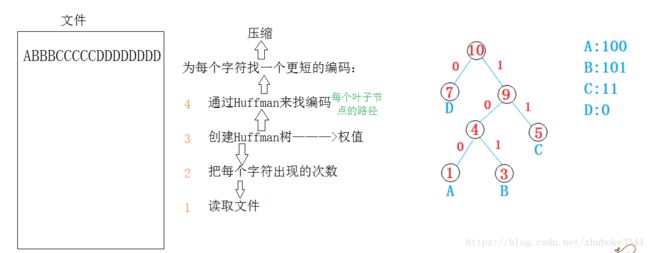
压缩的步骤:
- 读取文件,获取每个字符出现的次数
- 以每个字符出现的次数为权值,创建Huffman树
- 通过Huffman树获取每个字符对应的编码
- 编写压缩文件的头部信息
- 遍历源文件,使用每个字符的新编码重新改写文件
void CompressFile(const string& filepath)//文件压缩
{
//1读取源文件,获取每个字符出现的次数
FILE* fIn = fopen(filepath.c_str(), "r");
if (fIn == NULL)//读取失败
{
cout << "文件路径错误" << endl;
return;
}
char* pReadBuff = new char[1024];
while (true)
{
size_t readsize = fread(pReadBuff, 1, 1024, fIn);
if (readsize == 0)//读取到达文件结尾
break;
for (size_t i = 0; i < readsize; i++)
_charinfo[pReadBuff[i]]._count++;
}
//2以每个字符出现的次数为权值,创建Huffman树
HuffmanTree ht(_charinfo, 256, charInfo(0));
//3通过Huffman树获取每个字符对应的编码
GetHuffManCode(ht.GetRoot());
//写压缩文件的头部信息
string filePostFix = GetFilePostFix(filepath);
string strCodeInfo;
char strCount[32] = { 0 };
size_t LineCount = 0;//记录有效字符的行数
for (size_t i = 0; i < 256; i++)
{
if (_charinfo[i]._count != 0)
{
strCodeInfo += _charinfo[i]._ch;
strCodeInfo += ',';
itoa(_charinfo[i]._count, strCount, 10);
strCodeInfo += strCount;
strCodeInfo += '\n';
LineCount++;
}
}
string strHeadInfo;//压缩文件的头部
strHeadInfo += filePostFix;
strHeadInfo += '\n';
itoa(LineCount, strCount, 10);
strHeadInfo += strCount;
strHeadInfo += '\n';
strHeadInfo += strCodeInfo;
//4用每个字符的编码重新改写文件
FILE* fOut = fopen("2.txt", "w");
assert(fOut);
//压缩编码的信息
fwrite(strHeadInfo.c_str(), 1, strHeadInfo.length(), fOut);
char *pWriteBuff = new char[1024];
char c = 0;
char pos = 0;
size_t writesize = 0;
fseek(fIn, 0, SEEK_SET);//把文件指针重置在起始位置
while (true)
{
size_t readsize = fread(pReadBuff, 1, 1024, fIn);
if (readsize == 0)
break;
for (size_t i = 0; i < readsize; i++)
{
string& strCode = _charinfo[pReadBuff[i]]._strCode;
for (size_t j = 0; j < strCode.size(); j++)
{
c <<= 1;
pos++;
if (strCode[j] == '1')
c |= 1;
if (pos == 8)
{
pWriteBuff[writesize++] = c;
if (writesize == 1024)
{
fwrite(pWriteBuff, 1, 1024, fOut);
writesize = 0;
}
pos = 0;
}
}
}
}
if (pos < 8)//最后一个
{
pWriteBuff[writesize++] = (c << (8 - pos));
}
fwrite(pWriteBuff, 1, writesize, fOut);
fclose(fIn);
fclose(fOut);
delete[] pReadBuff;
delete[] pWriteBuff;
}
压缩后的文件里的内容:
- 源文件的后缀
- 压缩规则的行数
- 压缩规则
- 编码的内容
解压缩的步骤:
- 取出文件头部信息
- 设置字符与对应出现次数
- 以同种算法创建Huffman树
- 解码(编码对应的原字符可由从根结点开始,0走左,1走右,直到遇到叶子节点,则为对应字符)
- 保存
void UnCompressFile(const string filepath)//解压文件
{
FILE* fIn = fopen(filepath.c_str(),"r");
assert(fIn);
//文件后缀
string strFilePostFix;
ReadLine(fIn, strFilePostFix);
//行的次数
string strLineCount;
ReadLine(fIn, strLineCount);
//每个字符出现的次数
size_t linecount = atoi(strLineCount.c_str());
string strCodeInfo;
for (size_t i = 0; i < linecount; i++)
{
strCodeInfo = "";
ReadLine(fIn, strCodeInfo);
_charinfo[strCodeInfo[0]]._count = atoi(strCodeInfo.c_str() + 2);
}
//还原Huffman树
HuffmanTree ht(_charinfo, 256, charInfo(0));
string compressfilepath = GetFilePath(filepath);
compressfilepath += strFilePostFix;
FILE* fOut = fopen(compressfilepath.c_str(), "w");
assert(fOut);
//解压缩
char* pReadBuff = new char[1024];
char* pWriteBuff = new char[1024];
size_t writesize = 0;
size_t pos = 8;
HuffmanTreeNode *pCur = ht.GetRoot();
size_t filesize = pCur->_weight._count;//文件的总大小
while (true)
{
size_t readsize = fread(pReadBuff, 1, 1024, fIn);
if (readsize == 0)//到达文件结尾
break;
for (size_t i = 0; i < readsize; i++)
{
pos = 8;
while (pos--)
{
if (pReadBuff[i] & 1 << pos)//字符为1,朝右子树走
pCur = pCur->_right;
else//字符为0,朝左子树走
pCur = pCur->_left;
if (pCur->_left == NULL && pCur->_right == NULL)//到达叶子节点
{
pWriteBuff[writesize++] = pCur->_weight._ch;
if (writesize == 1024)//写满了
{
fwrite(pWriteBuff, 1, 1024, fOut);
writesize = 0;
}
if (--filesize == 0)//解压完了
{
fwrite(pWriteBuff, 1, writesize, fOut);
break;
}
pCur = ht.GetRoot();//pCur回到根节点
}
}
}
}
delete[] pReadBuff;
delete[] pWriteBuff;
fclose(fIn);
fclose(fOut);
} 效果