数据结构课程设计(一)---24点
一、计算24点
1、任务简述:
一副扑克牌的每张牌表示一个数(J、Q、K分别表示11、12、13,两个司令不用)。任取4张牌,即得到1-13的数,请添加运算符(规定为加、减、乘、除四种)使之成为运算式。每个数只能参与一次运算,4个数顺序可以任意组合,4个运算符任意取3个且可以重复取。运算遵从一定有限级别,可加括号控制,最终使运算结果为24.请输出一种解决方案的表达式,用括号表示运算优先。如果没有解决方案,则输出-1表示无解。
要求:
(1)输入说明:输入采用随机生成4个整数,每个整数取值范围是[1, 13].
(2)输出说明:输出一种解决方案的表达式,用括号表示运算优先,如果没有解决方案,则输出-1。
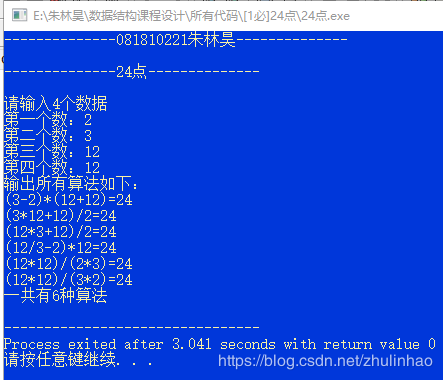
(3)测试用例: 输入 2 3 12 12 输出 ((3-2)*12)+12
(4)可选要求:输出要求输出该4个整数所有可能的解决方案。
2、算法描述:
采用思维上最简单的方法,就是遍历所有可能性,如果可以算出24就输出,并且让变量flag++来记录算法个数,如果flag是0,则输出-1,表示这四个数字无法算出24点。我的代码中必要有优势的去重的方法为check函数,这个函数是针对输入的数据a,b,c,d进行处理,找出他们之中相同的个数,一共有五种情况:1.都不相同,那么不做调整;2.有且仅有两个相同,那么把相应的相同的元素放在c和d 的位置;3.有两组数字分别相同(比如a=c,b=d,但是a,b不等),那么把相同的放在一起;4.有三个相同,那么把他们发在b,c,d的位置;5.全部相同,那么不做调整。根据不同的情况,去遍历所有的可能性,一来成功去重,二来减少了运算的次数(就是比如:2,3,12,12可以认为第一个12只会在第二个之前)。

3、源代码
#include 4、运行结果
1.测试1:2,3,12,12:
2.测试2:1,2,2,3
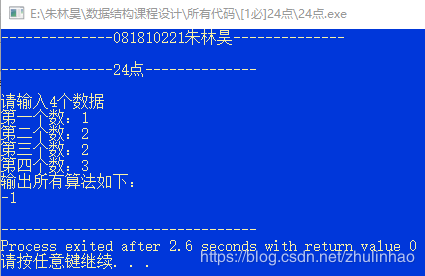
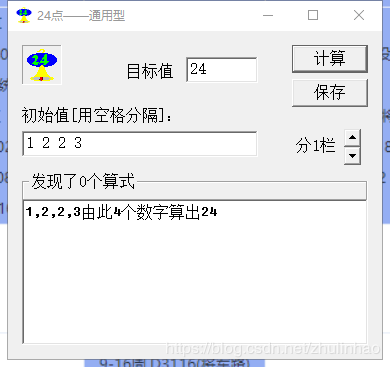
我们发现是没有相应的运算式的,可以验证:
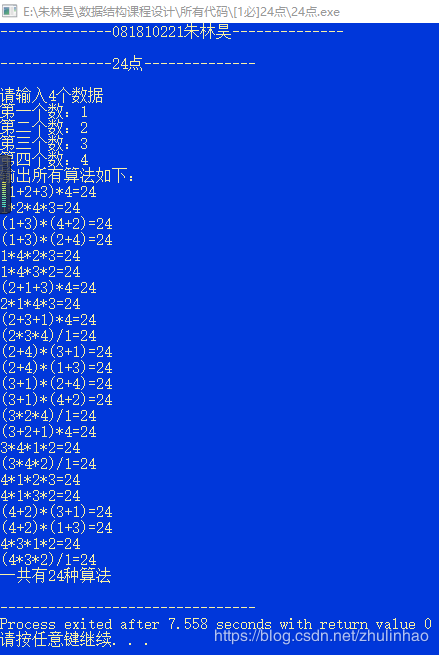
3.测试3:1,2,3,4
4.输入非法数据
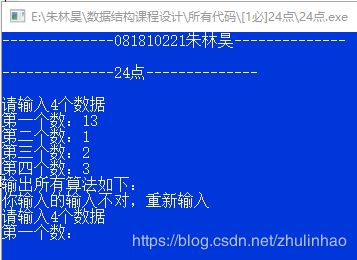
并且由于我加了一个m_ret: 来做标记,可以返回重新输入。
5、总结
性能分析:
时间复杂度:因为最坏情况下随机序列(此时四个数字完全不同)的全排列个数是有限的,为4!3!种排列结果,因此时间复杂度O©
空间复杂度:O©
遇到的问题与解决方法:
容易出现表达式重复的现象,所以为了在一定程度上减少重复输出,所以我采用了对原始数据进行了一个简单的预处理,具体方法思路如上,这里就不做赘述了。
心得体会:
从结果上来看,程序代码是正确的,但是虽然长得完全一样的表达式是不会出现了,但是也只能做到这个最基本的判重,对于比如:2+3和3+2,我写的代码还是认为他们是不一样的,但在实际中,他们应该是一样的,即应该去重,不过这个实现较为困难,虽然有思路——可以采用排序和字符串比较来实现,但是那样代码长度会太长,所以只实现到了这样。
我感觉我对于数据的原始处理是写的不错的,可以根据数据的不同特征,做出不同的处理方式,一旦相同的原始,那么处理步数就会减少,那么效率就提高了。并且我可以统计出算24点的方法的数量并给出。
存在问题和改进方法:
即使我对数据进行了预处理,保证不可能出现完全一样的表达式,但是由于+和具有交换性,所以,其实2+1和1+2应该认为是等价的,即是相同的表达式,但是由于篇幅问题,我没有展开来处理,但是我有以下思路来进行处理:思路①:用二叉树的结构,叶子节点放带计算的数字,然后他们的父节点先放运算符,然后用计算后的值替换,所以当某两个数字共同的父节点是+或者x时,我们可以交换左右孩子的值,看此时父节点算出来的值是否一样,如果一样就可以只输出其中某一个。思路①:和上面大致相同,但是对左右孩子的值做一个要求,即对于父节点是+或者x的,右孩子的值要大于等于左孩子的值,这样也可以做到去重。