数据结构课程设计（十）---迷宫问题

1、任务简述：
设计非递归算法，根据入口和出口位置将给定迷宫中的全部可行路线输出，并标记出其中的最短路径；

int mg[10][10]={
	{1,1,1,1,1,1,1,1,1,1},
	{1,0,0,1,0,0,0,1,0,1},
	{1,0,0,1,0,0,0,1,0,1},
	{1,0,0,0,0,1,1,0,0,1},
	{1,0,1,1,1,0,0,0,0,1},
	{1,0,0,0,1,0,0,0,0,1},
	{1,0,1,0,0,0,1,0,0,1},
	{1,0,1,1,1,0,1,1,0,1},
	{1,1,0,0,0,0,0,0,0,1},
	{1,1,1,1,1,1,1,1,1,1},	
};	//该二维数组表示迷宫，0表示可行，1表示不可行。

要求：
（1）提示用户从键盘输入入口位置和出口位置；
（2）输出所有可行路线及其路径长度（路径中包含的点的个数），并标记出其中的最短路径（最短路径可能有一条或者若干条）
（3）如果入口与出口之间不存在路径，也请给出相应的提示信息；

2、算法描述：
首先用宽搜来寻找最短路径的长度，然后用深搜来找出所有路径，并且标记出其中的最短的路径。其中宽搜采用的是队列，深搜采用的是栈。思路都是去寻找可以走的几个方向，逐个判断就行了。

3、源代码：

#include
#include
#include
#define N 100
int mg[10][10]={
	{1,1,1,1,1,1,1,1,1,1},
	{1,0,0,1,0,0,0,1,0,1},
	{1,0,0,1,0,0,0,1,0,1},
	{1,0,0,0,0,1,1,0,0,1},
	{1,0,1,1,1,0,0,0,0,1},
	{1,0,0,0,1,0,0,0,0,1},
	{1,0,1,0,0,0,1,0,0,1},
	{1,0,1,1,1,0,1,1,0,1},
	{1,1,0,0,0,0,0,0,0,1},
	{1,1,1,1,1,1,1,1,1,1},	
};	//该二维数组表示迷宫，0表示可行，1表示不可行。
int flag[10][10]={
	{1,1,1,1,1,1,1,1,1,1},
	{1,0,0,1,0,0,0,1,0,1},
	{1,0,0,1,0,0,0,1,0,1},
	{1,0,0,0,0,1,1,0,0,1},
	{1,0,1,1,1,0,0,0,0,1},
	{1,0,0,0,1,0,0,0,0,1},
	{1,0,1,0,0,0,1,0,0,1},
	{1,0,1,1,1,0,1,1,0,1},
	{1,1,0,0,0,0,0,0,0,1},
	{1,1,1,1,1,1,1,1,1,1},	
};	//该二维数组表示迷宫，0表示可行，1表示不可行。

int ms[4][2] = {{-1,0},{1,0},{0,1},{0,-1}};

int BFS(int start_x,int start_y,int end_x,int end_y);//宽度优先搜索，寻找最短路径，并且返回他最短路径的节点个数。 
void DFS(int k,int start_x,int start_y,int end_x,int end_y);//深度优先搜索，寻找所有可行路径 
main()
{
	int start_x,start_y,end_x,end_y;    //迷宫的起点和终点 
	int k;   //最短路径的节点个数
	printf("请输入迷宫的起点坐标x,y: ");
	scanf("%d %d",&start_x,&start_y);
	printf("请输入迷宫的终点坐标x,y: ");
	scanf("%d %d",&end_x,&end_y);
	k = BFS(start_x,start_y,end_x,end_y);
	if(k!=0)
		DFS(k,start_x,start_y,end_x,end_y);
	else
		printf("该迷宫没有出去的路线!");
}

int BFS(int start_x,int start_y,int end_x,int end_y) //宽度优先搜索，寻找最短路径，并且返回他最短路径的节点个数。
{
	int x[N],y[N],front[N],rear,head;
	int dir,flag = 0,temp,sum = 0;
	int cx,cy,nx,ny;
	head = rear = 0;
	x[0] = start_x;
	y[0] = start_y;
	front[0] = -1;
	mg[start_x][start_y] = 1;
	while(head <= rear)
	{
		cx = x[head];
		cy = y[head];
		for(dir = 0;dir<4;dir++)
		{
			nx = cx+ms[dir][0];
			ny = cy+ms[dir][1];
			if(mg[nx][ny] ==0)
			{
				rear++;
				x[rear] = nx;
				y[rear] = ny;
				front[rear] = head;
				mg[nx][ny] = 1;
			}
			if(nx == end_x&&ny == end_y)
			{
				flag = 1;
				break;
			}
		}
		if(flag == 1)
			break;
		head++;
	}
	if(flag == 1)
	{
		for(temp = rear;temp >= 0;temp = front[temp])
			sum++;
		return sum;
	}
	else
		return 0;
}

void DFS(int k,int start_x,int start_y,int end_x,int end_y)//深度优先搜索，寻找所有可行路径 
{
	int x[N],y[N],dir[N],top;
	int i,sum=0,count;
	int cx,cy,nx,ny;
	top = 0;
	x[0] = start_x;
	y[0] = start_y;
	dir[0] = 0;
	flag[start_x][start_y] = 1;
	while(top>=0)
	{
		cx = x[top];
		cy = y[top];
		if(cx==end_x&&cy==end_y)
		{
			sum++;
			if(top+1 == k)
				printf("----------最短路径为下面这条--------------：\n");
			count = 0;
			printf("方案%d :",sum);
			for(i = 0;i<=top;i++)
			{
				count++;
				printf("(%d,%d) ",x[i],y[i]);
			}
			printf("---有%d个节点\n\n",count);
			top--;
			flag[cx][cy] = 0;
			continue;
		}
		if(dir[top] == 4)
		{
			top--;
			flag[cx][cy] = 0;
			continue;
		}
		nx = cx + ms[dir[top]][0];
		ny = cy + ms[dir[top]][1];
		dir[top]++;
		if(flag[nx][ny]==0)
		{
			top++;
			x[top] = nx;
			y[top] = ny;
			flag[nx][ny] = 1;
			dir[top] = 0;
		}
	}
	printf("一共有%d种走法",sum);
}//145行

4、运行结果
起点为：（1，1）,终点为：（8，8）



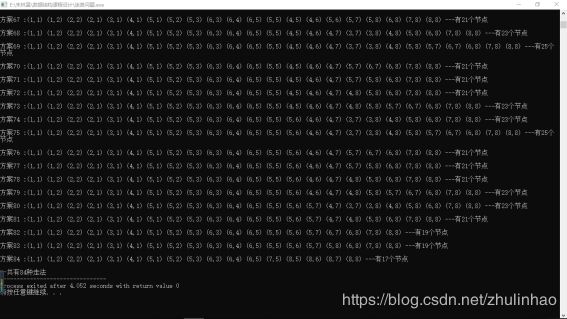
由于迷宫中任意两个点都是联通的，我们修改了一下迷宫：
int mg[10][10]={
{1,1,1,1,1,1,1,1,1,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,0,0,1,1,0,0,1},
{1,0,1,1,1,0,0,0,0,1},
{1,0,0,0,1,0,0,0,0,1},
{1,0,1,0,0,0,1,0,0,1},
{1,0,1,1,1,0,1,1,0,1},
{1,1,0,0,0,1,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1},
}; //该二维数组表示迷宫，0表示可行，1表示不可行。
然后寻找起点：（1，1），终点：（8，2）：

5、总结
心得体会：
运行结果正确，输出也是正序输出，成功统计路径数量，不过可以学习老师的system(“pause”)，就是每输出10个或20个停一下，再输出。不过这个影响不大。