电路课组(一)电路原理 Part 3 电阻和电源的等效变换
文章目录
- 求解方法综述
- 1. 电阻的串并联规律
- 1.1. 串联
- 1.2. 并联
- 1.3. 串并联简化方法( ∗ \ast ∗)
- 2. 电桥和平衡电桥
- 3. Y − Δ Y-\Delta Y−Δ(星-三角变换):三角形网络
- 3.1. Y − T Y-T Y−T和 Δ − Π \Delta-\Pi Δ−Π形
- 3.2. 等效条件
- 3.2.1. Y → Δ Y\to\Delta Y→Δ:星接转角接
- 3.2.2. Δ → Y \Delta\to Y Δ→Y:角接转星接
- 3.3. 应用:求解电桥电路( ∗ \ast ∗)
- 4. 电源等效
- 4.1. 带受控源的网络阻值求解——加压求流和加流求压
- 4.2. 理想独立源的串并联
- 4.2.1. 独立源的串联
- 独立电压源串联
- 独立电压源和独立电流源串联
- 4.2.2. 独立源的并联
- 独立电流源的并联
- 独立电压源和独立电流源的串联
- 4.3. 实际独立源的等效变换
- 判断含源网络是否等效( ∗ \ast ∗)
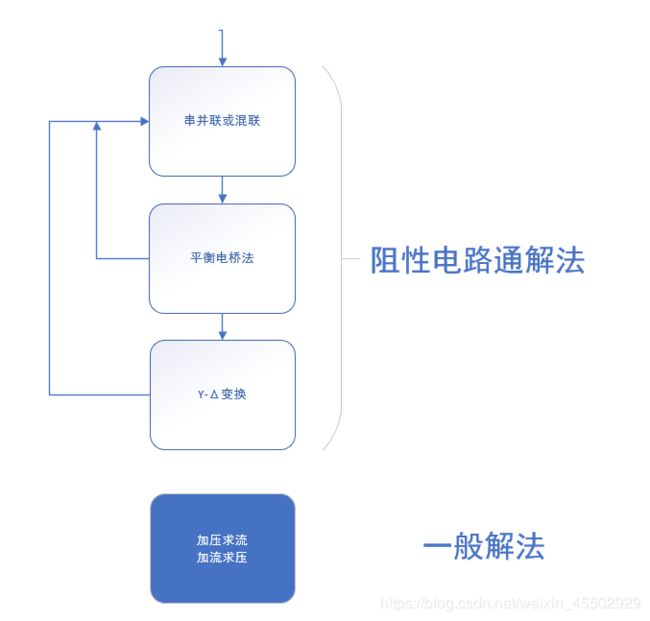
求解方法综述
电路分析中有很多典型而简单的分析方法,比如混联电路的分析、平衡电桥。但同时我们发现很多问题是不能简单地进行求解的,所以我们还要讨论一些网络等效的方法,包括网络的等效、电源等效,etc。
1. 电阻的串并联规律
1.1. 串联
对串联回路使用KVL,得到串联电阻的阻值:
R s = ∑ R i R_s=\sum R_i Rs=∑Ri
由Ohm定律,串联分压规律:
U i R i = U s R s \frac{U_i}{R_i}=\frac{U_s}{R_s} RiUi=RsUs
- 对于一个非独立电压源,考虑电路中串入一个内电阻。由分压规律,这个电阻越小,那么负载电压越大。
1.2. 并联
对并联节点使用KCL,可得并联的电导:
G p = ∑ G k G_p=\sum G_k Gp=∑Gk
由电导的Ohm定律,并联分流规律:
i k i = G k G p \frac{i_k}{i}=\frac{G_k}{G_p} iik=GpGk
- 特别地,对于两个支路并联,支路电流占总电流比重等于对侧电阻占阻值之和的比重。
- 对一个非独立电流源,考虑电路中并入一个内电阻。由分流规律,这个电阻越大,那么负载电流越大。
1.3. 串并联简化方法( ∗ \ast ∗)
寻找直接串联或者并联在电源上的网络部分
这样的部分是一定存在的,只要是一个混连电路,最外层结构必然是一个串联或一个并联。
对其进行移动节点,或删除简化。对于一个确定的串并联混合电路,都可以通过这样的方法逐步实现问题的解析。
例题 求这个串并联网络的电阻:
- step 1:0.6串联
- step 2:6并联
- step 3:右边的4串联
- step 4:左边的4和2并联
2. 电桥和平衡电桥
由分压规律
U A = R 2 R 1 + R 2 U_A=\frac{R_2}{R_1+R_2} UA=R1+R2R2
U B = R 4 R 3 + R 4 U_B=\frac{R_4}{R_3+R_4} UB=R3+R4R4
如果 R 1 R 4 = R 2 R 3 R_1R_4=R_2R_3 R1R4=R2R3,那么AB两点是等电位点。从而中间连入的电阻没有电流通过。因而这个平衡电桥简化为简单的串并联结构。
平衡电桥可以认为是并联的串联,也可以看成串联的并联。
3. Y − Δ Y-\Delta Y−Δ(星-三角变换):三角形网络
3.1. Y − T Y-T Y−T和 Δ − Π \Delta-\Pi Δ−Π形
前者是三分岔(把线路垂直画出来就是T形),后者是在中间有一个回路(把线路垂直画出来,空出一条边就是 Π \Pi Π形)。


3.2. 等效条件
经过一系列解方程,可以得到两种网络互相等效的条件。
助记法:
Y形几条代三角一条边,所以阻值小。转化为三角形时是相加。
三角形相反,转化为Y形是合起来相除。
3.2.1. Y → Δ Y\to\Delta Y→Δ:星接转角接
下标对应阻值相加+下标对应阻值相乘除以对边阻值
{ R 12 = R 1 + R 2 + R 1 R 2 R 3 R 23 = R 2 + R 3 + R 2 R 3 R 1 R 31 = R 3 + R 1 + R 3 R 1 R 2 \begin{cases} R_{12}=R_1+R_2+\frac{R_1R_2}{R_3}\\ R_{23}=R_2+R_3+\frac{R_2R_3}{R_1}\\ R_{31}=R_3+R_1+\frac{R_3R_1}{R_2} \end{cases} ⎩⎪⎨⎪⎧R12=R1+R2+R3R1R2R23=R2+R3+R1R2R3R31=R3+R1+R2R3R1
3.2.2. Δ → Y \Delta\to Y Δ→Y:角接转星接
下标存在的两个阻值相乘除以总阻值
{ R 1 = R 12 R 31 R 12 + R 23 + R 31 R 2 = R 23 R 12 R 12 + R 23 + R 31 R 3 = R 31 R 23 R 12 + R 23 + R 31 \begin{cases} R_1=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}\\ R_2=\frac{R_{23}R_{12}}{R_{12}+R_{23}+R_{31}}\\ R_3=\frac{R_{31}R_{23}}{R_{12}+R_{23}+R_{31}} \end{cases} ⎩⎪⎨⎪⎧R1=R12+R23+R31R12R31R2=R12+R23+R31R23R12R3=R12+R23+R31R31R23
3.3. 应用:求解电桥电路( ∗ \ast ∗)
对于不能平衡的电桥,我们可以考虑将其中部分已知的三端网络进行 Y − Δ Y-\Delta Y−Δ变换。随后化成可解的问题。

这个图中,1kΩ的四个电阻构成一个 Δ \Delta Δ形(红框)和Y形(绿框)网络。
分别对应将其化为星接和角接如下:

红框中三个电阻都为1/3kΩ。
星接转角接:
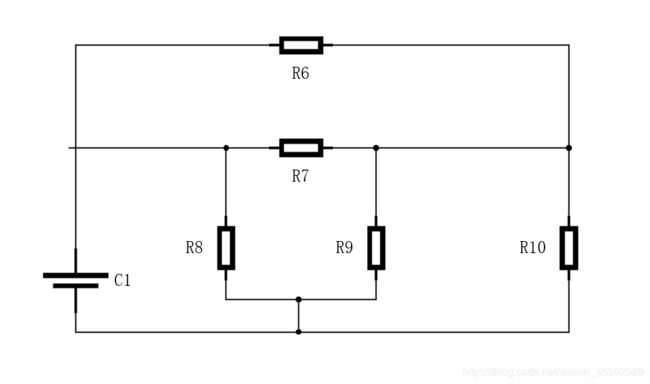
此为一个电阻 R 8 R_8 R8并联一个平衡电桥。
4. 电源等效
4.1. 带受控源的网络阻值求解——加压求流和加流求压
使用“加压求流”和“加流求压”法。
这个方法的名字实际上是一句废话 就表明此方法的通解性。因为它体现了网络抽象+欧姆定律的综合使用的本质属性。相当于是定义法,即:
U = I ∗ □ I = U / □ U=I*\Box\\ I=U/\Box U=I∗□I=U/□
这个思路也支持带有受控源的网络。
4.2. 理想独立源的串并联
首先要说明一点,就是独立源具有和我们的理想电路模型有等效对应。
- 独立电流源相当于无限大电阻,或断路
- 独立电压源相当于导线,或短路。
它们二者所提供的电压、电流可以认为是这两种理想模型的附加属性。
也就是说,独立电流源是一个“电流确定的断路支路”,独立电压源是一个“电压确定的导线”
4.2.1. 独立源的串联
独立电压源串联
独立电压源 U S 1 , U S 2 ⋯ U S n U_{S1}, U_{S2}\cdots U_{Sn} US1,US2⋯USn串联,仍然相当于一条导线,其上短通性质并不改变,仍然为独立源。又由KVL可得其独立电压为 ∑ U S i \sum U_{Si} ∑USi。
独立电压源和独立电流源串联
串联支路中,一断则断。因而性质等同于断路,为一个独立电流源
因为电压源的外电流已经因为电流源而确定
所以相当于对外性质没有变化的独立电流源。
另外,独立电压源在这里就相当于一个虚拟电阻,可以分担提供一部分电压,所以原来的独立电流源上电压会减小。
这个电压也是独立电压源唯一的作用。
4.2.2. 独立源的并联
独立电流源的并联
多个断路并在一起仍然不能导通,所以仍然是独立电流源。由KCL得 I 1 , I 2 ⋯ I n I_1,I_2\cdots I_n I1,I2⋯In
独立电压源和独立电流源的串联
并联中只要一个支路为短路,一短则短。故为电压源,并入一个电流源后端口性质不变。同样地,电流源的目的是提供一部分电流,电压源的电流减小。
但是,在这里电流源并不能相当于一个支路,因为其方向和电压源所能提供的电流方向是相反的。
4.3. 实际独立源的等效变换
实际独立电压源和电流源
u = U s − R s i i = I s − G s u u=U_s-R_si\\ i=I_s-G_su u=Us−Rsii=Is−Gsu
对比系数可得等效条件:
{ U s = I s ′ R s R s = R s ′ \begin{cases} U_s=I_s'R_s\\ R_s=R_s' \end{cases} {Us=Is′RsRs=Rs′
含义:
- I s I_s Is为电流源电流, U s U_s Us为电压源电压, R s R_s Rs为待转化电源的内阻。
- 它们的“内阻”(对于电压源来说是串联,电流源是并联)相等。
关于这种源等效的可行性:
- 实际独立电压源:随电流增大而电压被分走。
- 实际独立电流源:随电压增大而电流被分走。
也就是说,两种源的电流电压均呈线性负相关,尽管内部的改变机理不同,仍然奇妙地实现了相同的结果。
判断含源网络是否等效( ∗ \ast ∗)
- 删掉无效元件:串入电阻(电压源)对电流源没有影响,并入电阻(电流源)对电压源没有影响。
- 串并联操作:电源串联先转化成实际电压源结构。电源并联先转化成实际电流源结构。受控源也可以进行类似独立源的操作。
- 退字诀:复杂的情况还是要回到最初的伏安特性上去。
比如通过伏安特性我们就能验证,左边的支路就等效于一个电流源。
这和电流源串电压源的想法是一致的。因此我们最开始将串入的电压视作虚拟电阻是可行的。对总阻值没有影响,仅有的效果是分压。


